python 因子分析

目录

一、算法作用

二、案例

1、关于数据

2、数据标准化

3、适用性检验

3.1 KMO和Bartlett球形检验

4、因子提取

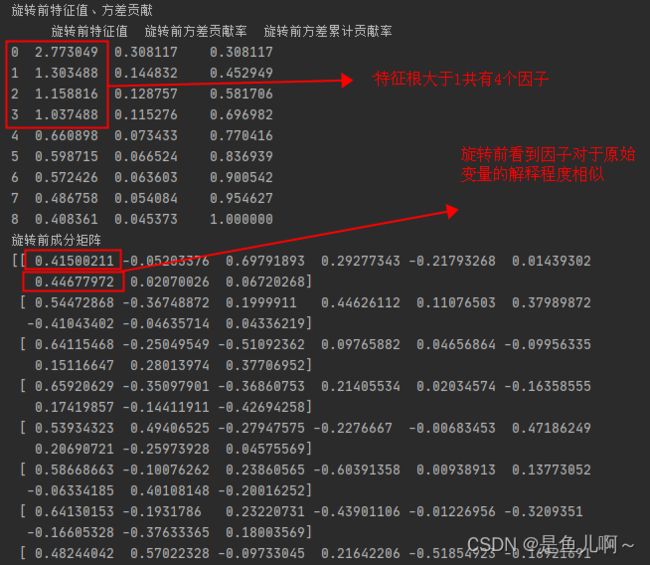
4.1 数据原始特征值、方差贡献率

5 因子旋转

6 因子命名

7 因子得分

---

一、算法作用

1、剔除相关性和降维：因子分析主要是根据相关性大小大小把原始变量分组，使得组内的变量间相关性较高，不同的组变量间的相关性较低，通过将原始变量提取出少量的公共因子，通过少量的公共因子来解释原来多变量代表的问题。

2、对变量或样本分类处理：在得出因子的表达式之后，可以把原始变量的数据代入表达式得出因子得分值，根据因子得分在因子所构成的空间达到分类的目的。

二、案例

1、关于数据

本次案例使用的数据来自陈哲老师《活用数据》STP分析案例解释中的部分数据，数据在

博文python因子分析中使用的数据-数据集文档类资源-CSDN下载

数据是来源于对客户生活状态9个方面的问题调查统计数据，9个问题之间从问题描述看可能存在相关性，数据之间存在相关性会造成重叠信息扩大化，增加分类的偏差，因此需要剔除语句之间的相关，剔除的方法就是本文要使用的因子分析。

读入数据

import pandas as pd 
file = "data_of_life_atitude.xlsx"
f= pd.read_excel(file,header=1)#从第二行开始读数据，因为第一行是变量名称不能进行标准化

2、数据标准化

在处理数据之前一般会对数据进行预处理，将不同规格的数据转换到同一规格，使用的最多的方式是Z分数标准化，即减去均值除以方差的方式。在python中可以直接调用StandarScaler

from sklearn.preprocessing import StandardScaler
data = StandardScaler().fit_transform(data) 

3、适用性检验

适用性检验主要是检验数据是否可以使用因子分析，因为因子分析的前提是原始维度之间具有相关性，因此适用性检验就是检验原始维度之间是否具有相关性，如果不相关则不适合做因子分析。

3.1 KMO和Bartlett球形检验

主要用的到的方法是KMO和Bartlett球形检验，其中Bartlett球形检验用于检验变量之间是否相关独立，如果p值小于0.05则适合做因子分析；

KMO用于检验变量之间的相关性取值在0-1之间，值越大相关性越强。

可以直接在python因子库中调用，使用之前需要先安装对应的库。

from factor_analyzer import FactorAnalyzer, calculate_kmo, calculate_bartlett_sphericity
kmo = calculate_kmo(f)
bartlett = calculate_bartlett_sphericity(f)
if kmo[1] >= 0.7 and bartlett[1] <= 0.05:  # bartlett球形度检验p值要小于0.05 kmo值要大于0.7
    print("\n因子分析适用性检验通过\n")
else:
    print("\n因子分析适用性检验未通过\n")
print('kmo:{},bartlett:{}'.format(kmo[1], bartlett[1]))

#kmo:0.7151496149882955,bartlett:2.1981583743078605e-220

将kmo大于0.7且通过Bartlett检验的情况设置为通过适度性检验，本案例通过因子适度性检验。

4、因子提取

4.1 数据原始特征值、方差贡献率

因子提取主要看特征根和解释的总方差

Load_Matrix = FactorAnalyzer(rotation=None, n_factors=len(f.T), method='principal')
Load_Matrix.fit(f)
f_contribution_var = Load_Matrix.get_factor_variance()
matrices_var = pd.DataFrame()
matrices_var["旋转前特征值"] = f_contribution_var[0]
matrices_var["旋转前方差贡献率"] = f_contribution_var[1]
matrices_var["旋转前方差累计贡献率"] = f_contribution_var[2]
print(matrices_var)#旋转前的特征值、方差贡献等
print(Load_Matrix.loadings_)#旋转前的成分矩阵

共因子个数选择，对于公因子的个数选择一般会按照特征根大于1的标准或者累计贡献率设置一个值，本文使用前者作为参考：

eigenvalues = 1
N = 0
for c in matrices_var["旋转前特征值"]:
    if c >= eigenvalues:
        N += 1
    else:
        s = matrices_var["旋转前方差累计贡献率"][N-1]
        print("\n选择了" + str(N) + "个因子累计贡献率为" + str(s)+"\n")
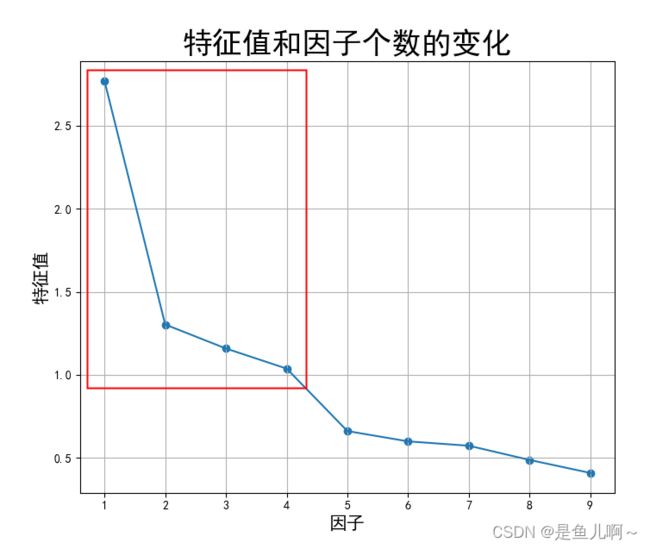
        break

对于特征根还可以画图参考，这个图好像作用不太大，主要可能更加直观。一般因子提取的方式是使用主成分分析的方法。

import matplotlib
matplotlib.rcParams["font.family"] = "SimHei"  # 主要用来看取多少因子合适，一般是取到平滑处左右，当然还要需要结合贡献率
ev, v = Load_Matrix.get_eigenvalues()
print('\n相关矩阵特征值：', ev)
plt.figure(figsize=(8, 6.5))
plt.scatter(range(1, f.shape[1] + 1), ev)
plt.plot(range(1, f.shape[1] + 1), ev)
plt.title('特征值和因子个数的变化', fontdict={'weight': 'normal', 'size': 25})
plt.xlabel('因子', fontdict={'weight': 'normal', 'size': 15})
plt.ylabel('特征值', fontdict={'weight': 'normal', 'size': 15})
plt.grid()
plt.show()

 通过以上输出的结果可以看出，原始因子之间存在相关性，因子之间没有差异化特征，所以需要进行因子旋转。

5 因子旋转

目的：使得各因子具有差异化的特征；

使用方法：最大方差法（正交旋转）、斜交旋转（多使用前者）

Load_Matrix_rotated = FactorAnalyzer(rotation='varimax', n_factors=N, method='principal')
Load_Matrix_rotated.fit(f)

查看旋转后成分矩阵以及特征根方差贡献

f_contribution_var_rotated = Load_Matrix_rotated.get_factor_variance()
matrices_var_rotated = pd.DataFrame()
matrices_var_rotated["特征值"] = f_contribution_var_rotated[0]
matrices_var_rotated["方差贡献率"] = f_contribution_var_rotated[1]
matrices_var_rotated["方差累计贡献率"] = f_contribution_var_rotated[2]
print("旋转后的载荷矩阵的贡献率")
print(matrices_var_rotated)
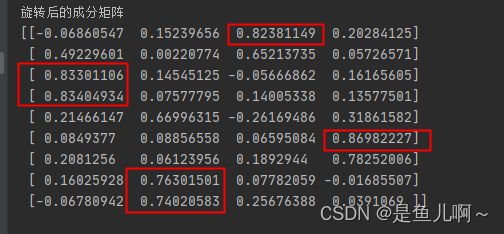
print("旋转后的成分矩阵")
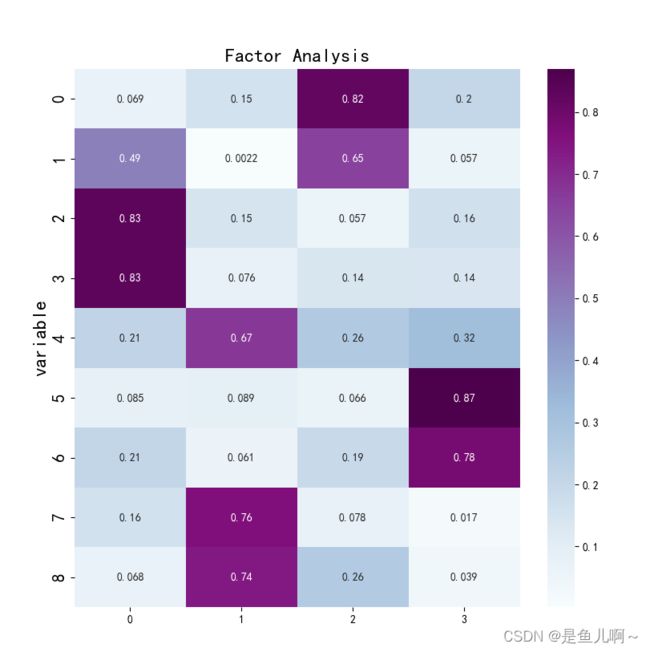
print(Load_Matrix_rotated.loadings_)

 可以看见成分矩阵中只有一个因子表示变量的值比较大，相关性降低，为了直观这里可以画一个相关性图形。

import seaborn as sns
Load_Matrix = Load_Matrix_rotated.loadings_
df = pd.DataFrame(np.abs(Load_Matrix),index= f.columns)

plt.figure(figsize=(14, 14))
ax = sns.heatmap(df, annot=True, cmap="BuPu")
ax.yaxis.set_tick_params(labelsize=15) # 设置y轴字体大小
plt.title("Factor Analysis", fontsize="xx-large")
plt.ylabel("variable", fontsize="xx-large")# 设置y轴标签
plt.show()# 显示图片

6 因子命名

在旋转后的成分矩阵中，可以看到因子1主要反应2、3个变量中特征，对应的变量可以在原始数据中查看分别为“买房子前先有车”（0.833）以及“不惜金钱和时间装修房子”（0.835）因子可以把这个因子命名为“享受型因子”；其他因子可以类似命名

7 因子得分

当因子模型建立后，需要反过来考察一个样品的性质以及样品之间的相互关系，比如当关于企业经济效益的因子模型建立之后，希望知道每一个企业经济效益的优劣，或者把企业进行分类，这个时候就需要进行因子得分计算。

# 计算因子得分（回归方法）（系数矩阵的逆乘以因子载荷矩阵）
f_corr = f.corr()# 皮尔逊相关系数
X1 = np.mat(f_corr)
X1 = nlg.inv(X1)
factor_score_weight = np.dot(X1, Load_Matrix_rotated.loadings_)
factor_score_weight = pd.DataFrame(factor_score_weight)
col = []
for i in range(N):
    col.append("factor" + str(i + 1))
factor_score_weight.columns = col
factor_score_weight.index = f_corr.columns
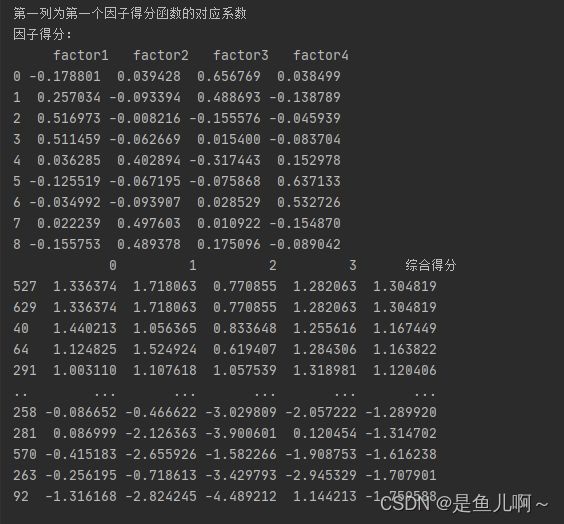
print("\n第一列为第一个因子得分函数的对应系数")
print("因子得分：\n", factor_score_weight)

factor_score = pd.DataFrame(np.dot(np.mat(f), np.mat(factor_score_weight)))  # 指标 * 对应权重，计算出因子的分数

i = 0
factor_score["综合得分"] = 0
for factor_score_weight in matrices_var_rotated["方差贡献率"]:
    factor_score["综合得分"] += factor_score_weight * factor_score[i]  # 因子贡献率 * 因子的分数 用于计算综合得分
    i += 1
    if i == N:
        break
factor_score["综合得分"] = factor_score["综合得分"] / matrices_var_rotated["方差贡献率"].sum()  # 计算综合得分
print(factor_score.sort_values(by=["综合得分"], ascending=False))  # 排个序

 其中综合得分一般用于在对应权重后选择靠前后者综合排名靠后的数

同样可以使用因子得分来对数据进行分类，在数据中把在因子得分中最高的得分因子提取出来，比如编号是527的数据得分最高的是因子1，因此为因子的特征，以此来进行数据分类。