R语言数值导数
文章目录
-
- 3 数值导数
3 数值导数
根据导数的定义,当函数的定义域不连续时,其不连续处显然是不存在导数的,但图形可以“欺骗”我们的眼睛。
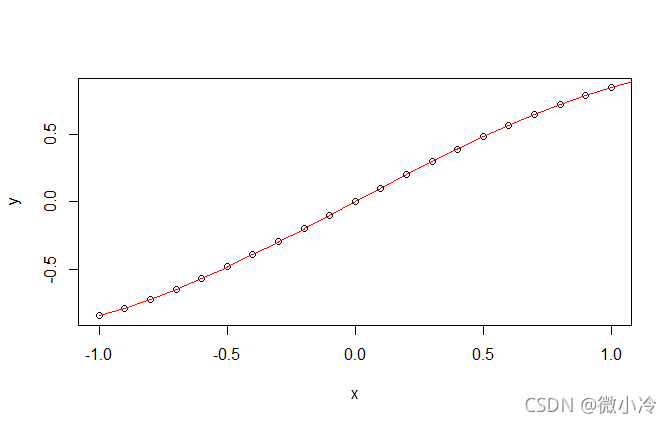
> x = seq(-1,1,0.1)
> y = sin(x)
> y1 = cos(x)
> xEnd = x+0.1
> yEnd = y+y1*0.1
> plot(x,y)
> for(i in seq_along(x)){
+ lines(c(x[i],xEnd[i]),c(y[i],yEnd[i]),col="red")
+ }
上图中,圆圈是对 y = sin x y=\sin x y=sinx进行抽样的结果,可以理解为是一个不连续的函数;红线则是在每一个分立的点上, sin x \sin x sinx在该点的切线。这两者看上去如此一致,说明连续函数的导数在抽样之后仍然具备一定的数学意义。
相应地,不连续的函数,也应该有类似于导数一样的存在,从而与连续函数的导数相对应,此即数值导数。如果回顾导数的定义
f ′ ( x 0 ) = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x f'(x_0)=\lim_{\Delta x\to0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} f′(x0)=Δx→0limΔxf(x0+Δx)−f(x0)
当 Δ x ↛ 0 \Delta x\not\to 0 Δx→0时,即可理解为数值导数。
假设现在对某个函数 f ( x ) f(x) f(x)进行等间隔抽样,间隔为 h h h,则其第 n n n个点处的数值导数为
f [ x n ] = f ( x n + 1 ) − f ( x n ) x n + 1 − x n = f ( x n + h ) − f ( x n ) h f[x_n]=\frac{f(x_{n+1})-f(x_n)}{x_{n+1}-x_n}= \frac{f(x_n+h)-f(x_n)}{h} f[xn]=xn+1−xnf(xn+1)−f(xn)=hf(xn+h)−f(xn)
由于一般称 f ( x n + 1 ) − f ( x n ) f(x_{n+1})-f(x_n) f(xn+1)−f(xn)为差分,则数值导数是 f ( x ) f(x) f(x)的差分与 x x x的差分的商,所以也叫差商。
仍以 sin x \sin x sinx为例,假设在 [ − 5 , 5 ] [-5,5] [−5,5]区间内分别以0.1,0.5,1为间隔,算其差商,然后和其导数 cos x \cos x cosx相对比。
x = seq(-5,5,0.1)
y = cos(x)
x1 = seq(-5,5,0.1)
end = length(x1)
y1 = (sin(x1[2:end])-sin(x1[1:end-1]))/0.1
x5 = seq(-5,5,0.5)
end = length(x5)
y5 = (sin(x5[2:end])-sin(x5[1:end-1]))/0.5
x10 = seq(-5,5,1)
end = length(x10)
y10 = (sin(x10[2:end])-sin(x10[1:end-1]))/0.5
plot(x,y,type="l",col="red")
lines(x1[2:length(x1)],y1)
lines(x5[2:length(x5)],y5)
lines(x10[2:length(x10)],y10)
如图所示
由于我们采用的是后向差分,所以三组差商的值整体右移。此外,随着 h h h的增大,其误差也越来越明显。
对一个函数进行反复求导,即可得到高阶导数,可以用数学归纳法的方式记为
f ( n ) ( x ) = { f ( n − 1 ) ( x ) } ′ f ( 1 ) ( x ) = f ′ ( x ) \begin{aligned} f^{(n)}(x)&=\{f^{(n-1)}(x)\}'\\ f^{(1)}(x)&=f'(x) \end{aligned} f(n)(x)f(1)(x)={f(n−1)(x)}′=f′(x)
差商亦然,可以记为
f ( n ) [ x ] = { f ( n − 1 ) [ x ] } ′ f ( 1 ) [ x ] = f [ x ] \begin{aligned} f^{(n)}[x]&=\{f^{(n-1)}[x]\}'\\ f^{(1)}[x]&=f[x] \end{aligned} f(n)[x]f(1)[x]={f(n−1)[x]}′=f[x]
但与导数不同之处在于,差商可以更加方便地进行递推,例如
f ( 2 ) [ x ] = f [ x + h ] − f [ x ] h = f [ x + 2 h ] − f [ x + h ] h − f [ x + h ] − f [ x ] h h = f [ x + 2 h ] − 2 f [ x + h ] + f [ x ] h 2 \begin{aligned} f^{(2)}[x]&=\frac{f[x+h]-f[x]}{h}\\ &=\frac{\frac{f[x+2h]-f[x+h]}{h}-\frac{f[x+h]-f[x]}{h}}{h}\\ &=\frac{f[x+2h]-2f[x+h]+f[x]}{h^2} \end{aligned} f(2)[x]=hf[x+h]−f[x]=hhf[x+2h]−f[x+h]−hf[x+h]−f[x]=h2f[x+2h]−2f[x+h]+f[x]