OpenCV图像处理实操

一、空域图像处理

1.1 灰度变换

1.1.1 灰度图像二值化

import cv2

#使用cv2中的thredshold函数
img_input = cv2.imread('.\images\cameraman.tif', cv2.IMREAD_GRAYSCALE)
cv2.imshow('input',img_input)
ret, im_binary = cv2.threshold(img_input, 80, 255, cv2.THRESH_BINARY) #ret表示是否二值化成功的真值,im_binary是二值化图像
if ret:
    cv2.imshow('output',im_binary)
cv2.waitKey(0)
cv2.destroyAllWindows()

#方法二,直接修改原图像
img_input = cv2.imread(r'.\images\cameraman.tif', cv2.IMREAD_GRAYSCALE)
cv2.imshow('input',img_input)
threshold = 80
img_input[img_input > threshold] = 255 # 二值化,超过阈值的像素置白
img_input[img_input <= threshold] = 0 # 二值化,没超过阈值的像素置黑
cv2.imshow('output',img_input)
cv2.waitKey(0)
cv2.destroyAllWindows()

若设阈值为20，输出图像如下：

若设阈值为150，输出图像如下：

显然，阈值设定越低，输入图像中的多数像素都能超过阈值，从而被置为白像素，所以阈值为20的输出图像的白色偏多。反过来，阈值设定过高，输入图像的多数像素无法超过阈值，被置为黑像素，从而黑色变多

1.1.2 图像反转

import cv2

img = cv2.imread('.\images\cameraman_256.tif')
reverse = 256-1-img 
#反转公式s=L-1-r,L-1是灰度级范围,r是原像素,s是输出像素

cv2.imshow('input',img)
cv2.imshow('output',reverse)
cv2.waitKey(0)
cv2.destroyAllWindows()

1.1.2 对数变换

import cv2,numpy as np

img_input = cv2.imread(r'.\images\pollens.tif')
img_output = 42*np.log(1.0+ img_input) 
#s=clog(1+r),r、s分别是输入像素和输出像素
img_output = np.uint8(img_output +0.5) #
对数运算结果转为8位无符号整型

cv2.imshow('input',img_input)
cv2.imshow('output',img_output)
cv2.waitKey(0)
cv2.destroyAllWindows

尝试不同的尺度比例常数 c 值 ， 比较所得图像如下
令c值为10，输出图像：

令c值为80，输出图像：

当c=10，对数运算对低灰度值的拉伸不明显，同时还压缩了高灰度值，所以图像表现为对比度降低，整体呈暗(低灰度值偏多)。当c=80，对数运算明显拉高了低灰度值，同时也稍微压缩了高灰度值，但是因为系数较高，压缩不明显，因此表现为图像对比度较大，原图像的暗处变亮了许多。

1.2图像运算

1.2.1 图像加法

import cv2,numpy as np

img = cv2.imread('.\images\cameraman_256.tif')
img2 = cv2.imread('.\images\lena_color_256.tif')
output_img = cv2.add(img,img2) #图像相加

cv2.imshow('input1',img)
cv2.imshow('input2',img2)
cv2.imshow('output',output_img)
cv2.waitKey(0)
cv2.destroyAllWindows

叠加后图像整体偏亮，因为两图像的像素灰度值加在一起后，像素灰度值肯定是增大的。

1.2.2 图像减法

import cv2,numpy as np

img1 = cv2.imread('.\images\cameraman_256.tif')
img2 = cv2.imread('.\images\lena_color_256.tif')
output_img1 = cv2.subtract(img1,img2) #灰度图减彩色图
output_img2 = cv2.subtract(img2,img1) #彩色图减灰度图

cv2.imshow('input1',img1)
cv2.imshow('input2',img2)
cv2.imshow('output1',output_img1)
cv2.imshow('output2',output_img2)
cv2.waitKey(0)
cv2.destroyAllWindows

灰度图减彩色图的输出结果是output1(从左往右第三张图),彩色图减灰度图的结果是最右边的output2。由于图像相减，出现负值需要取0，因此由灰度图减彩色图的output1中的大多数像素灰度都会出现负值并置为0，导致输出图像整体呈暗色；而由彩色图减灰度图的output2中的大多数像素灰度都是大数减小数，故灰度值降低，导致输出图像是原彩图整体变暗(其中摄影师大衣可以认为灰度值为0，减去大衣等于没减，所以从第四张图中可以发现，大衣那部分其实就是原彩图的部分，被大衣框了起来)

1.2.3 图像融合

import cv2,numpy as np

img = cv2.imread('.\images\cameraman_256.tif')
img2 = cv2.imread('.\images\lena_color_256.tif')
output_img = cv2.addWeighted(img,0.6,img2,0.4,0) 
#st=addWeighted(img,alpha,img2,beta,gamma)
#=img*alpha + img2*beta + gamma

cv2.imshow('input1',img)
cv2.imshow('input2',img2)
cv2.imshow('output',output_img)
cv2.waitKey(0)
cv2.destroyAllWindows

令alpha=0.2，beta=0.8，输出图像如下：

结合对比上面的alpha=0.4，beta=0.6所输出图像，可见alpha和beta分别是第一幅图和第二幅图的融合权重，权重越大，在融合图像中越显清晰。

在上面的alpha=0.4，beta=0.6的基础上，令gamma=100和-100,分别得到输出图像如下:（左gamma=100，右gamma=-100）


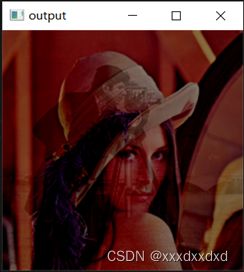
可见，gamma起到了调节亮度的作用。取值越大，融合图像越亮

1.3 直方图修正

1.3.1 直方图均衡化

import cv2

img = cv2.imread(r'.\images\cameraman.tif', cv2.IMREAD_GRAYSCALE)
 #读取灰度图
equ = cv2.equalizeHist(img) #直方图均衡化

cv2.imshow('input',img)
cv2.imshow('output',equ)
cv2.waitKey(0)
cv2.destroyAllWindows

结果分析：直方图均衡化是将原图像的灰度概率密度分布变换得更均匀，所以输出图像有些地方变亮(天空、大衣较明显)，有些地方变暗(建筑底下、草地)

1.4 空域滤波

1.4.1图像平滑（均值滤波、中值滤波、高斯滤波）

import cv2
img = cv2.imread('.\\images\\lena_color_512_saltpepper.jpg ') # 读取图片
result_blur = cv2.blur(img, (3, 3)) #均值滤波
result_GaussianBlur = cv2.GaussianBlur(img, (3, 3), 0) # 高斯滤波
result_medianBlur = cv2.medianBlur(img, 3) # 中值滤波
cv2.imshow('original', img)
cv2.imshow('result_blur', result_blur)
cv2.imshow('result_GaussianBlur', result_GaussianBlur)
cv2.imshow('result_medianBlur', result_medianBlur)
cv2.waitKey(0)
cv2.destroyAllWindows()

经对比，中值滤波去噪效果较好。

对每种滤波函数，尝试不同的核大小 ksize ，比较输出的平滑效果：

令ksize=5，结果如下：


令ksize=7，结果如下:


综合对比ksise=3，5，7，可见核越大，滤波后的图像越模糊，平滑效果越差。

1.4.2图像锐化

1）拉普拉斯模板

import cv2
import numpy as np
src = cv2.imread('.\\images\\circuit.tif') #读取图像
#拉普拉斯模板
kernel = np.array([  
    [-1, -1, -1],
    [-1, 8, -1],
[-1, -1, -1]])
#锐化结果图像dst,其中-1表示目标图像和原图像深度一致，kernel 为滤波器模板
dst = cv2.filter2D(src, -1, kernel)
cv2.imshow('original', src)
cv2.imshow('dst', dst)
cv2.imshow('src+dst', src+dst)
cv2.waitKey(0)
cv2.destroyAllWindows()

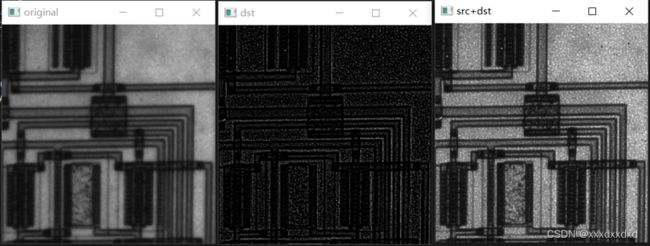
果将上例中滤波模板中心的值由8改为9 ，经filter2D(src, -1, kernel) 滤波后的图像如下：

中心值由8改为9，相当于在原拉普拉斯模板在图像局部进行卷积运算后(假设卷积输出数值为output)，再叠加上原图像局部的中心像素灰度z5：

即在拉普拉斯模板的锐化基础上,叠加了模板中心所对应的原图像素。如上所示，锐化结果更清晰

2）梯度模板(非线性)

import cv2
import numpy as np
src = cv2.imread('.\\images\\circuit.tif')
sobelx = cv2.Sobel(src, cv2.CV_64F, 1, 0) #横向Sobel梯度算子做模板卷积
sobely = cv2.Sobel(src, cv2.CV_64F, 0, 1) #纵向Sobel梯度算子做模板卷积
sobelx = cv2.convertScaleAbs(sobelx) 
#转换为uint8类型(原来是64位浮点型),要转回8位无符号整型才能显示出结果
sobely = cv2.convertScaleAbs(sobely)
sobelxy = cv2.addWeighted(sobelx, 0.5, sobely, 0.5, 0) 
#两个方向的模板卷积结果叠加
cv2.imshow("original", src)
cv2.imshow("x", sobelx)
cv2.imshow("y", sobely)
cv2.imshow("xy", sobelxy)
cv2.imshow("original+xy", src+sobelxy)
cv2.waitKey(0)

Original：

x：

y:

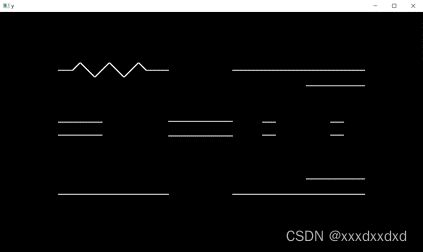
x方向和y方向叠加：

因为垂直(水平)方向的边缘在水平（垂直）方向的梯度幅值较大，所以结果是水平(垂直)方向边缘，两个方向的结果叠加起来就是原图的边缘。

二、图像恢复

2.1 图像去噪

import cv2
img = cv2.imread('.\\images\\lena_color_512_gasuss.jpg ') # 读取图片
result_blur = cv2.blur(img, (3, 3)) #均值滤波,滤波核大小为3×3
result_GaussianBlur = cv2.GaussianBlur(img, (3, 3), 0) # 高斯滤波
result_medianBlur = cv2.medianBlur(img, 3) # 中值滤波
cv2.imshow('original', img)
cv2.imshow('result_blur', result_blur)
cv2.imshow('result_GaussianBlur', result_GaussianBlur)
cv2.imshow('result_medianBlur', result_medianBlur)
cv2.waitKey(0)
cv2.destroyAllWindows()
img_input[img_input > threshold] = 255 # 二值化,超过阈值的像素置白
img_input[img_input <= threshold] = 0 # 二值化,没超过阈值的像素置黑
cv2.imshow('output',img_input)
cv2.waitKey(0)
cv2.destroyAllWindows()

显然，根据结果可以看出，高斯滤波和均值滤波对噪声颗粒较多的区域（如头发、背景紫色部分）滤波效果好，对噪声较密集的区域滤波效果差；中值滤波普遍对各区域的滤波效果较好，对有亮噪声点的区域滤波效果不够好

对每种滤波方法 ，尝试不同的核大小 ksize：
当ksize=5时，效果为：

可见，核越大，去噪效果变得更好，但图像变模糊了

利用上述3种方法对灰度图进行去噪 ：lena_noise.jpg（在文件夹 images），去噪效果的特点如下：


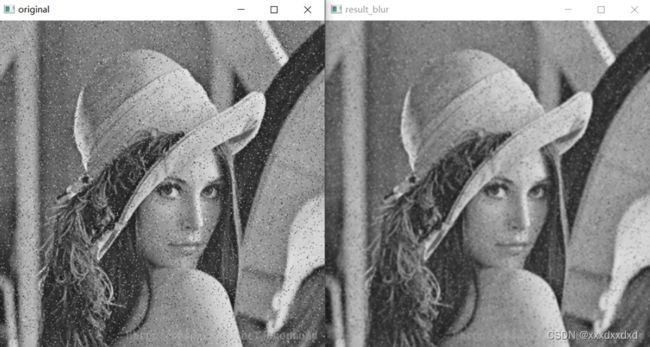
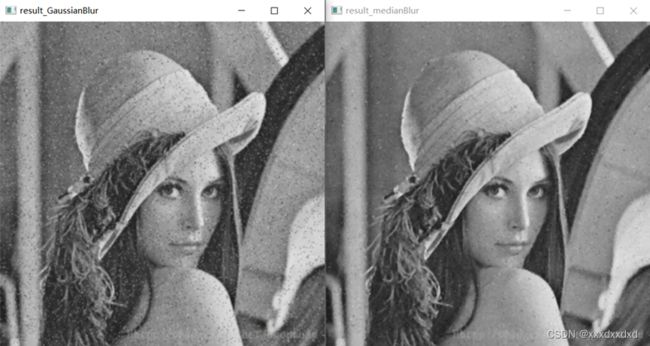
可见，均值滤波和高斯滤波对噪声点都有一定的平滑作用（均值滤波平滑效果稍好，但图像也变得更模糊了）,而中值滤波的滤波效果非常显著，因为针对的是椒盐噪声，取中值显然可以掩盖黑白两个极端点，所以效果是最好的

2.2 图像修补

1.	尝试修补文件夹 images 里的以下图像 ：lena_inpaint 、lena_inpaint3、lena_inpaint6 、lena_inpaint7 
import cv2
img_origin = cv2.imread("./images/lena.bmp ")
img_inpaint = cv2.imread('./images/lena_inpaint.bmp ') # 读取图片
img_origin_gray = cv2.cvtColor(img_origin, cv2.COLOR_BGR2GRAY)
img_inpaint_gray = cv2.cvtColor(img_inpaint, cv2.COLOR_BGR2GRAY)
mask = img_origin_gray - img_inpaint_gray
# 把 mask 变为二值化的 mask_binary，因为后面 cv2.inpaint()的第二个参数必须是二值图像（白色表示要修补的地方）
threshold = 20
ret, mask_binary = cv2.threshold(mask, threshold, 255, cv2.THRESH_BINARY)
# 调用 cv2.inpaint()进行图像修补
dst_TELEA = cv2.inpaint(img_inpaint, mask_binary, 15, cv2.INPAINT_TELEA)
dst_NS = cv2.inpaint(img_inpaint, mask_binary, 15, cv2.INPAINT_NS)
# 显示图像
cv2.imshow("inpaint image ", img_inpaint)
cv2.imshow("result image of TELEA ", dst_TELEA)
# 等待显示
cv2.waitKey(0)
cv2.destroyAllWindows()

lena_inpaint:

lena_inpaint3:

lena_inpaint6:

lena_inpaint7:

对上述各图像的修补情况，描述以下因素对修补效果的影响：
1)被抹掉区域的尺度大小、纹理多少（丰富程度）；
答：被抹掉区域的尺度越大、纹理越丰富，修补效果越差，像是打了马赛克一样。
2)inpaint() 的第 3 个参数 inpaintRadius 取不同的值。
答：以lena_inpaint3和lena_inpaint6为例对比NS算法和TELEA算法：


可见，当第三个参数取NS算法的图像恢复结果的色彩过渡不比TELEA算法连续自然，褶皱感较明显

另外找一幅图像 ，并抹掉不同尺度、位置的区域后进行修补，观察修补的效果
输入待修补图像1（小尺度）：

输出修补图像：

输入待修补图像2（大尺度）：

输出修补图像：

综合对比以上结果，可见待修补区域尺度越小、图像恢复结果越好，色彩过渡越自然。

#三、图像分割

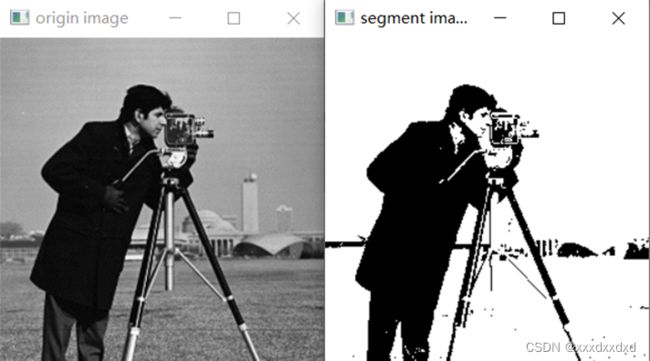
3.1 基于单阀值的图像分割

import cv2
from matplotlib import pyplot as plt
img = cv2.imread(r'.\images\pollens_512.tif', cv2.IMREAD_GRAYSCALE)
#img = cv2.imread(r'.\images\lena_gray_256.tif', cv2.IMREAD_GRAYSCALE)
plt.hist(img.ravel(), 256, [0,256]) # 计算直方图
plt.show()

# 根据直方图选取合适的阀值
threshold = 27
ret, im_segment = cv2.threshold(img, threshold, 255, cv2.THRESH_BINARY)
# 显示图像
cv2.imshow("origin image ", img)
cv2.imshow("segment image", im_segment)
# 等待显示
cv2.waitKey(0)
cv2.destroyAllWindows()

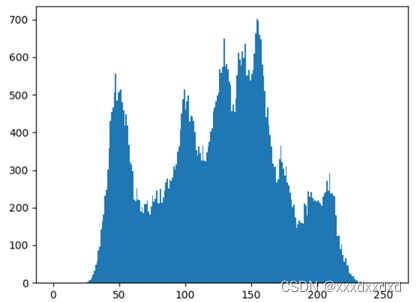
观察并描述程序中两幅图像的直方图（是否呈现一定程度的双峰），并据此找出各自的阀值，然后观察两者基于单阀值的分割效果

程序中两幅图像的直方图，图片Pollens_512的直方图明显呈现双峰，阀值据直方图可以选择25~30之间的数。而lena_gray_256呈现为多峰，可考虑从三处低谷值(75、125、175)中选择，综合比较中间低谷值比较合适

对Pollens_512 选择阀值为27，结果如下:

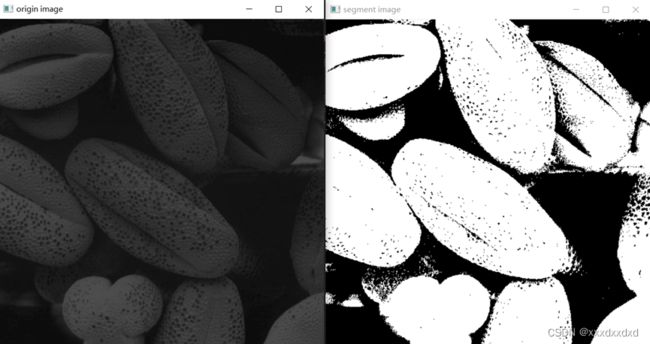
对lena_gray_256选择阀值为125，结果如下:

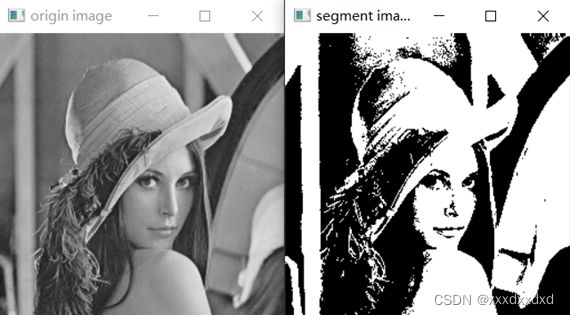
另找一幅单通道图像图像进行单阀值的分割

输入：

灰度直方图如下：

选择阀值为50~100之间的数，考虑阀值为75。输出如下结果：

4.2 基于自适应阀值的图像分割

import cv2
from matplotlib import pyplot as plt
img = cv2.imread(r'.\images\pollens_512.tif', cv2.IMREAD_GRAYSCALE)
plt.hist(img.ravel(), 256, [0,256]) # 计算直方图
plt.show()
# 根据直方图选取合适的阀值
blocksize = 13 #设定区域大小
C = 2 #C = 阈值-领域内均值
im_segment = cv2.adaptiveThreshold(img, 127, cv2.ADAPTIVE_THRESH_GAUSSIAN_C, cv2.THRESH_BINARY, blocksize, C)
# 显示图像
cv2.imshow("origin image ", img)
cv2.imshow("segment image", im_segment)
# 等待显示
cv2.waitKey(0)
cv2.destroyAllWindows()

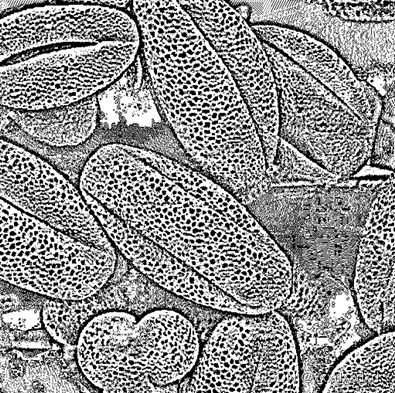
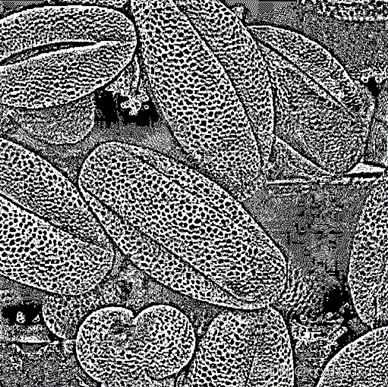
在单阀值分割的程序基础上，改为调用cv2.adaptiveThreshold来运行实验，观察函数 adaptiveThreshold 的最后两个参数 Block Size、C 取不同值时，对分割效果有什么影响
在上面的代码中， C不变，修改blocksize为5、17，得到结果如下：


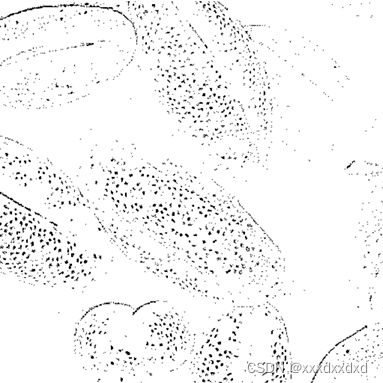
在上面的代码中， blocksize不变，修改C为0、10，得到结果如下：


另找一幅单通道图像进行自适应阀值的分割

输入图像：

设定Blocksize=11、C = 10,输出结果如下：

自适应阀值算法的核心在于以blocksize为大小将图像分成一块一块的区域，然后对每个区域都计算阈值（=该区域内所有像素的均值+C），对于复杂的图像，自适应阀值比单阀值更好处理。