带权并查集
不同于普通的并查集,带权并查集是在并查集的基础上,根据题目的含义,对每一个节点赋予权值含义,在并查集的合并操作中,同时对权值进行操作。
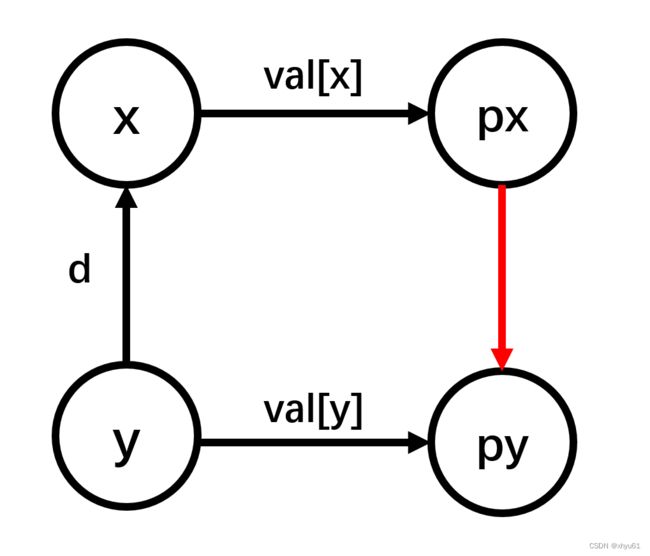
不难看出,合并时 y y y的父节点 p y py py的变化为:
fa[py] = px;
val[py] = -val[y] + d + val[x];
合并时的代码:
void merge(int x, int y, int v) {
int px = find(x), py = find(y);
if (px != py) {
fa[px] = py;
val[px] = -val[x] + v + val[y];
}
}
查询祖先时,对于节点 x x x,设其当前的父节点 t t t,那么val[x]就是从 x x x到 t t t这段。更新了父节点后父节点变成了 p p p,然后当前的val[t]就是 t t t到 p p p这一段。根据路径压缩,我们的节点 x x x最终也要只想 p p p,那么其权值就是从 x x x到 t t t这段的val[x]增加一段 t t t到 p p p这一段的距离(现在是val[t])。
int find(int x) {
if (x == fa[x]) return x;
int t = fa[x];
fa[x] = find(fa[x]);
val[x] += val[t];
return fa[x];
}
NOI 2001 - 食物链
题目链接
解法
题目关键是 A A A吃 B B B, B B B吃 C C C, C C C吃 A A A。这是一个循环的食物链。如果我们给每一个动物编号,那么其实相当于可以根据编号给这些动物划分成三个等价类,分别归类到 A , B , C A,B,C A,B,C中去。不难发现,这个等价类是一个 m o d 3 \bmod 3 mod3等价类。 也就是说,如果两个动物的编号对 3 3 3取模后相等,那么这两个动物是同一类动物;如果两个动物的编号对 3 3 3取模后差值为 1 1 1,则其中存在捕食关系。
换言之,我们给每一个动物赋予的权值,就是这个编号。节点与节点的关系,就靠捕食关系来完成。
我们设编号在模 3 3 3意义下, 1 1 1可以吃 0 0 0, 0 0 0可以吃 2 2 2, 2 2 2可以吃 1 1 1。
对于给定的 x , y x,y x,y:
如果他们都已经在同一个食物网中,那么判断他们是不是同类,只需要看他们是不是模 3 3 3等价类。判断他们是否有捕食关系,只需要看他们的权值之差在模 3 3 3意义下是不是 1 1 1(注意捕食先后顺序)。
如果他们中仅有一个不在食物网中,或他们不在同一个食物网中,则将在食物网中的那个节点设为不在食物网中的那个节点的父亲,然后将后者并入前者的并查集。
如果他们都不在食物网中,任选一个作为父亲,建立一个新的并查集。
Code:
#includePOJ 2492 - A Bug’s Life
题目链接
和食物链题目几乎一样,只不过两种性别将虫子变成模 2 2 2等价类。同性别虫子的编号模 2 2 2意义下相同(要么是 0 0 0,要么是 1 1 1)。
(cin cout不关同步会t,每组数据后面不多输出一个空行会格式错误。)
Code:
#include