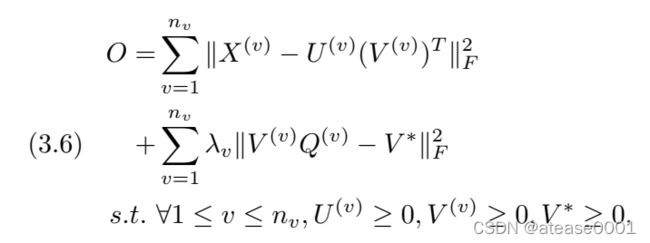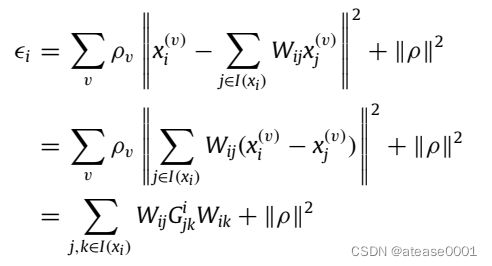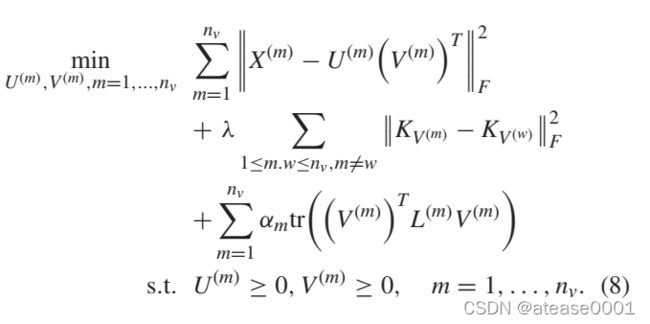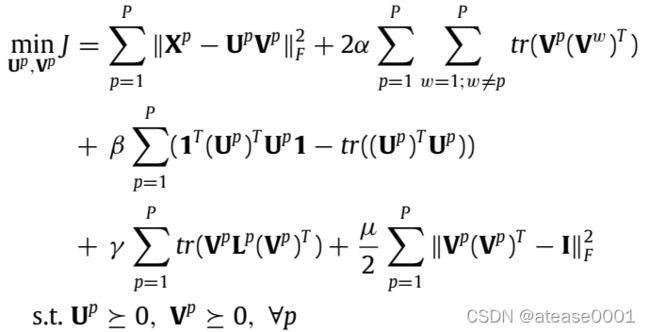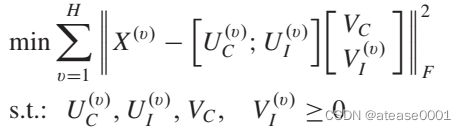基于非负矩阵分解多视图聚类

一般这类方法的目标函数主要分为三部分：（1）各个试图的矩阵分解，得到各个试图的新的表示。（2）融合多个视图的数据得到一致的表示；（3）对表示进行正则；

主要文章：

1.Multi-View Clustering via Joint Nonnegative Matrix Factorization   icdm 2013

这篇文章是目前能查得到的第一篇关于这一模型的文章。其目标函数为：

第一部分为 U为基矩阵（类似空间中的基向量），V为系数矩阵。第一部分为各个试图数据的非负矩阵分解的。

第二部分为多视图融合环节

2.Feature extraction via multi-view non-negative matrix factorization with local graph regularization  icip 2015

在方法1的基础上加上了 graph 正则，目标函数如下：

3.Multi-view Clustering via Multi-manifold Regularized Nonnegative Matrix Factorization. icdm 2014

Multi-view clustering via multi-manifold regularized non-negative matrix factorization.  Neural Networks ,2017

两篇文章是同一作者写的。这篇文章讨论了两个方面（1）得到的最终的表示的形式（2）多视图数据的邻接图的构造方法

最终的表示的两种形式：（a）与方法1一致。目标是得到一个最终的V；（b）最终的表示为每个视图表示线性组合，

(2)图的构造：（a）线性组合 ,

(b)利用LLE算法进行构造：

 两两组合衍生出4种算法。

4.Multiview Clustering Based on Non-Negative Matrix Factorization and Pairwise Measurements。 IEEE Transactions on Cybernetics 2019

这篇文章探讨了，怎样来融合多个视图的表示，进而得到最终的表示：

（1）最小化各个视图表示的V_i和V_j的二范数

 （2）最小化各个视图表示的核的K_i= V_i'V_i和K_j = V_j'V_j的二范数

最终的目标函数为：

（a）

 (b) 

5. Deep graph regularized non-negative matrix factorization for multi-view clustering. Neurocomputing 2020

该方法利用多层矩阵分解得到不同视图的表示，最小化各个视图的表示与最终表示的二范数，然后加上图正则。目标函数如下：

6.Diverse Non-Negative Matrix Factorization for Multiview Data Representation. IEEE TRANSACTIONS ON CYBERNETICS, VOL. 48, NO. 9, SEPTEMBER 2018

这篇文章的作者认为不同的试图的数据中含有的不同的信息有利于聚类任务，同时最终的表示应该为各个视图的最终表示的线性组合。因此，这篇文章加入了各个视图的差异化的度量为：

 最终的目标函数为：

7.Multi-view clustering by non-negative matrix factorization with co-orthogonal constraints。  Knowledge-Based Systems 2020
 

这篇论文为文献6的改进版本，加入了

（1）基矩阵的正交限制；这个很容易理解，是降低表示在不同维度之间的信息冗余

（2）表示的正交限制；与（1）相似。为了降低不同维度的数据的之间的相似性，以增加信息

 8.Co-Learning Non-Negative Correlated and Uncorrelated Features for Multi-View Data. 2021 TNN 

这种算法与文章6-8类似，认为多视图数据中蕴含互补信息。为了利用这种信息，矩阵分解部分变化为：

在上式基础上加上流形正则，以及稀疏限制。目标函数定义为：

与其他方法不同的是，最终的表示为Vc, 以及各个视图V_i串联形式。

10.Multi-View Clustering via Deep Matrix Factorization  AAA 2017

采用深度Semi-NMF计算各个视图的表示V_i，图正则。目标函数如下：

11. Auto-weighted multi-view clustering via deep matrix decomposition。 2020 Pattern Recognition

与前几种算法不同，该算法设置V_r是离散的。在优化过程，与其他方法不同

12.Multi-view Clustering via Deep Matrix Factorization and Partition Alignment。2021 MM

该算法目标函数可分为两部分（1）利用semi_nmf计算各个视图的表示H_m，(2)融合各个视图的表示以得到最终的表示：

总结，基于多视图矩阵分解的聚类目前的主要的创新点可分为三点：

（1）改进各个视图的矩阵分解部分

        （a）修改范数得到更鲁棒的表示；（文献11，Lp，L2,p范数等）

        （b）利用深度矩阵分解代替传统的非负矩阵分解；（文献10-12）

        （c）限制基矩阵（文献7）

（2）利用图正则方法来正则得到的表示，邻接图的计算方法（自适应，或者其他形式）

（3）融合多个视图的数据

        （a）目标为得到一致的表示，探索不同的融合策略（即文献4和12）；

        （b）目标为各个视角的线性组合；

原创不易，谢绝转载！！！