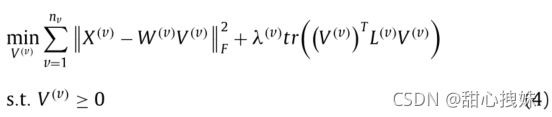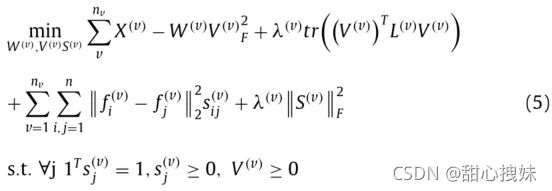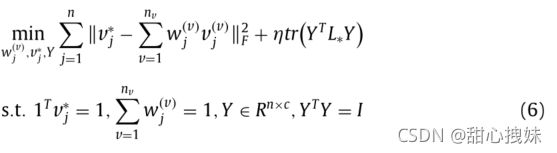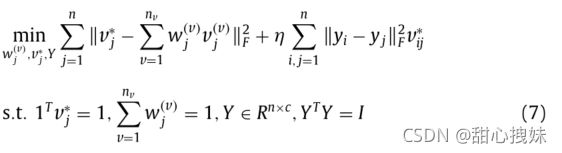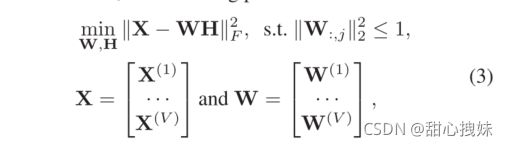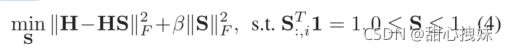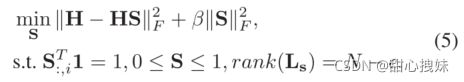多视图聚类（矩阵分解篇）

1.《基于稀疏表示和自适应加权合作学习》

paper:Multi-view subspace clustering with intactness-aware similarity

(Junpeng Tan a , Zhijing Yang a , ∗, Yongqiang Cheng b , Jielin Ye a , Bing Wang b , Qingyun Dai c )2021

 引言：

非负矩阵存在局限：丢弃一些有用的negative信息。

CL动机：对每个视图进行协作训练，以获得包含每个视图的多样性信息的全局矩阵，可以充分利用视图之间的多样性信息，还有实现视图之间的互补性。

现存方法问题：1.在原始数据的SR中，NMF需要非负输入数据和基矩阵上的非负约束，这导致在分解过程中过滤掉负输入数据中包含的一些有用信息；2.它缺乏提取视图特定信息的有效方法。现有的方法很难获得最优的内部结构特征，因为数据往往包含一些冗余噪声；3.独立使用SR、自适应图学习（AGL）或CL不能充分考虑视图的多样性和视图之间的全局性。

本文贡献：1.提出了一种独特的稀疏矩阵分解方法，放松了NMF基矩阵的非负约束，使矩阵分解得到的稀疏矩阵包含更多有用信息；2.采用直接导数法对基矩阵和稀疏矩阵进行有效优化。因此，它增加了样本之间的相似性鉴别，同时，对SR的系数矩阵提出了二次处理;3.提出了一种新的两步算法来同时解决视图特定信息的学习和融合问题。首先，我们应用AGL优化相似矩阵，并通过组合流形学习对每个视图的内部结构特征进行预处理。AGL和SR的集成可以提取每个视图的特定信息。在此基础上，提出了一种AWCL融合方法来有效融合视图的分集信息。通过自适应加权方法学习全局矩阵进行融合，获得不同视图的特定信息。为了形成完整的全局矩阵数据结构，对全局矩阵进一步应用流形学习。

 方法

第一项是稀疏的模型表示，可以移除多余的信息，第二项是流形表示，保存内部结构信息

 连续优化过程获得最佳稀疏矩阵和最优相似度矩阵

 其中，fi(v)是拉普拉斯矩阵L（v）的第i个特征向量，第三和第四项是相似度矩阵的自适应学习

 自适应加权协作学习

其中，Y'是拉普拉斯矩阵Lstar为了全局矩阵）的特征向量矩阵 ,加入矩阵正则化约束：

算法： 

  

---

 2.《潜在嵌入空间》

解决问题：1.以前方法通常依赖于每个视图中的原始特征，但仍然缺乏发现多视图数据的统一表征表示的能力。2.在谱聚类阶段，它们大多倾向于考虑谱聚类的两个分量。（即，亲和矩阵构造和聚类指标矩阵计算）分别进行，但通常缺乏在优化框架中同时表述这两个组件的能力。

针对上述局限性，本文提出了一种统一的潜在嵌入空间多视图聚类框架（MCLES）。该方法在统一的模型中联合学习潜在嵌入表示、相似信息和聚类指标矩阵。从多视图特征中学习到的潜在嵌入空间能够探索这些关系在不同的样本之间，避免可能的损坏以及维度限制。利用自表达的思想，基于学习到的潜在嵌入表示而非数据的原始特征构造相似矩阵。此外，聚类指标矩阵直接学习，无需额外的谱聚类过程。

全局相似度学习

与LLE相似，根据自表达特性，每个数据点都可以由其他数据点的线性组合表示：

其中，S是相似度矩阵（权重） 

方法

启发：假设多个视图来自一个潜在表示，该潜在表示从本质上描述了数据，并发现了不同视图之间共享的潜在结构，我们的方法旨在为每个数据点发现一个共享的潜在嵌入表示hi，这样所有这些不同的视图都是从潜在嵌入空间H中提取的。

求解以下问题得到H：

其中W是映射模型， 在W上的约束是为了避免H在缩放时过小。

与以往方法从原始数据中学习相似度矩阵相比，该方法从潜在嵌入空间学习相似矩阵，有效提高了学习相似矩阵的鲁棒性和准确性，根据全局亲和性学习：

 理想情况下，S是一个准确的具有c个连通特性的块对角矩阵。然而4的求解可能并不尽如人意，因此我们需要加入秩约束：

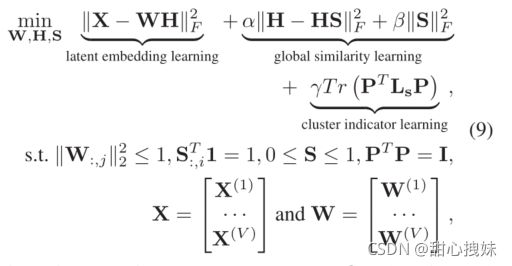
整体目标函数：

为了便于求解，将秩约束变成正则化因子放入函数中：

最终： 

 实验

数据集：MSRCv1：210样本,7类，4个视图

结果：0.8810   0.7943  0.8810