GPU/DCU减少cudaMemcpy/hipMemcpy时间方案
前言
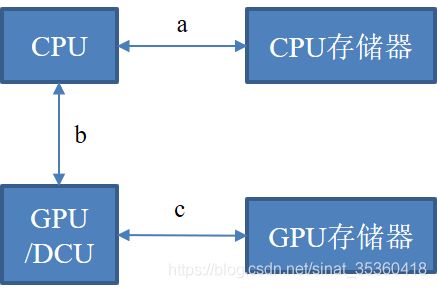
CUDA是GPU加速器上的编程语言,HIP是DCU加速器上的编程语言,二者生态相似,CUDA可通过hipify工具转换为HIP HIP docs: https://rocmdocs.amd.com/en/latest/index.html如上图所示,cudaMemcpy/hipMemcpy的时间应该由三部分组成,分别是CPU的访存时间、CPU到加速卡的时间、还有加速卡的访存时间。
| 曙光超算节点 | 天河2A超算节点 | |
|---|---|---|
| a带宽 | DRMA:30~40GB/s | DRMA:30~40GB/s |
| b带宽 | PCIe 3.0 x16: 16GB/s | PCIe 3.0 x16: 16GB/s |
| c带宽 | HBM2: 1TB/s | GDDR5: 480GB/s |
| 加速卡计算峰值 | DCU: 5.7Tflop/s | GPU:2.91 Tflop/s |
上表对比了曙光先进计算服务平台节点和天河2A超算节点的带宽与加速卡峰值,可以看到两台超算的a、b、c三者中b是主要的瓶颈,也就是CPU到加速卡的时间,主要受限于PCIe总线带宽。PCIe 3.0 x16的带宽和计算峰值几个Tflop/s相差太大,所以应该尽量减少主机端和设备之间的数据传输,下文测试了两台超算上的传输时间并探讨减少传输时间的几个方案。
一、传输延迟测试
在两种设备上用了同一个测试用例,测试规模从50万的整型数到2亿个整型数,测试对象主要是从CPU往加速设备端拷贝时间的过程,理论上从主机到设备端和从设备端到主机的时间应该是一致的,循环10次拷贝的过程,每一次都输出,统计时取10次拷贝时间的平均值。然后对同一个节点里的不同加速设备都进行了测试,曙光先进计算服务平台上每个节点里有4个DCU,天河中国国家网格12区上有2个GPU的权限。
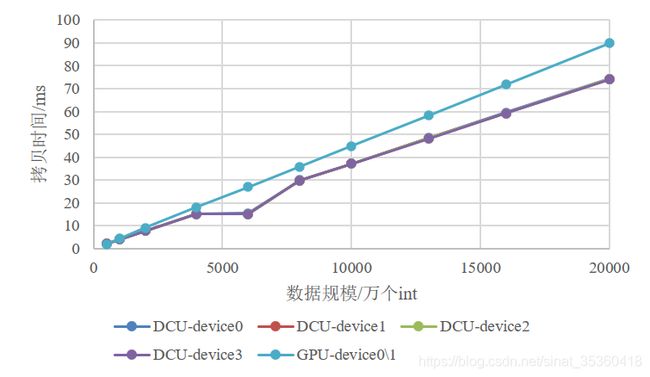
测试结果可以看出较小规模的(也就是1000万整型数、9.5MB以下)的GPU拷贝速度更快,较大规模的DCU拷贝速度更快。
二、减少传输时间方案
1.数据重用
首先应该尽可能地重用数据,能传一次就不传两次。
以Lanczos迭代法为例,该算法的目的是形成矩阵A的三对角矩阵T:
T = [ α 1 β 1 0 β 1 α 2 ⋱ ⋱ ⋱ ⋱ ⋱ α n − 1 β n − 1 0 β n − 1 α n ] T=\left[\begin{array}{lllll}\alpha_{1} & \beta_{1} & & & 0 \\ \beta_{1} & \alpha_{2} & \ddots & & \\ & \ddots & \ddots & \ddots & \\ & & \ddots & \alpha_{n-1} & \beta_{n-1} \\ 0 & & & \beta_{n-1} & \alpha_{n}\end{array}\right] T=⎣⎢⎢⎢⎢⎡α1β10β1α2⋱⋱⋱⋱⋱αn−1βn−10βn−1αn⎦⎥⎥⎥⎥⎤
T = Q T A Q T=Q^{T}AQ T=QTAQ, Q = [ q 1 , q 2 , . . . , q n ] Q=[q_{1},q_{2},...,q_{n}] Q=[q1,q2,...,qn],Q是正交矩阵, q i q_{i} qi是Q的列向量,其迭代格式为:
- α 1 = q 1 T A q 1 \alpha_{1}=q_{1}^{T} A q_{1} α1=q1TAq1
- r i = A q i − α i q i − β i − 1 q i − 1 r_{i}=A q_{i}-\alpha_{i} q_{i}-\beta_{i-1} q_{i-1} ri=Aqi−αiqi−βi−1qi−1
- β i = ∣ r i ∣ 2 \beta_{i}=\left|r_{i}\right|_{2} βi=∣ri∣2
- q i + 1 = r i / β 1 q_{i+1}=r_{i} / \beta_{1} qi+1=ri/β1
- α i + 1 = q i + 1 T A q i + 1 , i = 1 , 2 , ⋯ , k \alpha_{i+1}=q_{i+1}^{T} A q_{i+1}, i=1,2, \cdots, \mathrm{k} αi+1=qi+1TAqi+1,i=1,2,⋯,k
每一次迭代的过程都会求得矩阵Q的一个列向量 q i q_{i} qi,但本次迭代是依赖于上一次迭代求得的列向量 q i − 1 q_{i-1} qi−1的,所以算法整体有很强的数据相关性,难以对整个迭代过程并行化,但是可以对Lanczos过程中的计算热点稀疏矩阵向量乘 A q i A q_{i} Aqi进行并行化。
并行思路是将A矩阵按行划分,使用GPU/DCU等加速卡,把N行分到N个线程块中去计算。可以看到迭代过程虽然是数据相关的,但只要用到上一次迭代的 q i − 1 q_{i-1} qi−1向量,而规模最大的A矩阵在每一次迭代中都是一样的,所以可以只在迭代的第一次把A传到设备端,使用__device__标识的全局变量把它存起来,后面的迭代直接从全局变量中取,可以省不少时间。
2.Pinned Memory
第二个方案是使用锁页内存。所谓锁页内存就是CPU内存中不会被换入换出的一块内存。
主机端内存采用分页式管理,为了提高主机端访存效率,操作系统会经常换入换出DRAM中的页到Cache或外存中,对于主机端程序没有影响,只要逻辑地址正确操作系统会帮助管理物理页。但从主机端传输到设备端过程中为了保证传输的页不被“换走”,需要进行页面锁定,把要传输到GPU的页复制到固定内存,再从固定内存传入到设备内存。这就需要两次传送过程,增加了传输延迟。解决办法是在分配内存的时候,使用cudaMallocHost/hipMallocHost直接从锁页内存里面分配,这样就少了一次传输过程,如下图:
锁页内存是可以自己制定分配多少的,但它的缺点是是分配空间过多可能会降低主机系统的性能,因为它减少了用于存储虚拟内存数据的可分页内存的数量,所以需要在机器上测试合适的锁页内存。
3.高维矩阵传输
第三个方案是使用高维的矩阵传输命令:hipMallocPitch配合上hipMemcpy2D / hipMemcpy3D。通常来讲,在DCU中分配内存使用的是hipMalloc函数,但是对于二维或者三维矩阵而言,使用hipMalloc来分配内存并不能得到最好的性能,原因是对于2D或者3D内存,对齐是一个很重要的性质,而hipMallocPitch或者hipMalloc3D这两个函数能够保证分配的内存是合理对齐的,满足合并访问要求,因此可以确保对行访问时具有最优的效率。
比如说下面这个矩阵a1-a9:
[ a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 ] \left[\begin{array}{lll}a_{1} & a_{2} & a_{3} \\ a_{4} & a_{5} & a_{6} \\ a_{7} & a_{8} & a_{9}\end{array}\right] ⎣⎡a1a4a7a2a5a8a3a6a9⎦⎤
如果用普通的分配方式hipMalloc来存储矩阵,在内存里面他会挨着线性存储,但是用对齐分配方式hipMallocPitch来分配的话,存储的时候他会按照对齐的字节数来存,假如内存是以4个字节对齐的,并且每个线程束里面有4个线程,写入的时候会使每行的首地址对齐,都是4的倍数,即使有没填满的内存也没关系;读取的时候直接三个线程数可以并行读取a1-a9,如下图:
这里只是举一个例子以4个字节对齐,事实上hip访问global memory的过程中,从128字节对齐的地址(addr=0, ,128,256)开始的连续访问是最有效率的。
4.传输、计算时间重叠
第四个方案是将计算和传输时间进行重叠,在hip中可以利用stream流来做到这一点,Stream是一种逻辑队列,如果不指定某指令的stream那它会默认放到0号stream上。假设有3个kernel以及一些内存拷贝函数,launch到默认0号stream上:
![]()
hipMemcpy(d_a1,h_a1,Nbytes,hipMemcpyHostToDevice);
hipMemcpy(d_a2,h_a2,Nbytes,hipMemcpyHostToDevice);
hipMemcpy(d_a3,h_a3,Nbytes,hipMemcpyHostToDevice);
hipLaunchKernelGGL(myKernel1,blocks,threads,0,0,N,d_a1);
hipLaunchKernelGGL(myKernel2,blocks,threads,0,0,N,d_a2);
hipLaunchKernelGGL(myKernel3,blocks,threads,0,0,N,d_a3);
hipMemcpy(h_a1, d_a1, Nbytes,hipMemcpyDeviceToHost);
hipMemcpy(h_a2, d_a2, Nbytes,hipMemcpyDeviceToHostTo);
hipMemcpy(h_a3, d_a3, Nbytes,hipMemcpyDeviceToHost);
也可以通过异步拷贝函数和指定不同stream上的指令流来让计算和拷贝重叠:
hipMemcpyAsync(d_a1,h_a1,Nbytes,hipMemcpyHostToDevice,stream1);
hipMemcpyAsync(d_a2,h_a2,Nbytes,hipMemcpyHostToDevice,stream2);
hipMemcpyAsync(d_a3,h_a3,Nbytes,hipMemcpyHostToDevice,stream3);
hipLaunchKernelGGL(myKernel1,blocks,threads,0,0,N,d_a1);
hipLaunchKernelGGL(myKernel2,blocks,threads,0,0,N,d_a2);
hipLaunchKernelGGL(myKernel3,blocks,threads,0,0,N,d_a3);
hipMemcpyAsync(h_a1, d_a1, Nbytes,hipMemcpyDeviceToHost,stream1);
hipMemcpyAsync(h_a2, d_a2, Nbytes,hipMemcpyDeviceToHost,stream2);
hipMemcpyAsync(h_a3, d_a3, Nbytes,hipMemcpyDeviceToHost,stream3);
5.批量传输、选择大粒度并行
第五个方案是积少成多,把小的数据尽可能合并、打包成为大一点的数据批量传输,因为每次传输过程中不只有传输过程耗时,还有一些其他的开销,比如传输指令本身的延迟。例如下面这个表,实际传输时间和理论传输时间还是有一定差距。
| 数据规模/万个int | 数据规模/MB | DCU实际传输时间/ms | 理论传输时间/ms |
|---|---|---|---|
| 500 | 19.1 | 2.2 | 1.1 |
| 1000 | 38.1 | 4.0 | 2.3 |
| 2000 | 76.3 | 7.8 | 4.7 |
| 4000 | 152.6 | 15.2 | 9.3 |
| 6000 | 228.9 | 15.5 | 14.0 |
还可以提高并行粒度,在数据相关性不高的情况下尽量在循环的外层进行优化,内循环中使用传输函数的开销太大
总结
减少传输时间的方案:
- 数据重用
- 使用pinned memory
- 高维数组使用pitch、2Dcpy方法
- 将数据传输与计算的时间重叠
- 批量传输数据,集小为大
- 避免对小粒度程序并行(e.g 内循环)