数学建模算法与应用【模糊综合评价算法】

了解了模糊数学的相关知识。模糊综合评价算法是用来综合评价与决策的方法。变异系数法可以用来确定权重向量。相对偏差法和相对优属度法可以获取评价矩阵R

相关知识

模糊数学

现实世界中的许多现象和关系具有不确定性。这些不确定性的表现形式多种多样，如随机性.灰色性、模糊性和粗糙性等
模糊数学正是利用模糊集及其运算研究、处理模糊不确定现象和关系的数学分支学科
许多数学建模问题包括模糊现象和关系，这类问题往往可以用模糊数学方法处理。
下面介绍模糊集和模糊综合评价

模糊集

现实中的许多现象及关系比较模糊。如高与矮长与短，大与小，多与少，穷与富
这类现象不满足“非此即彼”的排中律，而具有“亦此亦彼”的模糊性。
模糊不确定不同于随机不确定。随机不确定是因果律破损造成的不确定，而模糊不确定是由于排中律破损造成的不确定


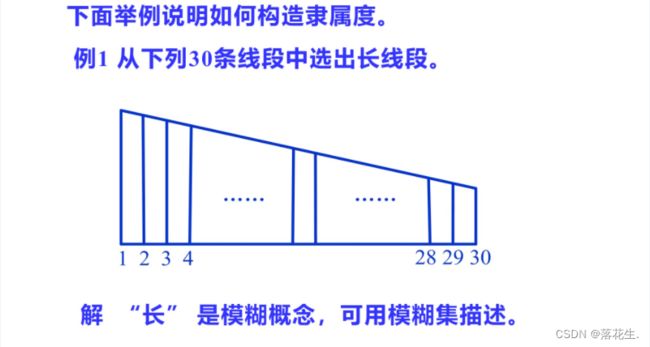
设xi表示第i(i=1,2,…,30)条线段,则论域 U={x1, X2,…, X30}。若A为“长线段”的集合，则线段xi作为集A的成员资格，就是xi对A的隶属度。
下面建立A的一种隶属函数,因为线段越长，属于A 的程度越大所以线段的长短可作为A的隶属度。

模糊集的运算

由于模糊集中没有元素和集合间的绝对隶属关系，所以模糊集的运算是通过隶属函数完成的。

隶属度函数的确定

由模糊集的概念可知，模糊数学的基本思想是隶属度，所以应用模糊数学方法建立数学模型的关键是建立符合实际的隶属函数。然而，如何确定一个模糊集的隶属函数至今还是尚未完全解决的问题
确定隶属度的常用方法是模糊分布法
模糊分布法将隶属函数看成一种模糊分布，首先根据问题性质选取适当的模糊分布，然后再依据相关数据确定分布中的参数
下面简要介绍模糊分布中常用的梯形分布。



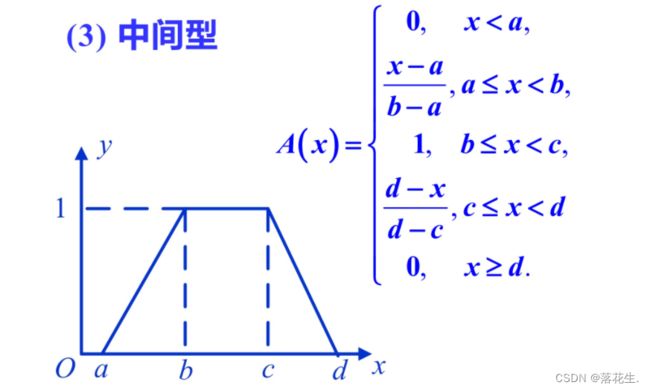
偏小型一般适用于描述“小”“少”"浅"淡”等偏向小的程度的模糊现象;偏大型正好与偏小型相反;而中间型一般适用于描述处于中间状态的模糊现象。

模糊综合评价

对一个事物的评价通常要涉及多个因素或多个指标，评价是在多因素相互作用下的一种综合评判。
综合评价的方法众多，常用的有灰色评价法、层次分析法、模糊综合评价法、数据包络分析法、人工神经网络评价法、理想解法等。有时，还可将两种评价方法集成为组合评价方法
各种评价方法出发点不同，解决问题的思路不同，适用对象不同，各有优缺点
不同的评价方法会产生不同的评价结论，有时甚至结论相左，即综合评价的结果不是唯一的
模糊综合评价作为模糊数学的一种具体应用，基本思想是：以模糊数学为基础，应用模糊关系合成原理，将一些边界不清、不易定量的因素定量化，从多个因素对被评价事物隶属等级状况进行综合评价。
具体步骤为：首先确定被评价对象的因素集和评价集，然后再分别确定各因素的权重及它们的隶属度向量，获得模糊评价矩阵，最后将模糊评价矩阵与因素的权向量进行模糊运算并归一化，从而得到模糊评价综合结果。
模糊综合评价法简单易掌握，对多因素、多层次的复杂问题评价效果较好，很难为其它评价方法所替代。

模糊综合评价步骤

上述综合，基本思想是: 对评价矩阵 R和权向量A进行某种适当的模糊运算，将两者合成为一个模糊向B={b1,b2,…,bn}了即B=A R，然后对B按照一定法则进行综合分析后即可得出最终的模糊综合评价结果。
常用的模糊合成算子有:


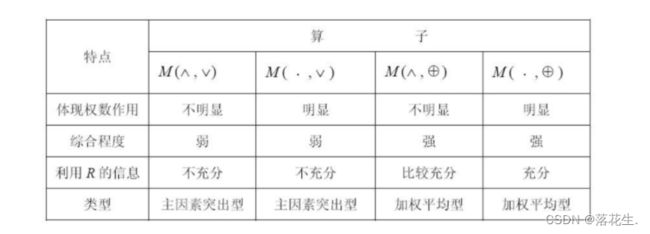
其实，也可以取M为普通的矩阵乘法此时合成即为加权平均。至于到底取何种算子取决于问题的性质和算子的特点。
通常，采用主因素突出型和加权平均型算法的结果大同小异。但在实际中还是要注意这两类算法的特点
主因素突出型适用于模糊矩阵中数据相差很悬殊的情形，而加权平均型则常用于因素很多的情形，可以避免信息丢失。

示例

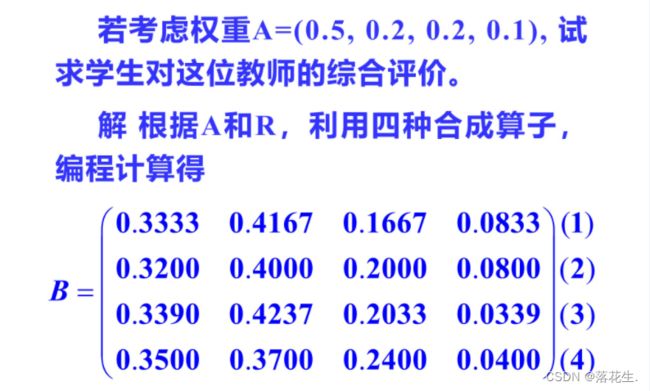
结果表明，学生对该老师在“教材熟悉方面最认可，“清楚易懂”次之，板书整
齐清晰”则得不到认可显然，例3过于简单。不仅给出了模糊综合评价矩阵R，而且还直接给出了权重向量A
其实，实际问题往往只提供了一系列的评价对象以及每个对象的若干评价指标，并且这些指标可能数值差异很大，性质也不同。
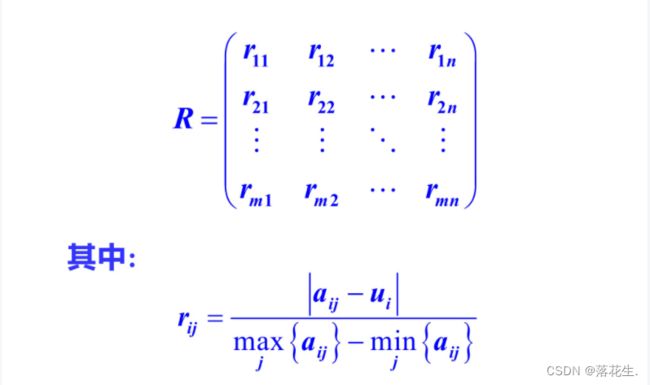
此时，不仅指标的权重向量A需要根据适当的方法确定，就连评价矩阵R也要按照某种方法对评价指标进行处理后才能获得
确定权重向量A的常用方法是前面提到的变异系数法，而处理评价指标获取评价矩阵R的常用方法有相对偏差法和相对优属度法这两种方法简单、实用，在建模竞赛中可考虑与灰色关联分析结合使用。
下面介绍这三种方法

变异系数法

变异系数法的设计原理是: 若某项指标的数值差异较大，能明确区分开各被评价对象，说明该指标的分辨信息丰富，因而应给该指标以较大的权重;反之，若各个被评价对象在某项指标上的数值差异较小，那么这项指标区分各评价对象的能力较弱，因而应给该指标较小的权重。





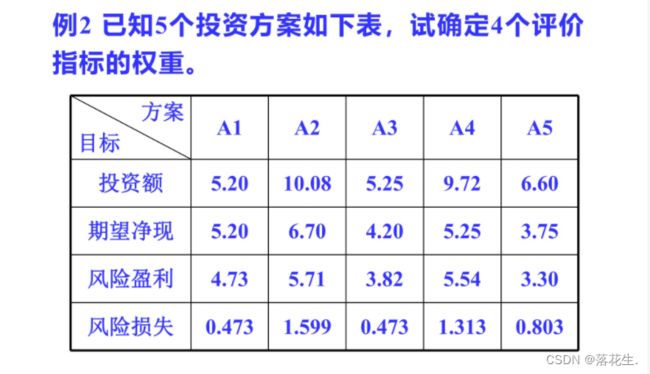
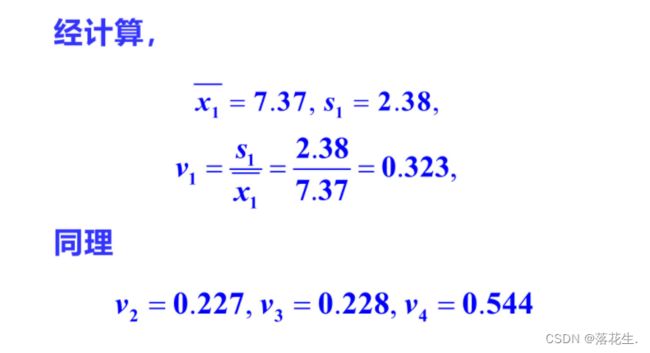
用变异系数法求出的某指标的权重与该指标在评价体系中的重要性是两个概念
变异系数法的作用只是提高指标的分辨能力，利于排序。
其实，使用变异系数法的前提恰恰是所有指标在评价体系中的重要性相当也就是说，当指标在评价体系中的重要性相差较大时，使用变异系数法确定权重并不一定合适

相对偏差模糊矩阵评价法

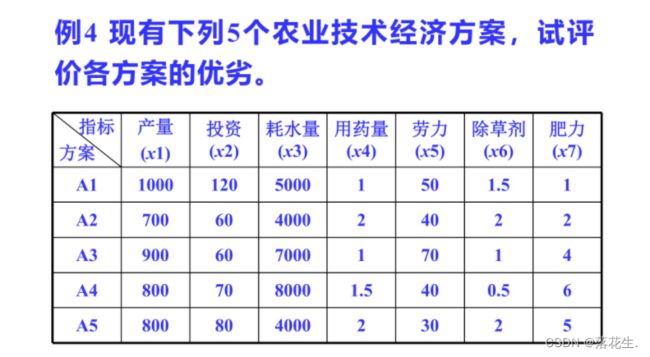
相对偏差模糊矩阵评价法与灰色关联分析有点类似。首先虚拟一个理想方案u，然后按照某种方法建立各方案与u的偏差矩阵R，再确定各评价指标的权重A，最后用A对R加权平均得各方案与权重A，u的综合距离F，则根据F即可对方案进行排序。

代码

A=[1000	120	5000	1	50	1.5	1
700	60	4000	2	40	2	2
900	60	7000	1	70	1	4
800	70	8000	1.5	40	0.5	6
800	80	4000	2	30	2	5];
[m,n]=size(A);%找出多少行多少列
maxA=max(A);%找出每列最大值
minA=min(A);%找出每列最小值
G=maxA-min(A);%最大值减去最小值
A1=max(A(:,1));%A1为效益型
A2=min(A(:,2:n-1));%A2~A6为成本型
A3=max(A(:,7));%A7为效益型
u=[A1,A2,A3];
R=zeros(m,n);%将模糊综合矩阵初值设置为0
% 如下是得出模糊综合矩阵
for i=1:m
    for j=1:n
        R(i,j)=abs(A(i,j)-u(j))/G(j);
    end 
end
%利用变异系数计算权向量
x=mean(A);
s=std(A);%求每一列的方差
v=s./x;%权向量的初值
v2=sum(v);
c=zeros(1,7);
for i=1:7
    c(i)=v(i)/v2;
end

FF=R*c'

运行结果

相对优属度模糊矩阵评价法

相对偏差法的评价依据是各方案与理想方案的偏差，而相对优属度评价法的基本思想是:首先用适当的方法将所有指标(效益型、成本型、固定型)转化为效益型(成本型)，得到优属度矩阵R，再确定各评价指标的权重A最后用A对R加权平均得各方案的综合优属度F，则根据F即可对方案进行排序

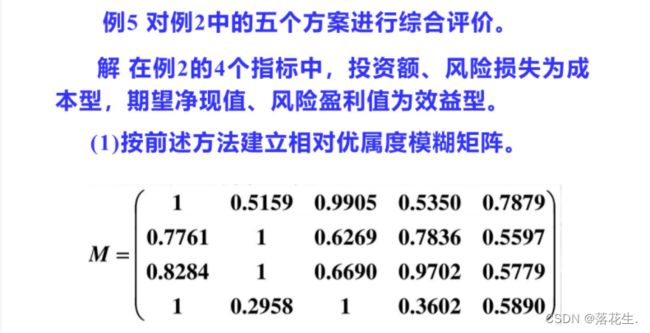
小结

由于灰色关联分析、相对偏差法和相对优属度法均属综合评价类方法,且都有解决同样的问题，所以自然产生一个问题：这三种方法评价同一问题的结论完全一致吗?
首先分别用相对偏差法和相对优属度法评价例5和例4。