单纯形算法 Simplex Algorithm (一)
单纯形算法是求解线性规划问题最经典的方法,在许多介绍该算法的文章中会使用单纯形表(Tableau)辅助计算,而对Tableau进行的操作本质上都是在对松弛化的线性规划模型进行矩阵运算,从几何表现上看,就是在线性规划问题的定义域上的顶点中迭代搜索,寻找使得目标函数最优的那个顶点。使用Tableau计算虽然很高效,不过对于理解算法原理帮助不大;单纯形算法的原理是基于线性代数的,如果要彻底理解,还是需要很多基础的矩阵知识的。这篇文章里我只是记录和单纯形算法相关的线性代数知识,加深对该算法中一些术语的记忆和理解;算法里更加具体的线代原理则跳过,那已经超过了我的认知水平,在后续文章中会记录更容易理解的算法计算过程。
线性规划松弛形式
在应用算法前,必须对原始的线性规划模型进行预处理,先转换成标准线性规划模型,再转换成松弛线性规划模型。标准线性规划模型的形式:
m a x Z = c T x s . t . A x ≤ b x ≥ 0 \begin{aligned} max\quad& Z=\boldsymbol{c}^T\boldsymbol{x}\\ s.t.\quad& \boldsymbol{A}\boldsymbol{x}\leq \boldsymbol{b} \\ & \boldsymbol{x} \geq0 \\ \end{aligned} maxs.t.Z=cTxAx≤bx≥0
具体形式:
m a x Z = c 1 x 1 + c 2 x 2 + . . . + c n x n s . t . [ a 11 a 12 . . . a 1 n a 21 a 22 . . . a 2 n . . . . a m 1 a m 2 . . . a m n ] [ x 1 x 2 . x n ] ≤ [ b 1 b 2 . b m ] x ≥ 0 \begin{aligned} max\quad& Z=c_1x_1+c_2x_2+...+c_nx_n\\ s.t.\quad& \begin{bmatrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ . & . & . & . \\ a_{m1} & a_{m2} & ... & a_{mn} \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ . \\ x_n\\ \end{bmatrix}\leq \begin{bmatrix} b_1 \\ b_2 \\ . \\ b_m\\ \end{bmatrix}\\ & \boldsymbol{x} \geq0 \\ \end{aligned} maxs.t.Z=c1x1+c2x2+...+cnxn⎣⎢⎢⎡a11a21.am1a12a22.am2..........a1na2n.amn⎦⎥⎥⎤⎣⎢⎢⎡x1x2.xn⎦⎥⎥⎤≤⎣⎢⎢⎡b1b2.bm⎦⎥⎥⎤x≥0
如果将一个原始的线性规划模型标准化? 如果目标是最小化,则乘上-1变成最大化目标(当然标准模型的目标函数也可以是最小化,两者本质是相同的,只不过算法的某些细节上互为相反);如果约束是 ≥ \geq ≥,两边同乘-1;如果某个变量 x i < 0 x_i<0 xi<0,那么定义 x i = x ′ − x ′ ′ x_i=x'-x'' xi=x′−x′′,并且 x ′ ≥ 0 , x ′ ′ ≥ 0 x'\geq0,x''\geq0 x′≥0,x′′≥0,将原变量替换成 x ′ x' x′和 x ′ ′ x'' x′′
然后将标准形式转换成松弛形式,其实就是给每个约束不等式上引入松弛变量 s s s,将所有的约束不等式转换成等式:
m a x Z = c T x ′ s . t . A ′ x ′ = b x ′ ≥ 0 \begin{aligned} max\quad& Z=\boldsymbol{c}^T\boldsymbol{x'}\\ s.t.\quad& \boldsymbol{A'}\boldsymbol{x'}= \boldsymbol{b} \\ & \boldsymbol{x'} \geq0 \\ \end{aligned} maxs.t.Z=cTx′A′x′=bx′≥0
即:
m a x Z = c 1 x 1 + c 2 x 2 + . . . + c n x n s . t . a 11 x 1 + a 12 x 2 + . . . + a 1 n x n + s 1 = b 1 a 21 x 1 + a 22 x 2 + . . . + a 2 n x n + s 2 = b 2 . . . a m 1 x 1 + a m 2 x 2 + . . . + a m n x n + s m = b m x 1 , x 2 , . . . , x n , s 1 , . . . , s m ≥ 0 \begin{aligned} max\quad& Z=c_1x_1+c_2x_2+...+c_nx_n\\ s.t.\quad& a_{11}x_{1}+a_{12}x_{2}+...+a_{1n}x_{n}+s_1=b_1 \\ & a_{21}x_{1}+a_{22}x_{2}+...+a_{2n}x_{n}+s_2=b_2 \\ & {...} \\ & a_{m1}x_{1}+a_{m2}x_{2}+...+a_{mn}x_{n}+s_m=b_m \\ & x_1,x_2,...,x_n,s_1,...,s_m \geq 0 \end{aligned} maxs.t.Z=c1x1+c2x2+...+cnxna11x1+a12x2+...+a1nxn+s1=b1a21x1+a22x2+...+a2nxn+s2=b2...am1x1+am2x2+...+amnxn+sm=bmx1,x2,...,xn,s1,...,sm≥0
写出矩阵形式
m a x Z = c 1 x 1 + c 2 x 2 + . . . + c n x n s . t . [ a 11 a 12 . . . a 1 n 1 0 . . . 0 a 21 a 22 . . . a 2 n 0 1 . . . 0 . . . . . . . . . . a m 1 a m 2 . . . a m n 0 0 . . . 1 ] [ x 1 x 2 . x n s 1 s 2 . s m ] = [ b 1 b 2 . b m ] x ′ ≥ 0 \begin{aligned} max\quad& Z=c_1x_1+c_2x_2+...+c_nx_n\\ s.t.\quad& \begin{bmatrix} a_{11} & a_{12} & ... & a_{1n} & 1 & 0 & ... & 0\\ a_{21} & a_{22} & ... & a_{2n} & 0 & 1 & ... & 0\\ . & . & . & . & . & . & ... & . \\ a_{m1} & a_{m2} & ... & a_{mn} & 0 & 0 & ... & 1 \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ . \\ x_n\\ s_1\\ s_2\\ .\\ s_m \end{bmatrix}= \begin{bmatrix} b_1 \\ b_2 \\ . \\ b_m\\ \end{bmatrix}\\ & \boldsymbol{x'} \geq0 \\ \end{aligned} maxs.t.Z=c1x1+c2x2+...+cnxn⎣⎢⎢⎡a11a21.am1a12a22.am2..........a1na2n.amn10.001.0............00.1⎦⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡x1x2.xns1s2.sm⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎡b1b2.bm⎦⎥⎥⎤x′≥0
在松弛形式下,原来的 n n n个变量 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn,加上 m m m个松弛变量 s 1 , s 2 , . . . , s m s_1,s_2,...,s_m s1,s2,...,sm变成 n + m n+m n+m个变量,而约束还是 m m m个等式,所以这个方程组是一个欠定线性方程组,是不可能有唯一解的。
可以看到松弛后的系数矩阵 A ′ A' A′是在原系数矩阵上加上 m m m维单位矩阵构成的增广系数矩阵:
A ′ = [ a 11 a 12 . . . a 1 n 1 0 . . . 0 a 21 a 22 . . . a 2 n 0 1 . . . 0 . . . . . . . . . . a m 1 a m 2 . . . a m n 0 0 . . . 1 ] = [ A ∣ I ] A'= \begin{bmatrix} a_{11} & a_{12} & ... & a_{1n} & 1 & 0 & ... & 0\\ a_{21} & a_{22} & ... & a_{2n} & 0 & 1 & ... & 0\\ . & . & . & . & . & . & ... & . \\ a_{m1} & a_{m2} & ... & a_{mn} & 0 & 0 & ... & 1 \\ \end{bmatrix} = [\boldsymbol{A} | \boldsymbol{I}] A′=⎣⎢⎢⎡a11a21.am1a12a22.am2..........a1na2n.amn10.001.0............00.1⎦⎥⎥⎤=[A∣I]
如果 A ′ A' A′是满秩矩阵,即 R a n k ( A ′ ) = m Rank(A')=m Rank(A′)=m,那么也就意味着 A ′ A' A′的 n + m n+m n+m列中最多只会有 m m m列线性无关,也就是说这 m m m列互相之间无法线性组合,而除了这 m m m列之外的系数列,都可以用这 m m m列线性表示;所以这 m m m列其实就是一个 m m m维空间的基底。观察上面定义里的增广矩阵 A ′ A' A′,可以看到后面附加的 m m m维单位矩阵就是线性无关的,所以这个 m m m列的单位矩阵就是一个基底。
相关定理
应用单纯形算法是基于一些基本定理的,这些定理都有严格的数学证明,我们只需要知道就可以:
- 如果线性规划存在可行域,则可行域为凸集
- 线性规划的基可行解对应于可行域的顶点
- 如果线性规划有最优解,则一定存在基可行解(或者说可行域的一个顶点)为最优解
这里提到了一个关键的名词"基可行解",关于它的含义下文会详细描述。
用一个简单的例子来帮助理解:
m a x Z = 40 x 1 + 50 x 2 s . t . x 1 + 2 x 2 ≤ 40 4 x 1 + 3 x 2 ≤ 120 x 1 , x 2 ≥ 0 \begin{aligned} max\quad& Z=40x_1+50x_2\\ s.t.\quad& x_1+2x_2\leq40 \\ & 4x_1+3x_2\leq120 \\ & x_1,x_2\geq0 \end{aligned} maxs.t.Z=40x1+50x2x1+2x2≤404x1+3x2≤120x1,x2≥0
我们可以在二维平面上可以画出它的定义域:
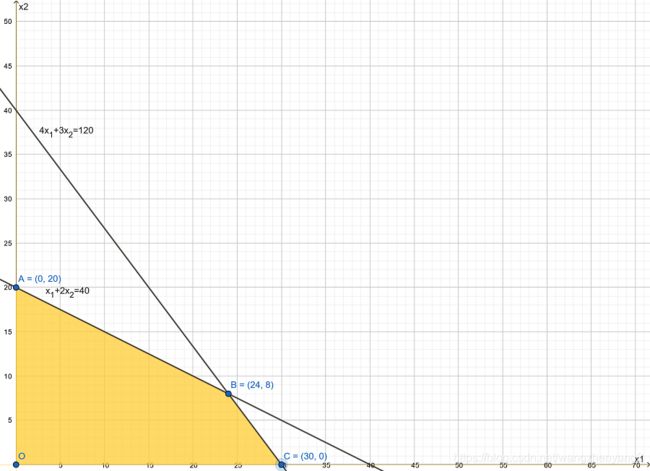
黄色部分就是该问题的可行域,它的边界是一个凸包,有A, B, C和原点O四个顶点,这四个顶点对应的 x 1 , x 2 x1,x2 x1,x2的值都是原问题的可行解,并且顶点 B ( 24 , 8 ) B(24,8) B(24,8)对应的目标值1360是原问题的最优目标值, x 1 = 24 , x 2 = 8 x_1=24,x_2=8 x1=24,x2=8就是原问题的最优解
基变量和基可行解
如上面所述,对于松弛后的规划模型,其系数矩阵 A ′ A' A′及其对应的变量 x ′ \boldsymbol{x'} x′可以写成如下的分块矩阵形式:
A ′ = [ A I ] , x ′ = [ x x b ] \boldsymbol{A'}=[\boldsymbol{A}\quad \boldsymbol{I}],\quad \boldsymbol{x'}=\begin{bmatrix} x\\ x_b\\ \end{bmatrix} A′=[AI],x′=[xxb]
这个表示形式不仅是只可以用在初始的松弛模型,也可以在算法任意的变换过程中进行表示,因为可以对增广系数矩阵进行初等行变换(高斯消元);另外实际的计算过程中并不需要严格按这种形式,这里只是为了帮助理解。在这种表示形式下,我们把单位矩阵 I \boldsymbol{I} I对应的变量部分 x b \boldsymbol{x_b} xb称为基变量,因为单位矩阵的 m m m列线性无关,是一个基底;与之相对的,把 A \boldsymbol{A} A对应的变量部分 x x x称为非基变量
定义基变量和非基变量的目的是为了生成问题的可行解。松弛后的规划问题的约束方程组数量只有 m m m个,但变量有 n + m n+m n+m个,所以如果要从方程组计算出一个解,必须要固定住其中 n n n个变量的值,进而计算出剩下 m m m个变量的值。在定义了基变量和非基变量后,我们令所有的非基变量等于零 x = 0 ⃗ \boldsymbol{x}=\vec{0} x=0,那么剩下的基变量则可以直接得到:
x b = b ⃗ \boldsymbol{x_b}=\vec{b} xb=b
由此得到松弛线性规划的一个解:
x = [ 0 ⃗ b ⃗ ] \boldsymbol{x}= \begin{bmatrix} \vec{0}\\ \vec{b}\\ \end{bmatrix} x=[0b]
我们称这个解为基解,注意基解未必是可行的,为什么呢? 因为在经过高斯消元形成上面的分块矩阵后,等式右侧的 b ⃗ \vec{b} b未必所有元素都大于零,那么基解中就会存在负数分量,这是不满足松弛问题的基本约束的。
如果任意选择 m m m个变量作为基变量,那么存在 C n + m m = C n + m n C_{n+m}^m=C_{n+m}^n Cn+mm=Cn+mn个基解,不过这里面只有部分解能满足都大于零的约束,称这些基解为基可行解,我们的计算目标也就是要找到使得目标函数最大的基可行解
出基入基
单纯形算法的基本过程就是一个在 A \boldsymbol{A} A加上 b \boldsymbol{b} b的增广矩阵上进行高斯消元的迭代过程;每次迭代中, A \boldsymbol{A} A中的一列会被选中,和上个迭代中 I \boldsymbol{I} I的一列进行互换(对应的两个变量则进行行互换操作),重新进行高斯消元,从而得到一个新的基解;迭代的终止条件找到使目标最大的基可行解;并且迭代中采用一些措施来保证每次迭代找到基解都是可行解,这些措施的具体内容本文略过。
我们还是用上面那个例子来理解出基入基的操作:
m a x Z = 40 x 1 + 50 x 2 s . t . x 1 + 2 x 2 ≤ 40 4 x 1 + 3 x 2 ≤ 120 x 1 , x 2 ≥ 0 \begin{aligned} max\quad& Z=40x_1+50x_2\\ s.t.\quad& x_1+2x_2\leq40 \\ & 4x_1+3x_2\leq120 \\ & x_1,x_2\geq0 \end{aligned} maxs.t.Z=40x1+50x2x1+2x2≤404x1+3x2≤120x1,x2≥0
这个问题的松弛形式:
m a x Z = 40 x 1 + 50 x 2 s . t . x 1 + 2 x 2 + s 1 = 40 4 x 1 + 3 x 2 + s 2 = 120 x 1 , x 2 , s 1 , s 2 ≥ 0 \begin{aligned} max\quad& Z=40x_1+50x_2\\ s.t.\quad& x_1+2x_2+s_1=40 \\ & 4x_1+3x_2+s_2=120 \\ & x_1,x_2,s_1,s_2\geq0 \end{aligned} maxs.t.Z=40x1+50x2x1+2x2+s1=404x1+3x2+s2=120x1,x2,s1,s2≥0
这个最初始的松弛形式的约束方程组就对应了一个基变量分块表示形式:
[ 1 2 1 0 4 3 0 1 ] [ x 1 x 2 s 1 s 2 ] = [ 40 120 ] \left[ \begin{array}{cc|cc} 1 & 2 & 1 & 0 \\ 4 & 3 & 0 & 1 \end{array} \right] \begin{bmatrix} x_1\\ x_2\\ s_1\\ s_2 \end{bmatrix}= \begin{bmatrix} 40\\ 120\\ \end{bmatrix} [14231001]⎣⎢⎢⎡x1x2s1s2⎦⎥⎥⎤=[40120]
也就是说变量 s 1 s_1 s1和 s 2 s_2 s2是初始的基变量, x 1 x_1 x1和 x 2 x_2 x2是非基变量,我们将 x 1 = x 2 = 0 x_1=x_2=0 x1=x2=0,从而得到 s 1 = 40 , s 2 = 120 s_1=40,s_2=120 s1=40,s2=120,我们找到了一个最初的基可行解:
x = [ x 1 x 2 s 1 s 2 ] = [ 0 0 40 120 ] \boldsymbol{x}= \begin{bmatrix} x_1\\ x_2\\ s_1\\ s_2 \end{bmatrix}= \begin{bmatrix} 0\\ 0\\ 40\\ 120 \end{bmatrix} x=⎣⎢⎢⎡x1x2s1s2⎦⎥⎥⎤=⎣⎢⎢⎡0040120⎦⎥⎥⎤
并且这个初始解就对应于原始问题定义域上的原点:
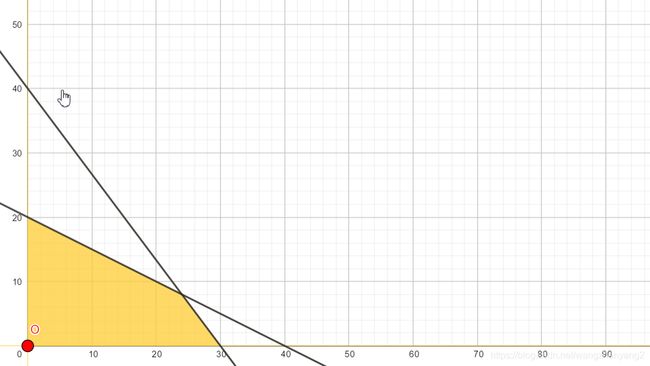
现在我们尝试把变量 x 1 x_1 x1和 s 1 s_1 s1进行"交换",也就是把 s 1 s_1 s1移出基变量组,把 x 1 x_1 x1移入基变量组:

对这个进行了出基和入基变换的增广矩阵进行初等行变换操作:
[ 1 2 1 0 40 0 3 4 1 120 ] ⟹ [ 1 2 1 0 40 − 4 − 5 0 1 − 40 ] \begin{bmatrix} 1 & 2 & 1 & 0 & 40\\ 0 & 3 & 4 & 1 & 120 \end{bmatrix}\\ \Longrightarrow \begin{bmatrix} 1 & 2 & 1 & 0 & 40\\ -4 & -5 & 0 & 1 & -40 \end{bmatrix} [1023140140120]⟹[1−42−5100140−40]
即:
[ 1 2 1 0 − 4 − 5 0 1 ] [ s 1 x 2 x 1 s 2 ] = [ 40 − 40 ] \left[ \begin{array}{cc|cc} 1 & 2 & 1 & 0 \\ -4 & -5 & 0 & 1 \end{array} \right] \begin{bmatrix} s_1\\ x_2\\ x_1\\ s_2 \end{bmatrix}= \begin{bmatrix} 40\\ -40\\ \end{bmatrix} [1−42−51001]⎣⎢⎢⎡s1x2x1s2⎦⎥⎥⎤=[40−40]
由此我们得到了这样一个基解
x = [ x 1 x 2 s 1 s 2 ] = [ 40 0 0 − 40 ] \boldsymbol{x}= \begin{bmatrix} x_1\\ x_2\\ s_1\\ s_2 \end{bmatrix}= \begin{bmatrix} 40\\ 0\\ 0\\ -40 \end{bmatrix} x=⎣⎢⎢⎡x1x2s1s2⎦⎥⎥⎤=⎣⎢⎢⎡4000−40⎦⎥⎥⎤
这里 s 2 s_2 s2小于零,这个解是不可行的,所以我们拿 x 1 x_1 x1和 s 1 s_1 s1来互换是不行的。
我们再试下 x 2 x_2 x2和 x 1 x_1 x1进行出基入基操作:
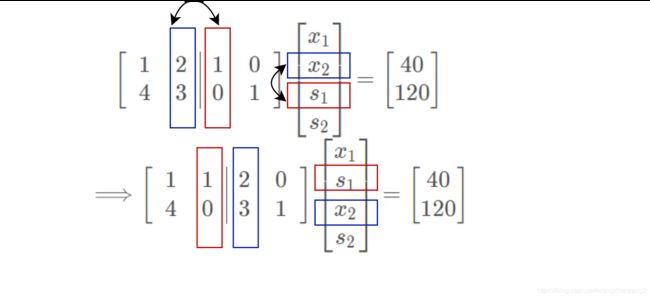
[ 1 1 2 0 40 4 0 3 1 120 ] ⟹ [ 1 1 2 0 40 5 2 − 3 2 0 1 60 ] ⟹ [ 1 2 1 2 1 0 20 5 2 − 3 2 0 1 60 ] \begin{bmatrix} 1 & 1 & 2 & 0 & 40\\ 4 & 0 & 3 & 1 & 120 \end{bmatrix}\\ \Longrightarrow \begin{bmatrix} 1 & 1 & 2 & 0 & 40\\ \frac{5}{2} & -\frac{3}{2} & 0 & 1 & 60 \end{bmatrix}\\ \Longrightarrow \begin{bmatrix} \frac{1}{2} & \frac{1}{2} & 1 & 0 & 20\\ \frac{5}{2} & -\frac{3}{2} & 0 & 1 & 60 \end{bmatrix} [1410230140120]⟹[1251−2320014060]⟹[212521−2310012060]
我们得到了一个基可行解:
x = [ x 1 x 2 s 1 s 2 ] = [ 0 20 0 60 ] \boldsymbol{x}= \begin{bmatrix} x_1\\ x_2\\ s_1\\ s_2 \end{bmatrix}= \begin{bmatrix} 0\\ 20\\ 0\\ 60 \end{bmatrix} x=⎣⎢⎢⎡x1x2s1s2⎦⎥⎥⎤=⎣⎢⎢⎡020060⎦⎥⎥⎤
这个基可行解对应于原始问题定义域上的顶点A,该解的目标值为 40 x 1 + 50 x 2 = 1000 40x_1+50x_2=1000 40x1+50x2=1000;可以看到这样的一个出基入基操作也对应从顶点O移到顶点A的过程;点A还不是最优解,它还需要移到点B上才是最优解:
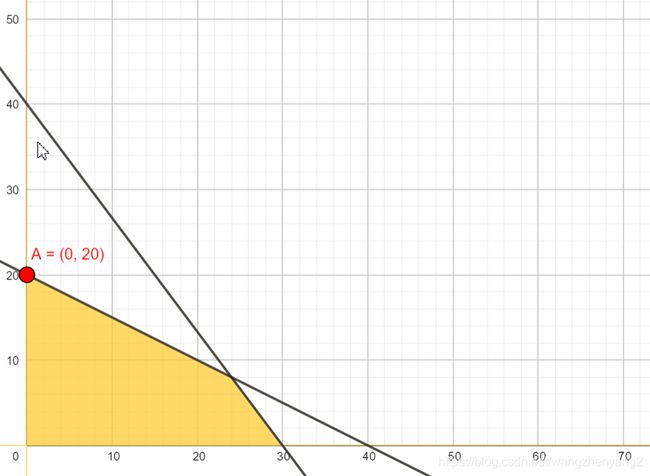
通过这个例子可以看到,在单纯形算法的每次迭代中,有两个很关键的问题需要解决:
- 如何保证出基和入基操作后解的可行性
- 如何判断当前是否到达最优解从而退出算法
这两个点我放到后面一篇文章中叙述。