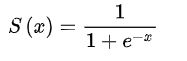人工智能---深度学习神经网络神经元的实现
系列文章目录
人工智能—深度学习从感知机到神经网络
文章目录
- 系列文章目录
- 前言
- 一、神经元的组成
- 二、激活函数的实现
-
- 1.什么是激活函数
- 2.常见的激活函数
- 3.激活函数实现
- 三、神经元实现
-
- 1.初始化参数
- 2.权重设置
- 3.偏置设置
- 4.求和方法
- 5.激活函数
- 6.开始生产我们的第一个神经细胞!
- 总结
前言
我们在上一章中已经了解了神经网络的起源感知机的基本原理和 实现,掌握了小型感知机系统的搭建和测试,其实那样的模型已经很接近我们现代的简单的神经网络模型了。接下来我们将正式进行神经网络的学习和实现。
一、神经元的组成
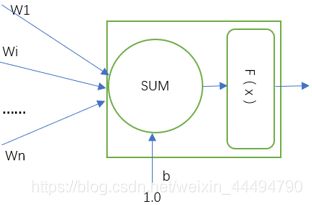
神经元的组成包括 输入、权重、偏置、计算、激活、输出这么几个部分,每一个部分都有着自己独立的作用。
- 输入(Input):输入可能是来自外部数据的投入,也可能是上一个结点的输出数据。输入的个数可以有很多个。
- 权重(Wi):决定了对应输入的重要程度,如果权重为0则相当于断开了这条链接。
- 偏置(b):一个神经元共享一个偏置,他决定了这个神经元被激活的难易程度。
- 计算(f(x)):相当于一个神经元的胞体,他负责对数据进行运算处理。这边举例的是一个求和运算。
- 激活(F(x)):他是模拟了生物电流传播的一个阈值的概念,超过这个阈值的信号强度才能被输出,同时也起到对输出进行整流的作用。
- 输出(Output):经过激活函数激活的数据将被输出,可能是神经网络的终点,也可能是下一个神经元的起点。输出的个数可以有很多个。
二、激活函数的实现
1.什么是激活函数
在感知机中我们已经提到了θ的概念,当时我们用θ来简单的区分0,1信号的阈值,但一个实际神经元的阈值设定要更加灵活,这时一个简单的变量就无法满足多样化的阈值需求了,于是我们引入了激活函数的概念。他的作用就是决定如何来激活输出数据流。
2.常见的激活函数
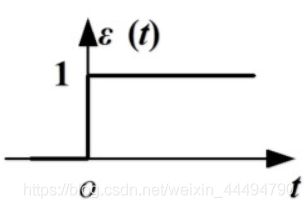
- 阶跃激活函数
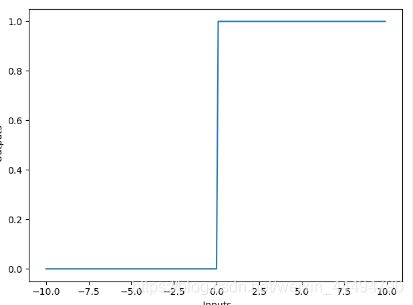
阶跃函数即定义一个阈值,如果超过那个阈值的信号强度都会被定义为1,而低于该阈值的信号强度都会被定义为0。通过阶跃信号来表示复杂的信号,可以简化对复杂信号的一些特性的研究。从而减少计算复杂信号频谱的难度。
其实我们在前面的感知机中已经简单的实现了一个阶跃函数。通过一个阈值θ,不过那里我们是用一个变量来表示的,而这里我们需要将其统一为函数。
- sigmoid函数
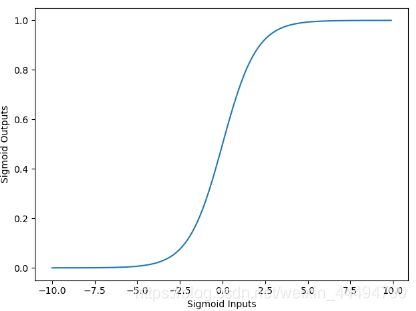
sigmoid函数也叫Logistic函数,他的定义式为
用于隐层神经元输出,取值范围为(0,1),它可以将一个实数映射到(0,1)的区间。在特征相差比较复杂或是相差不是特别大时效果比较好。Sigmoid作为激活函数有以下优缺点:
优点:平滑、易于求导。
缺点:激活函数计算量大,反向传播求误差梯度时,求导涉及除法;反向传播时,很容易就会出现梯度消失的情况,从而无法完成深层网络的训练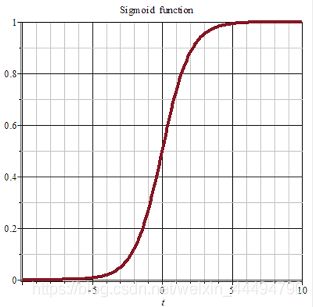
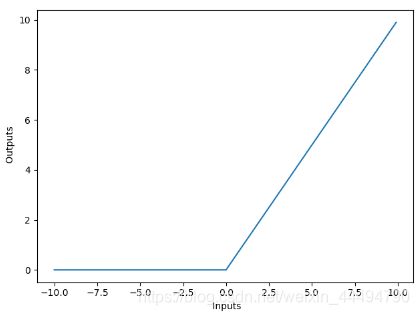
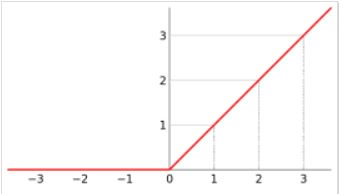
- ReLU函数
这个函数其实毕竟好理解,简单来说就是但小于阈值点时,全部输出0,大于阈值的就输出原值。我们直接从数学角度可能无法理解他比前面的激活函数好在哪,但是从生物学上来说这样的输出规则更符合人脑的网络运行方式。也就是更拟生。
3.激活函数实现
- 阶跃激活函数
def f(x):
return np.array(x>0)
inputs = np.arange(-10,10,0.1)
outputs = f(inputs)
- Sigmoid函数
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1.0/(1+np.exp(-x))
- ReLU函数
import numpy as np
import matplotlib.pyplot as plt
def relu(x):
return np.maximum(0,x)
三、神经元实现
1.初始化参数
class cell():
def __init__(self,x1,x2):
self.output = 0
self.input = [x1,x2]
self.weight1 = 0
self.weight2 = 0
self.bias = 0
2.权重设置
def set_weight(self,weight1,weight2):
self.weight1 = weight1
self.weight2 = weight2
3.偏置设置
def set_bias(self,bias):
self.bias = bias
4.求和方法
def add(self):
self.output = self.weight1*self.input[0]+self.weight2*self.input[1]
return self.activation(self.output)
5.激活函数
def activation(self,input):
return 1.0 / (1 + np.exp(-input))
6.开始生产我们的第一个神经细胞!
a = cell(1,1)
a.set_weight(1,1)
a.set_bias(0)
b = cell(2,2)
b.set_weight(3,2)
b.set_bias(0)
print("a细胞:",a.add())
print("b细胞:",b.add())
a.set_bias(-3)
print("a细胞变偏置:",a.add())
a细胞: 0.8807970779778823
b细胞: 0.9999546021312976
a细胞变偏置: 0.2689414213699951
Process finished with exit code 0
总结
通过感知机的阈值过渡到我们的神经网络激活函数,也是从感知机到我们的神经网络,我们已经生产了我们的第一个神经元细胞,接下来我们要做的就是将他们联系在一起,然后运转我们庞大的神经网络系统。