T-GCN-时间图卷积网络交通速度中的预测
论文原始链接
代码
知乎主页
1:摘要
实时准确的交通预测在智能交通系统中城市交通规划,交通管理和交通控制起着重要的作用和意义。然而,由于城市道路网络拓扑结构的约束和时间的动态变化规律,流量预测一直被认为是一个科学问题,即:空间依赖和时间依赖。为了捕获时空间依赖性,本文提出了T-GCN(temporal graph convolutional network),模型融合了图卷积网络(GCN)和门控递归单元(GRU)。GCN用于学习复杂的拓扑结构来捕获空间依赖关系,GRU用于学习交通数据的动态变化来捕获时间依赖关系。T-GCN模型应用于基于城市路网的交通预测。实验表明T-GCN模型预测结果优于基准模型。
2:文章亮点
- T-GCN模型集成了图卷积网络和门控递归单元。利用图卷积网络捕获路网拓扑结构,对路网空间依赖性进行建模。利用门控递归单元捕获道路交通数据的动态变化,对时间依赖性进行建模。此外,T-GCN模型也可应用于其它时空预测任务。
- T-GCN模型的预测结果表明,T-GCN模型不仅可以实现短期预测,还可以用于长期的交通预测任务(15分钟30分钟45分钟60分钟)
- 真实的交通数据集结果显示,与基线方法相比,该方法的预测误差降低了约1.5%-57.8%,表明了T-GCN模型在交通预测方面的优越性
3:问题描述
3.1:问题定义
定义1
用G表示道路网络,用无权重图G=(V,E)来表示路网拓扑结构,将每个道路抽象为图中的一个节点,V表示节点的集合,用 V = { v 1 , v 2 , ⋯ , v N } V=\left\{v_{1}, v_{2}, \cdots, v_{N}\right\} V={v1,v2,⋯,vN}来表示,其中N表示节点数量,E表示边的集合,邻接矩阵A表示道路之间的连接, A ∈ R N × N A \in R^{N \times N} A∈RN×N,其中1表示两条道路之间是连通的,0表示非连通的。
定义2
特征矩阵 X N × P X^{N \times P} XN×P。道路上的交通信息网络是网络中节点的属性特征, P代表节点属性的数量特征(比如历史时间序列的长度), X t ∈ R N × i X_{t} \in R^{N \times i} Xt∈RN×i表示在时刻 i 的每条道路速度,。节点属性特性可以是任何交通信息,比如交通速度、交通流和交通密度。
因此,时空交通预测问题可以认为:在给定路网拓扑G和特征矩阵X的前提下,学习映射函数f,然后计算预测未来T时刻的交通信息,如下公式所示:
[ X t + 1 , ⋯ , X t + T ] = f ( G ; ( X t − n , ⋯ , X t − 1 , X t ) ) \left[X_{t+1}, \cdots, X_{t+T}\right]=f\left(G ;\left(X_{t-n}, \cdots, X_{t-1}, X_{t}\right)\right) [Xt+1,⋯,Xt+T]=f(G;(Xt−n,⋯,Xt−1,Xt))
其中n表示历史时间序列长度,T表示预测的时间序列长度。
4:模型总结介绍
T-GCN模型由图卷积网络和门控递归单元两部分组成。如下图所示,首先使用历史n时间序列数据作为输入,利用图卷积网络(GCN)捕获路网拓扑结构信息来获取空间特征。然后,将得到的具有空间特征的时间序列输入门控递归单元(GRU)模型,通过单元间的信息传递获得动态变化,捕捉时间特征。最后,通过全连通层得到结果。
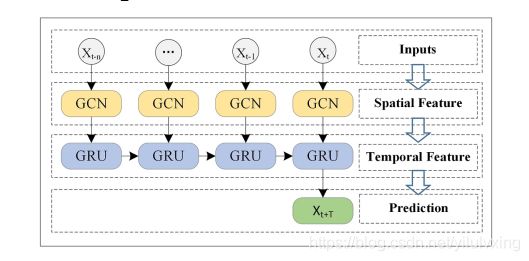
4.1:空间依赖性建模
交通道路拓扑结构是图的形式,因此采用GCN来捕获捕捉空间依赖关系。
给定一个邻接矩阵A和特征矩阵X, GCN模型在傅里叶域中构造一个过滤器。该滤波器作用于图的节点上,通过它的一阶邻域捕获节点之间的空间特征,然后通过叠加多个卷积层来构建GCN模型(这里就和很多paper中的解释定义类似),可以表示为:

该篇论文选择2层GCN模型捕捉空间依赖关系,可以表示为:
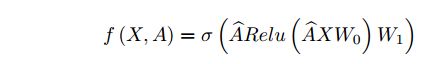
其中X表示特征矩阵,A表示邻接矩阵, A ^ = D ~ − 1 2 A ~ D ~ − 1 2 \widehat{A}=\widetilde{D}^{-\frac{1}{2}} \widetilde{A} \tilde{D}^{-\frac{1}{2}} A =D −21A D~−21表示计算处理过程, A ~ = A + I N \widetilde{A}=A+I_{N} A =A+IN表示邻接矩阵和自连接过程, D ^ \widehat{D} D 表示度矩阵, D ~ = ∑ j A ~ i j . W 0 \widetilde{D}=\sum_{j} \widetilde{A}_{i j} . W_{0} D =∑jA ij.W0和 W 1 W_{1} W1表示第一层和第二层的权重矩阵。
然后,文章使用图卷积网络GCN模型学习空间特征。如下图所示,文章指出:假设节点1为中心道路,GCN模型可以得到中心道路与其周围道路之间的拓扑连接关系,对路网拓扑结构和道路属性进行编码,最终学习空间依赖关系。
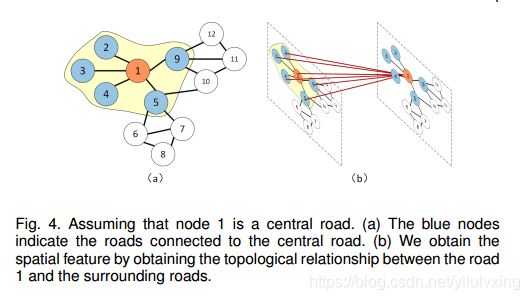
4.2:时间依赖性建模
文章采用GRU来学习时间依赖关系。由于LSTM结构复杂,训练时间较长,相对地,GRU参数较少,训练能力较少,GRU结构如下图。
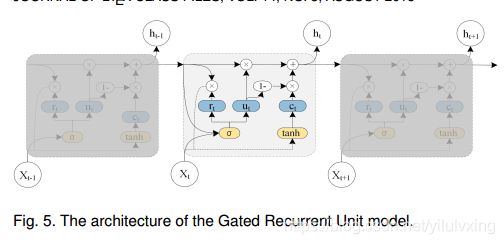
4.3:时空建模
如下图所示,文章指出左边是时空预测的过程,右侧的是T-GCN cell的特定结构, ht−1表示t – 1时刻的输出, GC是图卷积过程, ut 和 rt是t时刻的更新门和重置门, ht表示t时刻的输出。(简单来说就是叠加了两个GCN层和一个GRU层)。
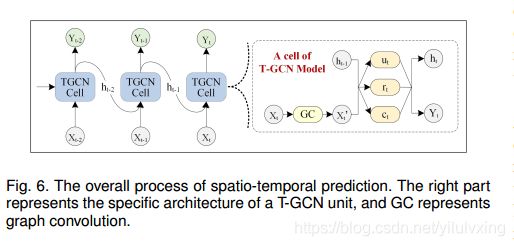
4.4:损失函数
文章指出,为了防止过拟合,在损失函数中添加了正则项:
loss = ∥ Y t − Y ^ t ∥ + λ L r e g =\left\|Y_{t}-\widehat{Y}_{t}\right\|+\lambda L_{r e g} =∥∥∥Yt−Y t∥∥∥+λLreg
5:评价指标
作者一共选取了5个评价指标:RMSE、MAE、ACC、R2、VAR。5个指标中,RMSE和MAE用于测量预测误差,数值越小模型效果越好。Accuracy用于检测预测精度,数值越大模型效果越好。R2和var计算相关系数,衡量预测结果代表实际数据的能力,值越大模型效果越好。
6:超参数设置
T-GCN模型的超参数主要包括:
- 学习速度
- 批量大小
- 训练时间
- 隐藏单元数
文章指出,学习率大小为0.001,批量大小为32,训练时间为5000,隐藏单元数是T-GCN模型的一个非常重要的参数,不同的隐藏单元数对预测精度有很大的影响。为了选择最优值,对不同的隐藏单元数量进行了实验,从而选择最优值。在实验中,对于测试数据集,分别从[8,16,32,64,100,128]中选择隐藏单元的个数,分析预测精度的变化。根据实验结对测试数据集设置了100个隐藏单元。同样地,对另一个测试数据集设置了64隐藏单元。其中优化器选取的是Adam用于训练T-GCN模型。
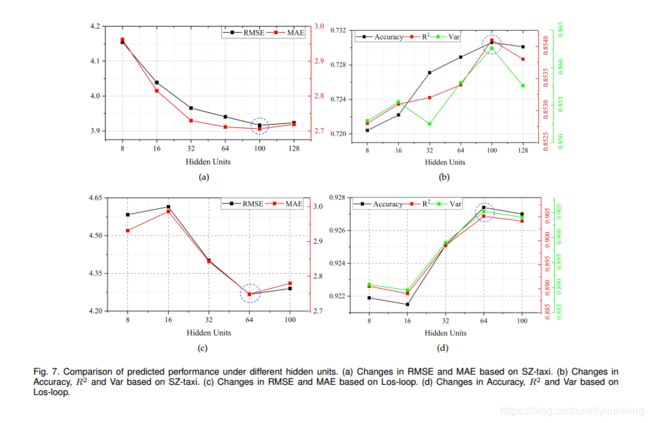
此外,作者为了检验T-GCN是否真的具有捕获时空依赖关系的能力,将T-GCN单独与GRU 进行比较,从下图的RMSE指标结果中,可以看到T-GCN较于GRU具有明显的优势。
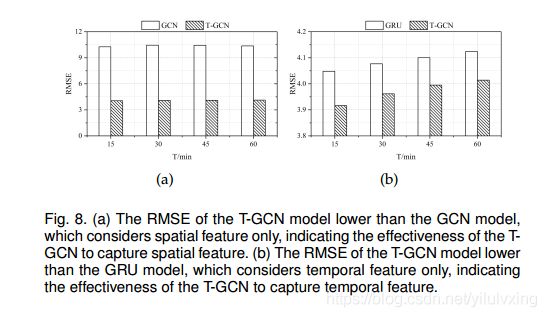
最后,作者通过对比预测时间序列的长度大小,发现T-GCN无论是在短时预测还是长时预测中,均具有较好的表现效果,表明T-GCN即可用于短时预测,也可以用于长时预测。测试结果如下图所示:
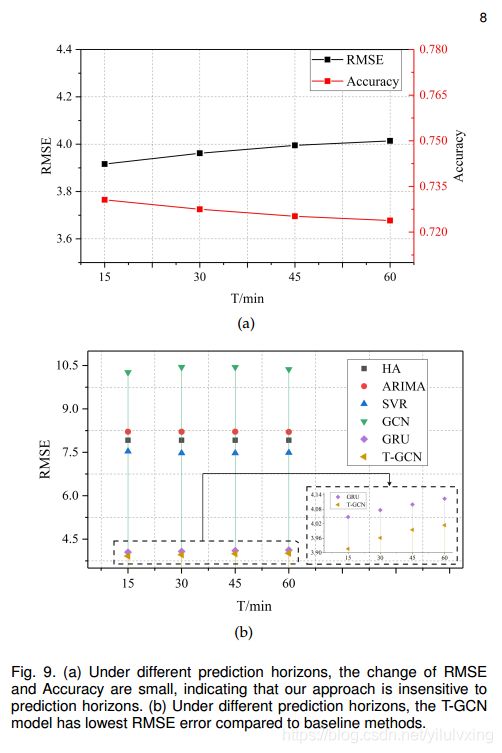
知乎主页