【翻译+笔记】ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks
（因为没本事解读数学推导于是只能整了一份加笔记的翻译）
ECA-Net:深度卷积神经网络的有效通道注意
ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks 论文开源代码
文章总结
ECA-Net是基于SE-Net的扩展，作者认为SE block的两个FC层之间的降维是不利于channel attention的权重学习的，权重学习的过程应该直接一一对应。作者做了一系列实验来证明在attention block中保持channel数不变的重要性。
ECA-Net的做法为：
- Global Avg Pooling得到一个 1 ∗ 1 ∗ C 1∗1∗C 1∗1∗C的向量；
- 通过一维卷积来完成跨通道的信息交互。
其中一维卷积的卷积核大小通过一个函数来自适应，使得channel数较大的层可以更多地进行跨通道交互。自适应卷积核大小的计算公式为： k = ψ ( C ) = ∣ log 2 ( C ) γ + b γ ∣ k=\psi(C)=|\frac{\log_2(C)}{\gamma}+\frac {b}{\gamma}| k=ψ(C)=∣γlog2(C)+γb∣，其中 γ = 2 , b = 1 γ = 2 , b = 1 γ=2,b=1
1.介绍
最近，将通道注意力纳入卷积块已经引起了很多人的兴趣，在性能改进方面显示出巨大的潜力。其中一个代表性的方法是挤压和激发网络（SENet），它为每个卷积块学习通道注意力，为各种深度CNN架构带来明显的性能提升。
在SENet[14]中设置了挤压（即特征聚集）和激发（即特征重新校准）后，一些研究通过捕捉更复杂的通道依赖性或与额外的空间注意力相结合来改进SE块。虽然这些方法取得了较高的精度，但它们往往带来了较高的模型复杂性，并遭受了较重的计算负担。与上述以更高的模型复杂性为代价获得更好的性能的方法不同，本文着重讨论一个问题。能否以更有效的方式学习有效的通道注意？
要回答这个问题，我们先来重温一下SENet中的频道关注模块。具体来说，给定输入features，SE块首先为每个通道独立地采用全局平均池，然后使用两个具有非线性的全连接(FC)层，后面跟随Sigmoid函数来生成通道权重。这两个FC层被设计成捕获非线性跨通道交互，这涉及用于控制模型复杂性的维度减少。虽然这种策略在后续的频道关注模块中被广泛使用[33，13，9]，但我们的实证研究表明，降维会对频道关注预测带来副作用，并且捕获所有频道的依赖关系是低效和不必要的。
因此，本文提出了一种面向深度CNN的高效通道注意(ECA)模块，该模块避免了降维，并以高效的方式捕获跨通道交互。
ECA-Net的结构如下图所示：
- global avg pooling产生1 ∗ 1 ∗ C大小的feature maps；
- 计算得到自适应的kernel_size；
- 应用kernel_size于一维卷积中，得到每个channel的weight。
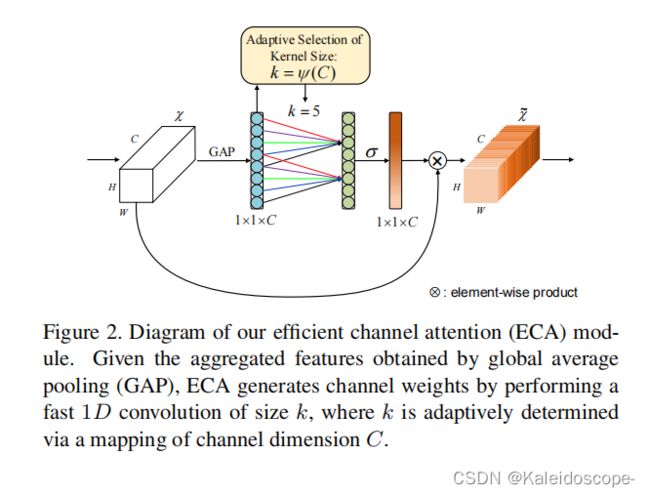
如图2所示，在没有降维的通道式全局平均池化之后，ECA通过处理每个通道及其k个邻居来捕获局部跨通道交互。实践证明，这种方法既能保证效率，又能保证效果。
注意，ECA可以通过大小为k的快速1维卷积来有效地实现，其中核大小k表示局部跨通道交互的覆盖，即有多少邻居参与一个通道的注意力预测。
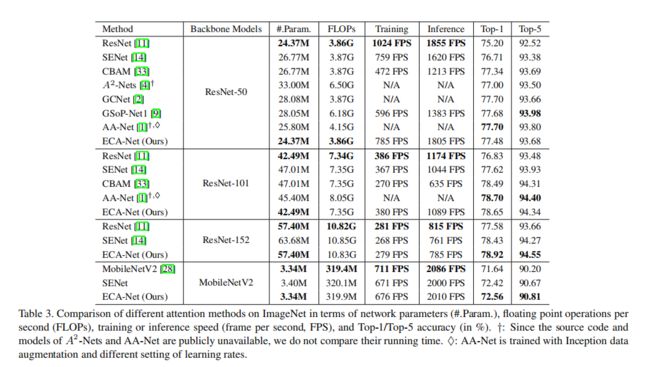
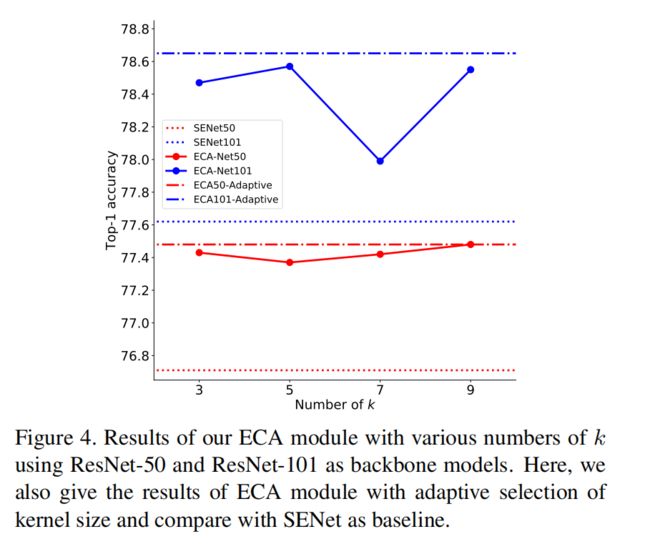
为了避免通过交叉验证来手动调整k，我们开发了一种自适应地确定k的方法，其中交互的覆盖范围(即，内核大小k)与信道维度成比例。如图1和表3所示，与骨干模型[11]相反，采用ECA模块的深度CNN(称为ECA-Net)引入了非常少的额外参数和可以忽略的计算，同时带来了显著的性能提升。
例如，对于24.37M参数和3.86 GFLOPs的ResNet-50，ECA-Net50的附加参数和计算量分别为80和4.7e-4 GFLOPs；同时，ECA-Net50在顶级准确性方面比ResNet-50高出2.28%。
表1总结了现有的注意模块，包括是否存在通道降维（DR）、交叉通道交互和轻量级模型看到我们的ECA模块学习有效的渠道注意通过避免信道降，同时以极其轻量级的方式捕获跨信道交互。为了评估我们的方法，在ImageNet1K [6]和 MS COCO [23]上使用不同的深度CNN架构在各种任务中进行了实验。
本文的贡献总结如下。
1.分析了SE块，并通过经验证明了避免降维和适当的跨通道交互作用分别是学习有效和有效的通道注意的重要因素。
2.基于上述分析，我们试图通过提出高效通道注意（ECA）来开发一个针对深度CNN的极轻便的通道注意模块，该模块很少增加模型的复杂性，同时带来明显的改进。
3.在 ImageNet-1K 和 MS COCO 上的实验结果表明，我们的方法比最先进的方法具有更低的模型复杂性，同时取得了非常有竞争力的性能。
2.相关工作
注意机制已被证明是增强深度学习网络的一种可能的手段。SE-Net [14]首次提出了一种有效的通道注意学习机制，并取得了良好的性能。
随后，注意模块的发展大致可以分为两个方向：
(1)特征聚合的增强；
(2)通道和空间注意的结合。
具体来说：
- CBAM [33]同时采用了平均池和最大池来聚合特征。
- GSoP[9]引入了二阶池化，以实现更有效的特征聚合。
- GE [13]利用深度卷积[5]来探索空间扩展。
- CBAM [33]和scSE [27]使用核大小 k×k 的二维卷积来计算空间注意，然后将其与通道注意力相结合。
- GCNet [2]与非本地（Non-Local,NL）神经网络[32]有着相似的理念，开发了一个简化的NL网络，并与SE块集成，从而产生一个轻量级模块来建模远程依赖。
- 双重注意网络（Double Attention Networks, A 2 A^2 A2-Nets）[4]引入了一种新的NL 块的关系函数，用于图像或视频识别。
- 双注意网络（Dual Attention Network,DAN）[7]同时考虑基于NL的信道和空间注意进行语义分割。
然而，以上大多数基于NL的注意模块由于其模型复杂性高，只能在单个或几个卷积块中使用。显然，以上所有的方法都侧重于开发复杂的注意力模块，以获得更好的性能。与他们不同的是，我们的ECA旨在学习具有低模型复杂度的有效通道注意力。我们的工作也与有效的卷积有关是为轻量级的cnn而设计的。两种广泛使用的有效卷积方法是群卷积[37,34,16]和深度可分离卷积[5,28,38,24]。如表2所示，虽然这些有效卷积涉及的参数较少，但它们在注意模块中的效果很少。
我们的ECA模块旨在捕获局部跨信道交互，它与信道局部卷积[36]和信道级卷积[8]有一些相似之处；与它们不同的是，我们的方法研究了 一个具有自适应核大小的一维卷积来取代信道注意模块中的FC层。与群卷积和深度可分离卷积相比，该方法在较低的模型复杂度的情况下获得了更好的性能。
3.建议的方法
在本节中，我们首先重新讨论SENet中的通道注意模块。然后，通过分析降维和跨通道交互作用的影响，对SE块进行了经验性的诊断。
3.1 对SE模块的通道注意力机制的再现
设一个卷积块的输出为 X ∈ R W × H × C X∈R^{W×H×C} X∈RW×H×C ，其中W、H和C为宽度、高度和通道尺寸(i.e.,过滤器的数量）。因此，SE块中通道的权值可以计算为：
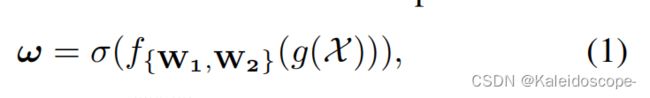
其中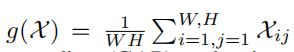
是通道级的全局平均池化（GAP），a是一个Sigmoid函数。使得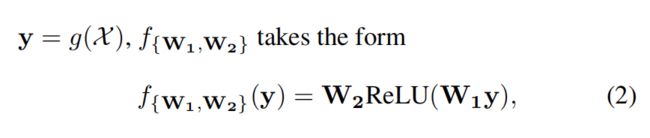
ReLU表示校正的线性单位[25]。
为了避免高模型复杂度，大小为W1和W2 分别被设置为C×(C/r)和C/r)×C。我们可以看到$ f { W 1 , W 2 } f_{\{W1,W2\}} f{W1,W2} 涉及到通道注意块的所有参数。而在等式中的降维性(2)可以降低模型的复杂度，它破坏了信道与其权值之间的直接对应关系。 例如，一个FC层使用所有通道的线性组合来预测每个通道的权重。但等式(2)首先将通道特征投射到一个低维空间中，然后将它们映射回来，使通道与其权重之间的对应关系是间接的。
3.2.高效通道注意（ECA）模块
作者对SE块经验性地分析了通道降维和跨通道交互作用对通道注意学习的影响，提出了高效通道注意（Efficient Channel Attention，ECA）模块。
3.2.1.避免降维
如上所述，在等式中的降维(2)使通道及其权重之间的对应关系是间接的。为了验证其效果，我们将原始的SE块与它的三个变体（即SE-Var1、SE-Var2和SEVar3）进行了比较，所有这些变体都不进行降维。
作者对SE-Net的扩展尝试如下图所示：【前提知识y为平均池化层的输出】，
SE-Var1（直接对y进行非线性运算），
SE-Var2（对y进行depth-wise卷积运算，即一个channel一个参数），
SE-Var3（对y直接进行一个全连接运算），SE-GC（对y进行分组卷积运算），
ECA-NS（每个channel使用k个参数进行channel之间的交互），
ECA（共享k个参数，进行channel之间的交互，即一维卷积）。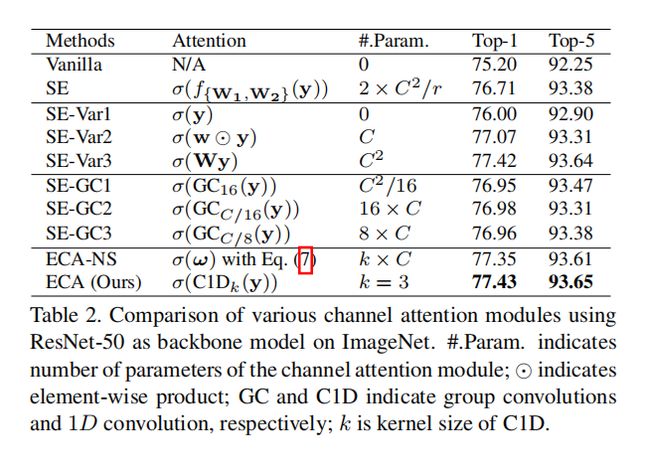
从表2可以得出以下结论，
- SE-Var1与Vanilla的结果表明，不添加参数的attention都是有效的；
- SE-Var2与SE的结果表明，尽管SE-Var2的参数较少，但SE-Var2的效果仍比原始的SE要好，这表明了维持通道数的重要性。这个重要性比考虑channel之间的信息交互依赖的非线性还要重要；
- SE-Var3与SE的结果表明，SE-Var3只是用一个FC都比带维度缩减的两个FC层的SE要好；
- SE-Var3与SE-Var2的结果表明，跨channel的信息交互对于学习channel attention的重要性；
- Group Conv的使用是SE-Var3和SE-Var2的一个折中方法，但使用了Group Conv并没有SE-Var2的效果好；这可能是由于Group Conv放弃了不同Group之间的依赖，因而导致了错误的信息交互；
- ECA-NS对于每个channel都有k个参数，这样可以避免不同Group之间的信息隔离问题，从结果来说是可以的；
- ECA使用共享权重，结果表明了该方法的可行性；同时，共享权重可以减少模型参数；
3.2.2局部跨通道交互
（我先放一个原文在这里，万一译的不对或者说的不对观众老爷可以自行对照参考）
给定聚合特征 y ∈ R C y∈R^C y∈RC如果不进行降维，通道注意就可以通过
进行学习。其中，W是一个C×C参数矩阵。特别是对于SE-Var2和SE-Var3，有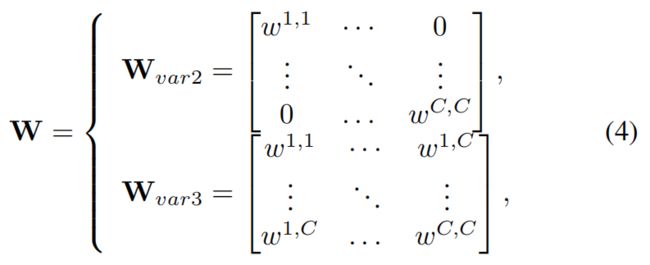
其中 W v a r 2 W_{var2} Wvar2对于SE-Var2是一个对角矩阵，涉及C参数； W v a r 3 W_{var3} Wvar3 对于SE-Var3是一个完整的矩阵，涉及C×C参数。如等式所示(4)，SE-Var3比SE-Var2效果更佳的原因在于，SE-Var3捕捉了通道间的交互关系，而SE-Var2没有。但代价就是SE-Var3使得参量大大增加。
SE-Var2和SE-Var3之间的一个可能的处理办法是 W v a r 2 W_{var2} Wvar2到一个块对角线矩阵，i。e.,
其中等式(5)将通道分为G组，G组包括C/G通道，独立学习各组的通道注意，以局部方式捕获跨通道交互。因此，它涉及 C 2 / G C^2/G C2/G参数。从卷积的角度来看，SE-Var2， SEVar3和等式(5)可以看作是深度可分离卷积、FC层和群卷积。这里，具有群卷积的SE块（SE-GC）表示为 σ ( G C G ( y ) ) = σ ( W G y ) σ(GC_G(y)) = σ(W_Gy) σ(GCG(y))=σ(WGy).然而，如[24]所示，过度的群卷积会增加内存访问成本，从而降低计算效率。此外，如表2所示，不同组的SE-GC对SE-Var2没有增益，这表明它不是捕获局部跨通道交互的有效方案。原因可能是SE-GC完全抛弃了不同组之间的依赖关系。
在本文中，我们探索了另一种捕获局部跨通道交互的方法，以保证效率和有效性。具体来说，我们使用了一个频带矩阵 W k W_k Wk去学习渠道的注意力，
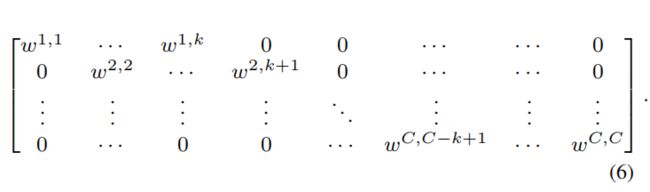
显然， W k W_k Wk在等式(6)涉及k个C参数，通常小于等式的参 数(5)。此外，等式(6)避免了等式中不同群体之间的完全独立(5)。如表2所示，在等式中的方法(6)（即ECA-NS）的性能优于等式的SE-GC(5)。对于等式(6)， y i y_i yi的权重是通过只考虑 y i y_i yi和它的k个邻居得出的，即，
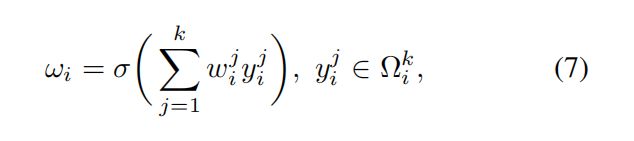
这里的 Ω i k Ω^k_i Ωik表示y的k个相邻通道的集合 y i y_i yi.一个更有效的方法是让所有的渠道共享相同的学习参数，即：
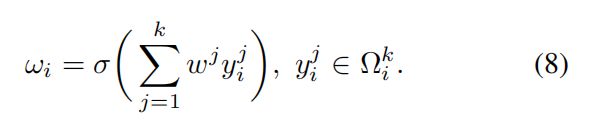
请注意，这种策略可以很容易地通过一个核大小为k的快速一维卷积来实现，即：
其中C1D表示一维卷积。这里是等式中的方法(9)由有效通道注意（ECA）模块调用，它只涉及k个参数。如表2所示，我们使用k = 3的ECA模块在模型复杂度更低的情况下获得了类似的SE-var3的结果，通过适当地捕获局部跨通道交互，保证了效率和有效性。
3.2.3局部跨通道相互作用的覆盖范围
由于我们的ECA模块(9)的目标是适当地捕获局部跨通道交互，所以交互的覆盖范围(i。e., 一维卷积的核大小k)需要确定。在不同的CNN架构中，对于具有不同通道数的卷积块，可以手动调整优化的交互覆盖率。然而，通过交叉验证进行手动调优将花费大量的计算资源。群卷积已经成功地采用改进CNN架构[37,34,16]，其中高维（低维）信道涉 及长距离（短距离）卷积。有着相似的哲学，互动的覆盖范围是合理的。e., 一维卷积的核大小k)与信道维数C 成正比。换句话说，在k和C之间可能存在一个映射：
最简单的映射是一个线性函数， ɸ ( k ) = γ ∗ k − b ɸ(k) = γ*k-b ɸ(k)=γ∗k−b. 然而，以线性函数为特征的关系就太有限了。另 一方面，众所周知，通道维数C (滤波器的数量) 通常被设置为2。因此，我们通过将线性函数 ɸ ( k ) = γ ∗ k − b ɸ(k) = γ*k-b ɸ(k)=γ∗k−b扩展到非线性函数，引入了一个可能的解，即：
然后，给定通道维数C，核大小k可以自适应地得出：
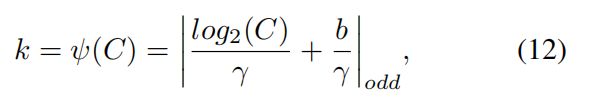
其中|t|表示t的最接近的奇数。在本文中，我们在所有实验中分别将V和b设为2和1。显然，通过映射，高维通道具有更长范围的相互作用，而低维通道通过使用非线性映射进行更短范围的相互作用。
3.3.用于深度cnn的ECA模块
图2说明了我们的ECA模块的概述。ECA模块使用不降维的GAP聚合卷积特征后，首先自适应地确定核大小k，然后进行一维卷积，然后使用Sigmoid函数来学习信道注意。为了 将我们的ECA应用到深度cnn中，我们用与[14]中相同配置的ECA模块替换SE块。所得到的网络由ECA-Net命名。 图3给出了我们的ECA的PyTorch代码。
4.实验
（懒得译了，简单总结一下）
- ECA-Net应用于各种框架的性能展示：
- kernel_size的手动选择实验：
附录
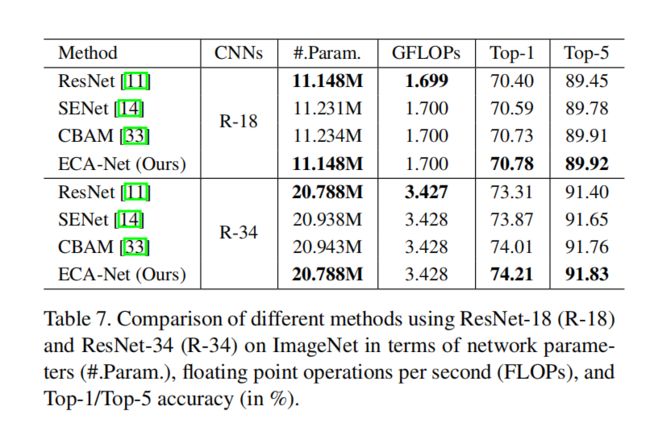
附录一：在ImageNet上使用ResNet-18和ResNet-34的不同方法的比较
附录二：在ECA模块中叠加更多的一维卷积
直观地说，由于建模能力的提高，在ECA模块中堆积更多的一维卷积可能会带来进一步的改进。实际上，我们发现一个额外的一维卷积会带来微不足道的收益(0.1%) ，代价是复杂性略有增加，但更多的一维卷积会降低性能，这可能是由于更多的一维卷积使梯度反向传播更加困难。因此，我们最终的ECA模块只包含一个一维卷积。
附录三：通过ECA模块和SE块学习到的权重的可视化
为了进一步分析我们的ECA模块对学习通道注意的影响 ，我们将学习到的权重可视化
（懒得一张张截高清大图，意会一下吧）
