c#解微分方程_使用C＃开发符号表达库。 微分，简化，方程求解等

c#解微分方程

Why does programming a calculator seem to be a task, which every beginner undertakes? History might have the answer — computers were created for this exact purpose. Unlike the beginners, we will develop a smart calculator, which, although won't reach the complexity of SymPy, will be able to perform such algebraic operations as differentiation, simplification, and equations solving, will have built-in latex support, and have implemented features such as compilation to speed up the computations.

为什么对计算器进行编程似乎是每个初学者都要完成的任务？ 历史可能会给出答案-计算机就是为此目的而创建的。 与初学者不同，我们将开发一个智能计算器，该计算器虽然不会达到SymPy的复杂性，但将能够执行微分，简化和方程求解等代数运算，并具有内置的乳胶支持并具有已实现的功能(例如编译)以加快计算速度。

关于哪些文章？ (What are the articles about?)

repository link存储库链接

Let's do it!

我们开始做吧！

本文适用于谁？ (Whom is this article for?)

对于已经看过的人 (To those who have already seen it)

first and 第一部分和 second parts. 第二部分的翻译。

表达组装 (Expression assembly)

我小时候... (When I was a child...)

什么是表情？ (What is an expression?)

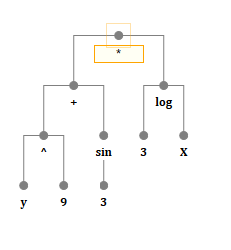
An expression is not a string. It is pretty obvious that a mathematical formula is either a tree or a stack, as it is shown in the example below. Each node of this tree is some kind of an operation, a variable, or a constant.

表达式不是字符串。 显而易见，数学公式可以是树，也可以是堆栈，如下面的示例所示。 该树的每个节点都是某种运算，变量或常量。

Each operation is either a function or an operator, which are actually similar to each other. Their children are the arguments of the respective functions/operators.

每个操作实际上都是彼此相似的函数或运算符。 他们的孩子是各自职能/经营者的观点。

代码中的类层次结构 (Class hierarchy in your code)

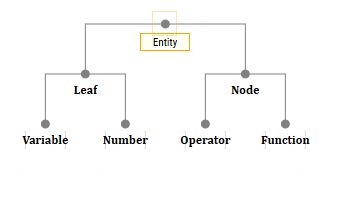
Of course, the implementation can widely vary. However, the idea is that if your tree only consists of nodes and leaves, then despite their differences from each other, they all are generalized by something. I call these «things» — entities. Therefore, the upper class will be the abstract class Entity.

当然，实现方式可以有很大的不同。 但是，这种想法是，如果树仅由节点和叶子组成，那么尽管它们彼此有所不同，但它们都被某种东西概括了。 我称这些“事物”为实体。 因此，上层类将是抽象类Entity。

抽象？ (Abstract?)

And there will also be four child classes: NumberEntity, VariableEntity, OperatorEntity, FunctionEntity.

并且还将有四个子类：NumberEntity，VariableEntity，OperatorEntity，FunctionEntity。

如何构建表达式？ (How to build an expression?)

We will start with building an in-code expression, i.e.

我们将从构建一个代码内表达式开始，即

var x = new VariableEntity("x");
var expr = x * x + 3 * x + 12;

If you declare an empty class VariableEntity, then such a code will throw an exception, something like «I don't know how to multiply and add.»

如果您声明一个空的类VariableEntity，则此类代码将引发异常，例如“我不知道如何相乘和相加”。

优先运算符 (Overriding Operators)

Is a very important and useful feature of most languages, it allows you to customize the execution of arithmetic operations. It is syntactically implemented differently depending on the language. For example, an implementation in C#

这是大多数语言中非常重要和有用的功能，它允许您自定义算术运算的执行。 根据语言的不同，它在语法上的实现方式也不同。 例如，在C＃中的实现

public static YourClass operator +(YourClass a, YourClass b) {
    return new YourClass(a.ToString() + b.ToString());
}

Learn more about overriding statements in C# 了解有关C＃中的覆盖语句的更多信息

My implementation is here.

我的实现在这里 。

(Ex | Im)伪型铸造 ((Ex|Im)plicit type casting)

In compilable languages like C#, such a thing is usually present and allows you to cast the type if necessary without an additional call of myvar.ToAnotherType(). So, for example, it would be more convenient to write

在像C＃这样的可编译语言中，通常会出现这种情况，并允许您在必要时myvar.ToAnotherType()类型，而无需额外调用myvar.ToAnotherType() 。 因此，例如，编写起来会更方便

NumberEntity myvar = 3;

Instead of the usual

而不是通常的

NumberEntity myvar = new NumberEntity(3);

More on type casting in C# 有关C＃中类型转换的更多信息

My implementation here.

我的实现在这里 。

悬挂式 (Hanging)

The Entity class has a Children field — this is just a list of instances of Entity, which are the arguments for this entity.

Entity类具有一个Children字段-这只是Entity实例的列表，这些实例是该实体的参数。

思想 (Thoughts)

When we call a function or operator, we should create a new entity, and put in it the children from which the function or operator is called. For example, the add operator in theory should look something like this:

当我们调用一个函数或操作符时，我们应该创建一个新实体，并在其中放入从中调用该函数或操作符的子级。 例如，理论上的add运算符应如下所示：

public static Entity operator +(Entity a, Entity b){ 
    var res = new OperatorEntity("+");
    res.Children.Add(a);
    res.Children.Add(b);
    return res;
}

That is, now if we have entity x and entity 3, then x + 3 will return the entity of the sum operator with two children: 3 and x. So, we can build expression trees.

也就是说，现在如果我们拥有实体x和实体3，则x + 3将返回具有两个子代的和运算符的实体：3和x。 因此，我们可以构建表达式树。

A function call is simpler and not as beautiful as that with an operator:

函数调用更简单，并且不如运算符那么漂亮：

public Entity Sin(Entity a)
{
    var res = new FunctionEntity("sin");
    res.Children.Add(a);
    return res;
}

My implementation is here.

我的实现在这里 。

Ok, we made up an expression tree.

好的，我们组成了一个表达式树。

变量替代 (Variable substitution)

Everything is extremely simple here. We have Entity — we check whether it is a variable itself; if so, we return the value, otherwise we run through the children.

这里的一切都非常简单。 我们拥有实体-我们检查它本身是否为变量； 如果是这样，则返回该值，否则我们将遍历子级。

In this «huge» 48-line file implements such a complex function.

在此 “巨大的” 48行文件中，实现了如此复杂的功能。

价值计算 (Value calculation)

Yeah, the calculator must calculate. Here we are supposed to add some kind of method to Entity

是的，计算器必须计算。 在这里，我们应该向实体添加某种方法

public Entity Eval()
{
    if (IsLeaf)
    {
        return this;
    }
    else
        return MathFunctions.InvokeEval(Name, Children);
}

The leaf is unchanged, but for everything else we have a custom calculation. Once more, I will only provide an example:

叶子没有变化，但是对于其他所有内容，我们都有自定义计算。 再一次，我仅提供一个示例：

public static Entity Eval(List args)
{
    MathFunctions.AssertArgs(args.Count, 1);
    var r = args[0].Eval();
    if (r is NumberEntity)
        return new NumberEntity(Number.Sin((r as NumberEntity).Value));
    else
        return r.Sin();
}

If the argument is a number, then we perform a numerical operation, otherwise we will return the arguments as they were.

如果参数是数字，则执行数字运算，否则将按原样返回参数。

数？ (Number?)

This is the simplest unit, number. Arithmetic operations can be performed on it. By default, it is complex. It also has operations such as Sin, Cos, and some others.

这是最简单的单位，数字。 可以对其执行算术运算。 默认情况下，它很复杂。 它还具有Sin，Cos等一些操作。

If you are interested in its implementation, Number is described here.

如果您对它的实现感兴趣，请在此处描述Number。

衍生物 (Derivative)

Anyone can calculate the derivative numerically, and such a function is written truly in one line:

任何人都可以数值计算导数，并且这样的函数可以真正地写成一行：

public double Derivative(Func f, double x) => (f(x + 1.0e-5) - f(x)) * 1.0e+5;

But of course we want an analytical derivative. Since we already have an expression tree, we can recursively replace each node in accordance with the differentiation rule. It should work something like this:

但是，我们当然需要解析导数。 由于我们已经有了一个表达式树，因此我们可以根据差异规则递归替换每个节点。 它应该像这样工作：

I realized it in the following way:

我是通过以下方式实现的：

public static Entity Derive(List args, VariableEntity variable) {
    MathFunctions.AssertArgs(args.Count, 2);
    var a = args[0];
    var b = args[1];
    return a.Derive(variable) + b.Derive(variable);
}

Product:

产品：

public static Entity Derive(List args, VariableEntity variable)
{
    MathFunctions.AssertArgs(args.Count, 2);
    var a = args[0];
    var b = args[1];
    return a.Derive(variable) * b + b.Derive(variable) * a;
}

And here is a workaround in itself:

这本身就是一种解决方法：

public Entity Derive(VariableEntity x)
{
    if (IsLeaf)
    {
        if (this is VariableEntity && this.Name == x.Name)
            return new NumberEntity(1);
        else
            return new NumberEntity(0);
    }
    else
    return MathFunctions.InvokeDerive(Name, Children, x);
}

This is the Entity method. As we see, the leaf has only two states: either it is a variable by which we differentiate, then its derivative is 1, or it is a constant (number or VariableEntity), then its derivative is 0, or a node, then there is a reference by name (InvokeDerive refers to the dictionary of functions, where the desired one is located (for example, the sum or sine)).

这是实体方法。 如我们所见，叶子只有两个状态：要么是我们用来区分的变量，然后其导数是1，要么是常数(数字或VariableEntity)，然后它的导数是0，或者是一个节点，然后有是按名称的引用(InvokeDerive是指功能字典，所需的功能位于该字典(例如，总和或正弦))。

Notice that I do not leave something like dy/dx here but claim that the derivative of the variable

请注意，我在这里没有留下dy / dx之类的东西，而是声称变量的导数

不 (not)

by which we differentiate is 0. But

以此来区分为0。但是

here it is done differently. 在这里，它是不同的。

All differentiation is described in a single file.

所有区别都在一个文件中描述。

表达式的简化。 模式 ( Simplification of an expression. Patterns )

Simplification of an expression in the general case is non-trivial. Well, for example, which expression is simpler:

or ? At this point, we stick to some ideas, and basing on them we want to make those rules so they could accurately simplify the expression.

通常情况下，简化表达式是不平凡的。 好吧，例如，哪个表达式更简单：

要么 ？ 在这一点上，我们坚持一些想法，并根据这些想法制定这些规则，以便它们可以准确地简化表达。

It is possible to write at every Eval that if we have the sum node, and its children are product nodes, then we will sort out four options, and if something is equal something else, we will take out the factor… But of course I do not want to do that. Therefore, we will use a system of rules and patterns. So what do we want? Something like this syntax:

可以在每个Eval处写道，如果我们有求和节点，而其子节点是乘积节点，那么我们将梳理出四个选择，而如果其他条件相等，我们将剔除该因子……但是我当然不想那样做。 因此，我们将使用规则和模式系统。 那我们想要什么？ 像这样的语法：

{ any1 / (any2 / any3)   ->   any1 * any3 / any2 },
{ const1 * var1 + const2 * var1   ->   (const1 + const2) * var1 },
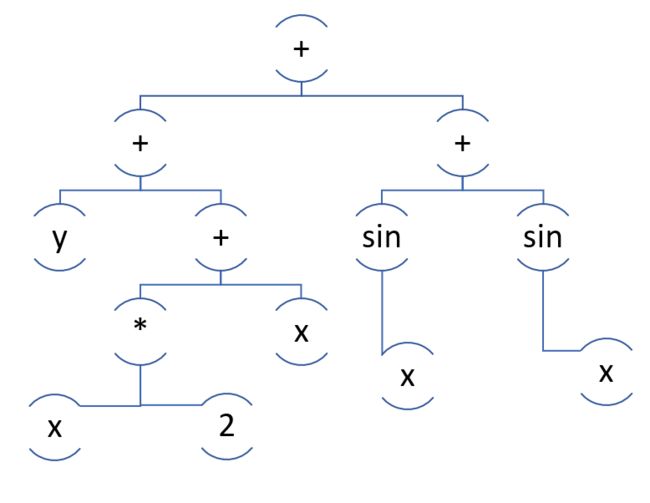
{ any1 + any1 * any2   ->   any1 * (Num(1) + any2) },

Here is an example of a tree in which a subtree was found (circled in green) that matches the pattern any1 + const1 * any1 (any1 found is circled in orange).

这是一棵树的示例，其中找到与模式any1 + const1 * any1(找到的any1用橙色圈出)匹配的子树(用绿色圈出)。

As you can see, sometimes it is important for us that one and the same entity must be repeated, for example, to reduce the expression

, we need to be both factor of the first and second monomial, because

is no longer reduceable. Therefore, we need to make an algorithm that not only checks that the tree matches the pattern, but also

如您所见，有时候对我们来说重要的是必须重复一个和一个相同的实体，例如，以减少 ， 我们需要

都是第一和第二多项式的因子，因为 不再是可减少的。 因此，我们需要制定一种算法，不仅要检查树是否与模式匹配，还要检查

1. Verify that the same Entity patterns match the same Entity.
   验证相同的实体模式是否与相同的实体匹配。
2. Gathers list of entites matching each pattern entity
   收集与每个模式实体匹配的实体列表

The entry point looks something like this:

入口点看起来像这样：

internal Dictionary EqFits(Entity tree)
{
    var res = new Dictionary();
    if (!tree.PatternMakeMatch(this, res))
        return null;
    else
        return res;
}

In tree.PaternMakeMatch, we recursively add keys and their values to the dictionary. Here is an example of a list of the Entity pattern itself:

在tree.PaternMakeMatch中，我们以递归方式将键及其值添加到字典中。 这是一个实体模式本身列表的示例：

static readonly Pattern any1 = new Pattern(100, PatType.COMMON);        
static readonly Pattern any2 = new Pattern(101, PatType.COMMON);
static readonly Pattern const1 = new Pattern(200, PatType.NUMBER);
static readonly Pattern const2 = new Pattern(201, PatType.NUMBER);
static readonly Pattern func1 = new Pattern(400, PatType.FUNCTION);

When we write any1 * const1 — func1 and so on, each node will have a number — this is the key. In other words, when filling out the dictionary, these numbers will appear as keys: 100, 101, 200, 201, 400… And when building a tree, we will look at the value corresponding to the key and substitute it.

当我们编写any1 * const1 — func1等时，每个节点都会有一个数字—这就是关键。 换句话说，当填写字典时，这些数字将作为键出现：100、101、200、201、400…。当构建一棵树时，我们将查看与键相对应的值并将其替换。

Implemented here.

在这里实施。

简化。 树排序 ( Simplification. Tree Sort )

In the article, to which I have already referred, the author decided to make it simple, and sorted it practically by the hash of the tree. He managed to reduce

and ,

to turn . But we, of course, also want

to be reduced, and in general more complicated things.

在我已经提到的文章中 ，作者决定简化它，并根据树的哈希对其进行排序。 他设法减少 和

， 转

。 但是我们当然也想要 减少，一般来说比较复杂。

这些模式不适合吗？ (Will the patterns not work for that? )

In general, patterns, that we used before, are a monstrously wonderful thing. It will allow you to reduce expressions like

, and Pythagorean trigonometric identity, and other complex things. But the elementary palm, , it will not reduce, because the main rule here is the commutativity of the terms. Therefore, the first step is to extract the «linear children.»

总的来说，我们以前使用的模式是一件非常了不起的事情。 它将使您减少诸如

，以及勾股三角的恒等式，以及其他复杂的事物。 但是基本的手掌 ，它不会减少，因为此处的主要规则是术语的可交换性。 因此，第一步是提取“线性子代”。

线性儿童 (Linear children)

Actually for each node of the sum or difference (and, by the way, the product/division), we want to get a list of terms (factors).

实际上，对于总和或差的每个节点(顺便说一下，乘积/除法)，我们希望获得一个术语(因子)列表。

This is basically straightforward. Let the LinearChildren(Entity node) function return a list, then we look at a child in node.Children: if child is not a sum, then result.Add (child), otherwise — result.AddRange (LinearChildren (child)).

这基本上很简单。 让LinearChildren(Entity node)函数返回一个列表，然后我们看一下node.Children中的一个孩子：如果child不是一个和，则为result.Add(孩子)，否则为result.AddRange(LinearChildren(孩子))。

Implemented not in the best way here.

此处未以最佳方式实施。

分组儿童 (Grouping children)

So we have a list of children, but what's next? Suppose we have

. Obviously, our algorithm will receive five terms. Next, we want to group by similarity, for example, looks like

more than .

因此，我们有一个孩子列表，但是接下来呢？ 假设我们有

。 显然，我们的算法将获得五个条件。 接下来，我们要按相似性分组，例如， 好像

多于 。

Here is a good grouping:

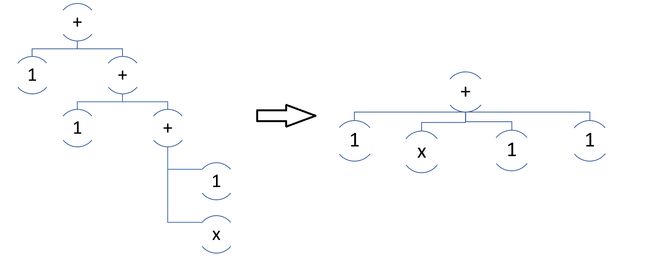
这是一个很好的分组：

Since the patterns in it will cope further with the conversion of

to .

由于其中的模式将进一步解决

至 。

That is, we first group by some hash, and then do MultiHang — converting n-ary summation to binary.

也就是说，我们首先按哈希进行分组，然后进行MultiHang －将n元求和转换为二进制。

节点哈希 (Node Hash)

On the one hand,

and should be placed in one group. On the other hand, in the presence of

, placing in the same group with is pointless.

一方面，

和 应该放在一组。 另一方面，在

，与 是没有意义的。

思想 (Thoughts)

Therefore, we implement multi-level sorting. First, we pretend that

and to be the same. Then we pretend that

can be placed only with other ,

etc. Finally, is only compatible with

. And now our and

finally merged. Implemented quite simply:

因此，我们实现了多级排序。 首先，我们假装 和

一样。 然后我们假装 只能与其他

， 等等，最后，

仅与 。 现在我们的

和 终于合并了。 实现起来非常简单：

internal string Hash(SortLevel level)
{
    if (this is FunctionEntity)
        return this.Name + "_" + string.Join("_", from child in Children select child.Hash(level));
    else if (this is NumberEntity)
        return level == SortLevel.HIGH_LEVEL ? "" : this.Name + " ";
    else if (this is VariableEntity)
        return "v_" + Name;
    else
        return (level == SortLevel.LOW_LEVEL ? this.Name + "_" : "") + string.Join("_", from child in Children where child.Hash(level) != "" select child.Hash(level));
}

As you can see, the function entity affects sorting in any way (of course, because

with is cannot be somehow reduced). Likewise, we cannot reduce

with . But the constants and operators are taken into account at some levels (but not all). That is how it is performed

如您所见，函数实体以任何方式影响排序(当然，因为

与 不能以某种方式减少)。 同样，我们不能减少

与 。 但是在某些级别(但不是全部)考虑了常量和运算符。 那就是它的执行方式

public Entity Simplify(int level)
{
    // First, we make the easiest simplification: calculating values where possible, multiplying by zero, etc.
    var stage1 = this.InnerSimplify();
    Entity res = stage1;
    for (int i = 0; i < level; i++)
    {
        // This block is responsible for sorting. First we group something like x and x + 1 (variables and functions), then something like x-1 and x + 1 (variables, functions and constants), then something like x + 1 and x + 1 (everything is taken into account).
        switch (i)
        {
            case 0: res = res.Sort(SortLevel.HIGH_LEVEL); break;
            case 2: res = res.Sort(SortLevel.MIDDLE_LEVEL); break;
            case 4: res = res.Sort(SortLevel.LOW_LEVEL); break;
        }
        // Here we replace the patterns.
        res = TreeAnalyzer.Replace(Patterns.CommonRules, res).InnerSimplify();
    }
    return res;
}

思想 (Thoughts)

I sort the tree here.

我在这里把树整理好。

功能的《汇编》 («Compilation» of functions)

In quotation marks — since it is not in the IL code itself, but only in a very fast set of instructions. But it is very simple.

用引号引起来-因为它不在IL代码本身中，而是仅在非常快速的一组指令中。 但这很简单。

替代问题 (Substitution Problem)

To calculate the value of a function, we just need to call the variable substitution and eval, for example

要计算一个函数的值，我们只需要调用变量替换和eval，例如

var x = MathS.Var("x");
var expr = x * x + 3;
var result = expr.Substitute(x, 5).Eval();

But it works slowly, about 1.5 microseconds per sine.

但是它工作缓慢，每个正弦大约1.5微秒。

使用说明 ( Instructions )

To speed up the calculation, we do a function calculation on the stack, namely:

为了加快计算速度，我们在堆栈上进行了函数计算，即：

1) We come up with the FastExpression class, which will have a list of instructions

1)我们提出了FastExpression类，该类将具有指令列表

2) When compiling, the instructions are stacked in the reverse order, that is, if there is a function

, then the instructions will be something like this:

2)编译时，指令以相反的顺序堆叠，即如果有函数 ，那么说明将如下所示：

PUSHVAR 0 // Variable Substitution Number 0 - x
CALL 6 // Call function №6 - sine
PUSHCONST 3
CALL 0 // Call function №0 - sum
PUSHVAR 0
PUSHVAR 0
CALL 2
CALL 0

Next, when invoked, we run these instructions and return a Number.

接下来，当被调用时，我们运行这些指令并返回一个数字。

An example of executing a sum statement:

执行sum语句的示例：

internal static void Sumf(Stack stack)
{
    Number n1 = stack.Pop();
    Number n2 = stack.Pop();
    stack.Push(n1 + n2);
}

The sine call time was reduced from 1500ns to 60ns (system Complex.Sin takes 30ns).

正弦调用时间从1500ns减少到60ns(系统Complex.Sin需要30ns)。

It is implemented here.

它在这里实现。

快取 (Cache)

There is still «room for improvement.» Let some function be

仍有“改进的空间。” 让一些功能成为

According to benchmarks, its performance (time/iteration) (i7-7700hq) is the following:

根据基准，其性能(时间/迭代)(i7-7700hq)如下：

Method	Time (nanoseconds)
Substitute	6800
Our compiled function	650
The same function written directly in code	430

方法	时间(纳秒)
替代	6800
我们的编译函数	650
直接用代码编写的相同功能	430

什么？ (What?)

var x = MathS.Var("x");
var expr = x + 3 * x;
Console.WriteLine(expr.Substitute(x, 5).Eval());
>>> 20

Our compiled function is when we do the same, but after compiling it

我们的编译函数是在执行相同的操作之后，但是在编译之后

var x = MathS.Var("x");
var expr = x + 3 * x;
var func = expr.Compile(x);
Console.WriteLine(func.Substitute(5));

A function written directly in code is when we do

直接用代码编写的函数是

static Complex MyFunc(Complex x)
            => x + 3 * x;

As we can see, this function has repeating parts, for example,

, and it would be nice to cache them.

如我们所见，该函数具有重复部分，例如， ，最好将它们缓存起来。

To do this, we introduce two more instructions PULLCACHE and TOCACHE. The first one will push onto the stack the number in the cache at the address that we pass to it. The second will copy (stack.Peek()) the last number from the stack to the cache, also at a specific address.

为此，我们再介绍两个指令PULLCACHE和TOCACHE。 第一个将把高速缓存中我们传递给它的地址上的数字压入堆栈。 第二个也会将堆栈中的最后一个数字( stack.Peek() ) 复制到高速缓存中，同样位于特定地址。

It remains to make a table into which during compilation we will write functions for caching. What we will not cache? Well, firstly, what happens once. The extra instruction to access the cache is not good. Secondly, operations that are too simple also make no sense to cache, such as accessing a variable or number.

剩下的就是要创建一个表，在编译期间我们将在其中编写用于缓存的函数。 我们不会缓存什么？ 好吧，首先，一旦发生。 访问缓存的额外指令不好。 其次，过于简单的操作也无济于事，例如访问变量或数字。

When interpreting the list of instructions, we will have a pre-created array for caching. Now the instructions for this function look like

在解释指令列表时，我们将有一个预先创建的用于缓存的数组。 现在，此功能的说明如下

PUSHCONST (2, 0)
PUSHVAR 0
CALL powf
TOCACHE 0       #at this point we compute n^2, and since we need it more than once, we cache it.
CALL sinf
TOCACHE 1         #we will also need sin(n^2)
PULLCACHE 0      #when we encounter mention of a cached function, we pull the apporpriate element. 
PULLCACHE 0
CALL cosf
PULLCACHE 1
CALL sumf
CALL sumf
CALL sumf

Finally, we get a clearly better result:

最后，我们得到了明显更好的结果：

Method	Time (nanoseconds)
Substitute	6800
Our compiled functions	330 (previous result: 650)
The same function written directly in code	430

方法	时间(纳秒)
替代	6800
我们编译的函数	330 (先前的结果：650)
直接用代码编写的相同功能	430

Compilation and interpretation of instructed are located here.

指令的编辑和解释位于此处 。

胶乳 (LaTeX)

This is a well-known format for mathematical formulas (although not only them!), which is rendered into a more human-readable format. It is also used on Habr, and all the formulas that I write are just written in this format.

这是数学公式的一种众所周知的格式(尽管不仅如此！)，它被转换为更易于理解的格式。 它也用于Habr，我编写的所有公式都是以此格式编写的。

Having an expression tree makes rendering in latex very simple. How to do this in terms of logic? So, we have the top of the tree. If it is a number or a variable, then everything is simple. If this vertex, for example, is a division operator, we want

instead of (

and are the children of the vertex), so for division we write something like

拥有表达式树使在乳胶中渲染非常简单。 在逻辑上该怎么做？ 因此，我们拥有了树的顶部。 如果是数字或变量，则一切都很简单。 例如，如果此顶点是除法运算符，我们需要

代替 (

和 是顶点的子代)，所以对于除法，我们写类似

public static class Div
{
    internal static string Latex(List args)
    => @"\frac{" + args[0].Latexise() + "}{" + args[1].Latexise() + "}";
}

Everything is very simple, as we see. The only problem I encountered during the implementation is that it is not clear how to place braces. If we just wrap each operator with braces, we will get such nonsense:

正如我们所见，一切都非常简单。 我在实现过程中遇到的唯一问题是不清楚如何放置括号。 如果只用大括号括起来，就会得到这样的废话：

In contrast, if you completely remove them, then given an expression of the form

, we will print

相反，如果您完全删除了它们，则给出以下形式的表达式 ，我们将打印

It is resolved simply, we enter the priorities of the operators like

简单地解决，我们输入像

args[0].Latexise(args[0].Priority < Const.PRIOR_MUL) + "*" + args[1].Latexise(args[1].Priority < Const.PRIOR_MUL);

Latexisation is here. By the way, word «latexise» does not exist, I invented it myself.

乳胶化在这里 。 顺便说一句，“ latexise”一词不存在，我自己发明了。

解方程 (Solving Equations)

Actually, from the point of view of mathematics, you cannot write an algorithm that finds all the solutions of some equation. Therefore, we want to find as many different roots as possible, realizing the unattainability of the final goal. There are two components: a numerical solution (everything is as simple as possible) and analytical (that is the thing).

实际上，从数学的角度来看，您无法编写找到某个方程式所有解的算法。 因此，我们希望找到尽可能多的不同根源，以实现最终目标的不可实现性。 有两个部分：数值解(一切都尽可能简单)和解析性(就是这样)。

数值解。 牛顿法 ( Numerical solution. Newton's Method )

It is extremely simple, given the function

we will search for the root using the iterative formula

给定功能非常简单 我们将使用迭代公式搜索根

Since roots might be also located in a complex plane, we can basically write a two-dimensional loop that will look for solutions and then return unique ones. In this case, we can now find the derivative of the function analytically, and then compile both functions

and .

由于根也可能位于复杂平面中，因此我们基本上可以编写一个二维循环，该循环将寻找解，然后返回唯一的解。 在这种情况下，我们现在可以解析地找到函数的导数，然后编译两个函数

和 。

Newton's method is located here.

牛顿法在这里 。

分析溶液 (Analytical Solution)

First thoughts are pretty obvious. Clearly, the roots of equation

are equal to the set of roots and

, similarly for division:

最初的想法很明显。 显然，等式的根源 等于根的集合

和 ，对于除法类似：

internal static void Solve(Entity expr, VariableEntity x, EntitySet dst)
{
    if (expr is OperatorEntity)
    {
        switch (expr.Name)
        {
            case "mul":
                Solve(expr.Children[0], x, dst);
                Solve(expr.Children[1], x, dst);
                return;
            case "div":
                Solve(expr.Children[0], x, dst);
                return;
        }
    }
...

For sine, this will be realized a little different:

对于正弦，这将实现一些不同：

case "sinf":
    Solve(expr.Children[0] + "n" * MathS.pi, x, dst);
    return;

After all, we want to find all the roots, and not just those that are 0.

毕竟，我们要查找所有的根，而不仅仅是找到0的根。

After we have made sure that the current expression is not a product, and not other easily simplified operators and functions, we need to try to find a template for solving the equation.

在确保当前表达式不是乘积，也不是其他易于简化的运算符和函数之后，我们需要尝试找到用于求解方程的模板。

The first idea is to use the patterns we made to simplify the expression. And in fact, we will need approximately this, but first we need to do a variable replacement. And indeed, to the equation

第一个想法是使用我们制作的模式简化表达式。 实际上，我们大约需要这个，但是首先我们需要进行变量替换。 实际上，对于等式

there is no pattern, but to the pair

没有模式，但对

there is a pattern of a quadratic expression and arcsin.

有一个二次表达式和反正弦的模式。

Therefore, we are to develop a function «GetMinimumSubtree», which would return the most efficient variable replacement. What is an effective replacement? This is such a replacement in which we

因此，我们将开发一个函数“ GetMinimumSubtree”，该函数将返回最有效的变量替换。 什么是有效的替代品？ 这是我们的替代品

1. Maximize the use of this replacement

   最大限度地利用这种替代

2. Maximize the depth of the tree (so that in the equation we have the replacement )

   最大化树的深度(以便等式中 我们有替代品 )

3. We make sure that with this substitution we replaced

   我们确保通过这种替换我们替换了

   所有 (all)

   the mentions of the variable, for example, if in the equation

   变量的提及，例如，如果在等式中

   we make the replacement 我们进行更换 , then we will not be able to solve it. Therefore, in this equation, the best replacement for ，那么我们将无法解决它。 因此，在此等式中，最佳替代 is 是 (that is, there is no good replacement), but for example in (也就是说，没有好的替代品)，例如 we can safely do the replacement 我们可以安全地进行更换 . 。

After replacing the equation looks a lot simpler.

替换方程后，看起来要简单得多。

多项式 (Polynomial)

So, the first thing we do is expr.Expand() — open all the brackets to get rid of the muck of the form

, turning it into . Now, after the disclosure, we get something like

因此，我们要做的第一件事是expr.Expand() -打开所有括号以摆脱表格的内容

，将其变成 。 现在，在披露之后，我们得到类似

Not canonical? Then we first collect information about each monomial by applying “linear children” and expanding all the terms.

不规范吗？ 然后，我们首先通过应用“线性子代”并扩展所有术语来收集有关每个单项式的信息。

What do we have about the monomial? A monomial is a product of factors, one of which is a variable, or an operator of the degree of a variable and an integer. Therefore, we will introduce two variables, one will have a degree, and the other a coefficient. Next, we simply go through the factors, and each time we are convinced that either

is there to an integer degree, or without a degree at all. If we encounter something unexpected — we return with null.

我们对单项式有什么看法？ 单项式是因子的乘积，因子之一是变量，或者是变量和整数的次数的算符。 因此，我们将介绍两个变量，一个具有度，另一个具有系数。 接下来，我们简单地研究这些因素，每次我们确信 有一个整数度，或根本没有度。 如果遇到意外情况，则返回null。

h (Feh)

Okay, we have compiled a dictionary in which the key is a degree (of a polynomial) (integer) and the value is a monomial coefficient. This is what it looks like for the previous example:

好的，我们已经编译了一个字典，其中的键是(多项式的)度(整数)，值是一个单项系数。 这是上一个示例的样子：

0 => c
1 => 1
2 => 3
3 => 1 - a

That is how solving of the quadratic equation is implemented

这就是实现二次方程式的方法

if (powers[powers.Count - 1] == 2)
{
    var a = GetMonomialByPower(2);
    var b = GetMonomialByPower(1);
    var c = GetMonomialByPower(0);
    var D = MathS.Sqr(b) - 4 * a * c;
    res.Add((-b - MathS.Sqrt(D)) / (2 * a));
    res.Add((-b + MathS.Sqrt(D)) / (2 * a));
    return res;
}

This thing has not yet been completed, but in general this is here.

这件事尚未完成，但总的来说，这是这里 。

反向更换 (Reverse replacement)

So, here we have made some kind of replacement like

, and now we want to find from there. Here we just have a step-by-step deployment of functions and operators, such as

因此，在这里我们做了一些替代，例如

，现在我们想找到 从那里。 在这里，我们只是逐步部署功能和运算符，例如

The code snippet looks something like this:

该代码段如下所示：

switch (func.Name)
{
    case "sinf":
        // sin(x) = value => x = arcsin(value)
        return FindInvertExpression(a, MathS.Arcsin(value), x);
    case "cosf":
        // cos(x) = value => x = arccos(value)
        return FindInvertExpression(a, MathS.Arccos(value), x);
    case "tanf":
        // tan(x) = value => x = arctan(value)
        return FindInvertExpression(a, MathS.Arctan(value), x);
...

The code for these functions is here.

这些功能的代码在这里 。

Everything, the final solving algorithm of the equations (yet!) Looks something like this

一切，方程式的最终求解算法(至今！)看起来像这样

1. If we know the zero of the function or operator, send Solve there (for example, if , then run Solve(a) and Solve(b))

   如果我们知道函数或运算符的零，则在此处发送Solve(例如，如果 ，然后运行Solve(a)和Solve(b))

2. Find a replacement
   寻找替代品
3. Solve as a polynomial, if possible
   尽可能解决多项式
4. For all solutions, deploy a replacement to get the final solution
   对于所有解决方案，请部署替代产品以获得最终解决方案

5. If, as a polynomial, it did not resolve

   如果作为多项式，它没有解析

   和 ( and )

   we have only one variable, we solve it by Newton’s method

   我们只有一个变量，我们用牛顿法求解

That's it for now. Because this article is the translation of the two in Russian (first and second parts), it only contains features realized up to the moment of 9-th January. However, we implemented tons of new features and have something to tell. Soon, there will be the third part.

现在就这样。 由于本文是俄语和俄语两个版本的翻译( 第一部分和第二部分)，因此仅包含直到1月9日为止的功能。 但是，我们实现了许多新功能，并且有话要说。 很快，将有第三部分。

There are also a couple of examples of how the project works:

还有一些有关该项目如何工作的示例：

var x = MathS.Var("x");
var y = MathS.Var("y");
var c = x * y + x / y;
Console.WriteLine(MathS.Sqr(c));
>>> (x * y + x / y) ^ 2

var x = MathS.Var("x");
var expr = x * 2 + MathS.Sin(x) / MathS.Sin(MathS.Pow(2, x));
var subs = expr.Substitute(x, 0.3);
Console.WriteLine(subs.Eval());
>>> 0,9134260185941638

var x = MathS.Var("x");
var func = MathS.Sqr(x) + MathS.Ln(MathS.Cos(x) + 3) + 4 * x;
var derivative = func.Derive(x);
Console.WriteLine(derivative.Eval());
>>> 2 * x + -1 * sin(x) / (cos(x) + 3) + 4

var x = MathS.Var("x");
var a = MathS.Var("a");
var b = MathS.Var("b");
var expr = MathS.Sqrt(x) / x + a * b + b * a + (b - x) * (x + b) + 
    MathS.Arcsin(x + a) + MathS.Arccos(a + x);
Console.WriteLine(expr.Simplify());
>>> 1.5707963267948966 + 2 * a * b + b ^ 2 + x ^ (-0.5) - x ^ 2

var x = MathS.Var("x");
var y = MathS.Var("y");
var expr = x.Pow(y) + MathS.Sqrt(x + y / 4) * (6 / x);
Console.WriteLine(expr.Latexise());
>>> {x}^{y}+\sqrt{x+\frac{y}{4}}*\frac{6}{x}

var x = MathS.Var("x");
var expr = MathS.Sin(x) + MathS.Sqrt(x) / (MathS.Sqrt(x) + MathS.Cos(x)) + MathS.Pow(x, 3);
var func = expr.Compile(x);
Console.WriteLine(func.Substitute(3));
>>> 29.4752368584034

Entity expr = "(sin(x)2 - sin(x) + a)(b - x)((-3) * x + 2 + 3 * x ^ 2 + (x + (-3)) * x ^ 3)";
foreach (var root in expr.Solve("x"))
    Console.WriteLine(root);
>>> arcsin((1 - sqrt(1 + (-4) * a)) / 2)
>>> arcsin((1 + sqrt(1 + (-4) * a)) / 2)
>>> b
>>> 1
>>> 2
>>> i
>>> -i

Thanks for your attention!

感谢您的关注！

翻译自: https://habr.com/en/post/486496/

c#解微分方程