协同过滤
一、协同过滤算法
协同过滤推荐分为三种类型。
- 第一种是基于用户(user-based)的协同过滤:给用户推荐和他兴趣相似的其他用户喜欢的产品;
- 第二种是基于物品(item-based)的协同过滤:给用户推荐和他之前喜欢的物品相似的物品。
- 第三种是基于模型(model based)的协同过滤:用机器学习的思想来建模,利用已有的部分稀疏数据来预测那些空白的物品和数据之间的评分关系,找到最高评分的物品推荐给用户。
二、相似性度量方法
1.杰卡德(Jaccard)相似系数
- 杰卡德(Jaccard)相似系数用符号 s i m u v sim_{uv} simuv表示,其中 N ( u ) , N ( v ) N(u),N(v) N(u),N(v)分别表示用户 u u u和用户 v v v交互商品的集合。
s i m u v = ∣ N ( u ) ∩ N ( v ) ∣ ∣ N ( u ) ∣ ∪ ∣ N ( v ) ∣ sim_{uv}=\frac{|N(u) \cap N(v)|}{\sqrt{|N(u)| \cup|N(v)|}} simuv=∣N(u)∣∪∣N(v)∣∣N(u)∩N(v)∣ - 作用:由于杰卡德相似系数一般无法反映具体用户的评分喜好信息, 所以常用来评估用户是否会对某商品进行打分, 而不是预估用户会对某商品打多少分。
2.余弦相似度
- 公式:
s i m u v = c o s ( u , v ) = u ⋅ v ∣ u ∣ ⋅ ∣ v ∣ sim_{uv} = cos(u,v) =\frac{u\cdot v}{|u|\cdot |v|} simuv=cos(u,v)=∣u∣⋅∣v∣u⋅v - 实现:
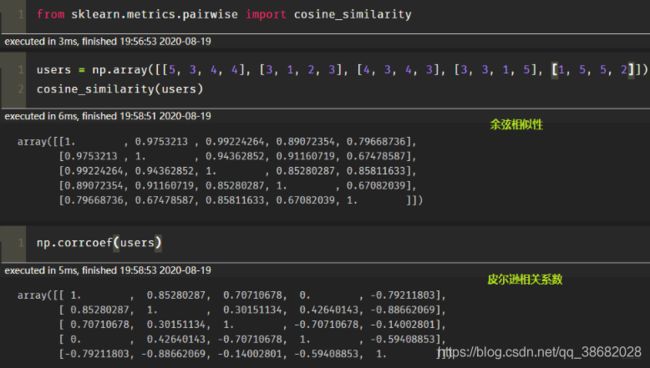
from sklearn.metrics.pairwise import cosine_similarity
a = [1, 0, 0, 0]
b = [1, 0.5, 0.5, 0]
cosine_similarity([a, b])
3.皮尔逊相关系数
- s i m ( u , v ) = ∑ i ∈ I ( r u i − r ˉ u ) ( r v i − r ˉ v ) ∑ i ∈ I ( r u i − r ˉ u ) 2 ∑ i ∈ I ( r v i − r ˉ v ) 2 sim(u,v)=\frac{\sum_{i\in I}(r_{ui}-\bar r_u)(r_{vi}-\bar r_v)}{\sqrt{\sum_{i\in I }(r_{ui}-\bar r_u)^2}\sqrt{\sum_{i\in I }(r_{vi}-\bar r_v)^2}} sim(u,v)=∑i∈I(rui−rˉu)2∑i∈I(rvi−rˉv)2∑i∈I(rui−rˉu)(rvi−rˉv)
其中 r u i , r v i r_{ui},r_{vi} rui,rvi分别表示用户 u u u和用户 v v v对商品 i i i是否有交互(或者具体的评分值), r ˉ u , r ˉ v \bar r_u, \bar r_v rˉu,rˉv分别表示用户 u u u和用户 v v v交互的所有商品交互数量或者具体评分的平均值。 - 相比余弦相似度,皮尔逊相关系数通过使用用户的平均分对各独立评分进行修正,减小了用户评分偏置的影响。
- 实现
from scipy.stats import pearsonr
i = [1, 0, 0, 0]
j = [1, 0.5, 0.5, 0]
pearsonr(i, j)
三、基于用户的协同过滤(UserCF)
基于用户的协同过滤,简要来说就是臭味相投。判断“用户”相似主要通过对用户过去的行为轨迹进行计算而得。
1.算法步骤
- 找到和目标用户兴趣相似的集合;
- 找到这个集合中的用户喜欢的, 且目标用户没有听说过的物品推荐给目标用户。
2.计算实例
两个步骤:
- 1)首先根据前面的这些打分情况(或者说已有的用户向量)计算一下Alice和用户1, 2, 3, 4的相似程度, 找出与Alice最相似的n个用户
- 2)根据这n个用户对物品5的评分情况和与Alice的相似程度会猜测出Alice对物品5的评分, 如果评分比较高的话, 就把物品5推荐给用户Alice, 否则不推荐。
第一个步骤,可由上面的相似性计算方法而得。
最终结果的预测
A. 常用的方式之一是利用用户相似度和相似用户的评价加权平均获得用户的评价预测, 用下面式子表示:
R u , p = ∑ s ∈ S ( w u , s ⋅ R s , p ) ∑ s ∈ S w u , s R_{\mathrm{u}, \mathrm{p}}=\frac{\sum_{\mathrm{s} \in S}\left(w_{\mathrm{u}, \mathrm{s}} \cdot R_{\mathrm{s}, \mathrm{p}}\right)}{\sum_{\mathrm{s} \in S} w_{\mathrm{u}, \mathrm{s}}} Ru,p=∑s∈Swu,s∑s∈S(wu,s⋅Rs,p)
权重 w u , s w_{u,s} wu,s是用户 u u u和用户 s s s的相似度, R s , p R_{s,p} Rs,p是用户 s s s对物品 p p p的评分。
B. 不单纯的是其他用户对物品的评分, 而是该物品的评分与此用户的所有评分的差值进行加权平均, 这时候考虑到了有的用户内心的评分标准不一的情况, 即有的用户喜欢打高分, 有的用户喜欢打低分的情况。
P i , j = R ˉ i + ∑ k = 1 n ( S i , k ( R k , j − R ˉ k ) ) ∑ k = 1 n S j , k P_{i, j}=\bar{R}{i}+\frac{\sum{k=1}^{n}\left(S_{i, k}\left(R_{k, j}-\bar{R}{k}\right)\right)}{\sum{k=1}^{n} S_{j, k}} Pi,j=Rˉi+∑k=1nSj,k∑k=1n(Si,k(Rk,j−Rˉk))
详细计算如下:
- 根据相似度用户计算Alice对物品5的最终得分
用户1对物品5的评分是3, 用户2对物品5的打分是5, 那么根据上面的计算公式, 可以计算出Alice对物品5的最终得分是: P A l i c e , 物 品 5 = R ˉ A l i c e + ∑ k = 1 2 ( S A l i c e , u s e r k ( R u s e r k , 物 品 5 − R ˉ u s e r k ) ) ∑ k = 1 2 S A l i c e , u s e r k = 4 + 0.85 ∗ ( 3 − 2.4 ) + 0.7 ∗ ( 5 − 3.8 ) 0.85 + 0.7 = 4.87 P_{Alice, 物品5}=\bar{R}{Alice}+\frac{\sum{k=1}^{2}\left(S_{Alice,user k}\left(R_{userk, 物品5}-\bar{R}{userk}\right)\right)}{\sum{k=1}^{2} S_{Alice, userk}}=4+\frac{0.85*(3-2.4)+0.7*(5-3.8)}{0.85+0.7}=4.87 PAlice,物品5=RˉAlice+∑k=12SAlice,userk∑k=12(SAlice,userk(Ruserk,物品5−Rˉuserk))=4+0.85+0.70.85∗(3−2.4)+0.7∗(5−3.8)=4.87 - 根据用户评分对用户进行推荐
这时候, 我们就得到了Alice对物品5的得分是4.87, 根据Alice的打分对物品排个序从大到小: 物 品 1 > 物 品 5 > 物 品 3 = 物 品 4 > 物 品 2 物品1>物品5>物品3=物品4>物品2 物品1>物品5>物品3=物品4>物品2 这时候,如果要向Alice推荐2款产品的话, 我们就可以推荐物品1和物品5给Alice。
四、基于物品的协同过滤
1.算法步骤
- 计算物品之间的相似度
- 根据物品的相似度和用户的历史行为给用户生成推荐列表(购买了该商品的用户也经常购买的其他商品)
2.计算实例
1)实际计算步骤:
数据如图1所示。
- 首先计算一下物品5和物品1, 2, 3, 4之间的相似性(它们也是向量的形式, 每一列的值就是它们的向量表示, 因为ItemCF认为物品a和物品c具有很大的相似度是因为喜欢物品a的用户大都喜欢物品c, 所以就可以基于每个用户对该物品的打分或者说喜欢程度来向量化物品)
- 找出与物品5最相近的n个物品
- 根据Alice对最相近的n个物品的打分去计算对物品5的打分情况
2)具体计算:
计算如图5所示:

根据皮尔逊相关系数, 可以找到与物品5最相似的2个物品是item1和item4(n=2), 下面基于上面的公式计算最终得分:
P A l i c e , 物 品 5 = R ˉ 物 品 5 + ∑ k = 1 2 ( S 物 品 5 , 物 品 k ( R A l i c e , 物 品 k − R ˉ 物 品 k ) ) ∑ k = 1 2 S 物 品 k , 物 品 5 = 13 4 + 0.97 ∗ ( 5 − 3.2 ) + 0.58 ∗ ( 4 − 3.4 ) 0.97 + 0.58 = 4.6 P_{Alice, 物品5}=\bar{R}{物品5}+\frac{\sum{k=1}^{2}\left(S_{物品5,物品 k}\left(R_{Alice, 物品k}-\bar{R}{物品k}\right)\right)}{\sum{k=1}^{2} S_{物品k, 物品5}}=\frac{13}{4}+\frac{0.97*(5-3.2)+0.58*(4-3.4)}{0.97+0.58}=4.6 PAlice,物品5=Rˉ物品5+∑k=12S物品k,物品5∑k=12(S物品5,物品k(RAlice,物品k−Rˉ物品k))=413+0.97+0.580.97∗(5−3.2)+0.58∗(4−3.4)=4.6
五、基于模型的协同过滤(Model-based Collaborative Filtering)
- 用关联算法做协同过滤
如果用户购买了频繁N项集或者序列里的部分物品,那么我们可以将频繁项集或序列里的其他物品按一定的评分准则推荐给用户,这个评分准则可以包括支持度,置信度和提升度等。
常用的关联推荐算法有Apriori,FP Tree和PrefixSpan。 - 用聚类算法做协同过滤
- 按照用户或者按照物品基于一定的距离度量来进行聚类。
- 常用的聚类推荐算法有K-Means, BIRCH, DBSCAN和谱聚类。
- 用分类算法做协同过滤
如果我们根据用户评分的高低,将分数分成几段的话,则这个问题变成分类问题。常见的分类推荐算法有逻辑回归和朴素贝叶斯,两者的特点是解释性很强。 - 用回归算法做协同过滤
用回归算法做协同过滤比分类算法看起来更加的自然。我们的评分可以是一个连续的值而不是离散的值, 通过回归模型我们可以得到目标用户对某商品的预测打分。
常用的回归推荐算法有Ridge回归,回归树和支持向量回归。 - 用矩阵分解做协同过滤
目前主流的矩阵分解推荐算法主要是SVD的一些变种,比如FunkSVD,BiasSVD和SVD++。 - 用神经网络做协同过滤
用神经网络乃至深度学习做协同过滤应该是以后的一个趋势。目前比较主流的用两层神经网络来做推荐算法的是限制玻尔兹曼机(RBM)。 - 用图模型做协同过滤
用图模型做协同过滤,则将用户之间的相似度放到了一个图模型里面去考虑,常用的算法是SimRank系列算法和马尔科夫模型算法。 - 用隐语义模型做协同过滤
隐语义模型主要是基于NLP的,涉及到对用户行为的语义分析来做评分推荐,主要方法有隐性语义分析LSA和隐含狄利克雷分布LDA。
参考:
1.协同过滤
2.人工智能推荐算法(一) - 协同过滤算法介绍