python数据分析与挖掘实战——协同过滤——关联算法——Apriori算法菜品推荐

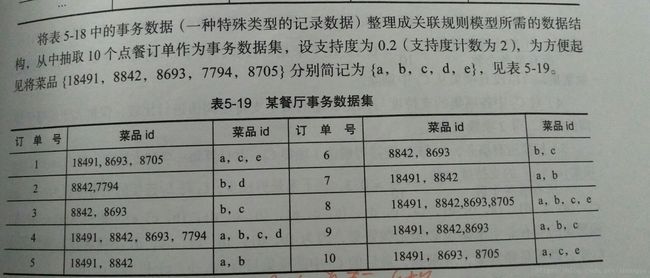
客户在餐厅点餐时，面对着菜单中大量的菜品信息，往往无法迅速的找到满意的菜品，既增加了点菜的时间，也降低了客户的就餐体验。实际上，菜品的合理搭配是有规律可循的：顾客的饮食习惯，菜品的荤素和口味，有些菜品之间是互相关联的，而有些菜品之间是对立或竞争关系（负关联）。这些规律都隐藏在大量的历史菜单数据中，如果能够通过数据挖掘发现客户点餐的规律，就可以快速识别客户的口味，当他下了某个菜品的订单时推荐相关联的菜品，引导客户消费，提高顾客的就餐体验和餐饮企业的业绩水平。

Apriori的核心思想就是通过连接产生候选项以及支持度，然后通过剪枝生成频繁项集。

关联规则与频繁项集

（1）关联规则的一般形式

项集A、B同时发生的概率称为关联规则的支持度（也称为相对支持度）

support(a=>b) = P(a|b)

项集a发生，则项集b发生的概率为关联规则的置信度

confidence（a=>b）= P(b|a)

(2)最小支持度和最小置信度

最小支持度是用户或专家的衡量支持度的一个阈值，表示项目集在统计意义上的最低重要性，最小置信度是用户或专家定义的衡量置信度的一个阈值，表示关联规则的最低可靠性。同时满足最小支持度和最小置信度阈值的规则称为强规则。

（3）项集

项集是项的集合。包含K个项的项集称为k项集，如{牛奶、麦片、糖}是一个三项集。

项集出现的频率是所有包含项集的事务计数，又称作绝对支持度或支持度计数。如果项集I的相对支持度满足预定义的最小支持度阈值，则I是频繁项集，频繁k项集通常称为k

（4）支持度计数

项集A的支持度计数是事务数据集中包含项集A 的事务个数，简称为项集的频率或计数。

已知项集的支持度计数，则规则A=>B的支持度和置信度很容易从所有事务计数、项集A和项集B和项集A∪B的支持度推出。

Support(A=>B) = A,B同时发生的事务个数 / 所有事务个数 = support_count(A∩B）/ Support_count(A)

confidence(A=>B)  = P(A|B) =  support(A∩B）/ Support(A)= support_count(A∩B）/ Support_count(A)

 

书上给出的Apriori实现的代码

from __future__ import print_function
import pandas as pd

#自定义连接函数，用于实现L_{k-1}到C_k的连接 
#x是输入的数据，ms是连接的符号
def connect_string(x, ms):
  #这里是扫描所有的事物，一项频繁集L1与L1连接得到候选的2项集C2，并计算每一项的支持度。
  #然后与最小支持度阈值比较，得到2项频繁集L2
  '''
  在处理之前输出了一下数据
  # print('x',x)
  # x['a', 'c', 'e', 'b']
  x['a---c', 'a---e', 'a---b', 'c---e', 'b---c']
  x['a---c---e', 'a---b---c']
  '''
  x = list(map(lambda i:sorted(i.split(ms)), x))
  '''
  #分割处理后输出了一下数据
  # print('x',x)
  # x[['a'], ['c'], ['e'], ['b']]
  x [['a', 'c'], ['a', 'e'], ['a', 'b'], ['c', 'e'], ['b', 'c']]
  x [['a', 'c', 'e'], ['a', 'b', 'c']]
  '''
  l = len(x[0])
  r = []
  #一项频繁集L1与L1连接得到候选的2项集C2
  for i in range(len(x)):
    for j in range(i,len(x)):
      if x[i][:l-1] == x[j][:l-1] and x[i][l-1] != x[j][l-1]:
        r.append(x[i][:l-1]+sorted([x[j][l-1],x[i][l-1]]))
  return r

#寻找关联规则的函数
def find_rule(d, support, confidence, ms = u'--'):
  #这一步简单定义了要输出的格式
  result = pd.DataFrame(index=['support', 'confidence']) #定义输出结果
  # #项集的支持度，也就是说事物中包含项集{xx}的个数，比如，餐厅的订单事务集中，
  # #包含a的有7个
  # print('d.sum', d.sum())
  # # 所有事物的个数，这里的事物值得是数据集的大小
  # print('len(d)',len(d))
  support_series = 1.0*d.sum()/len(d)
  # #各个项集支持度序列
  # print('support_series',support_series)
  #初步根据支持度筛选,对初步得到的各项集的支持度与事先指定的最小支持度阈值进行比较，
  #保留大于或等于该阈值的项，得一项频繁集
  column = list(support_series[support_series > support].index)
  #print('column',column)
  k = 0

  while len(column) > 1:
    k = k+1
    print(u'\n正在进行第%s次搜索...' %k)
    #ms是连接的符号，column是第一步得到的频繁项集
    column = connect_string(column, ms)
    '''
    # print('column',column)
    # column[['a', 'c'], ['a', 'e'], ['a', 'b'], ['c', 'e'], ['b', 'c'], ['b', 'e']]
    column [['a', 'c', 'e'], ['a', 'b', 'c'], ['a', 'b', 'e']]
    column []
    '''
    print(u'数目：%s...' %len(column))
    sf = lambda i: d[i].prod(axis=1, numeric_only = True) #新一批支持度的计算函数

    #创建连接数据，这一步耗时、耗内存最严重。当数据集较大时，可以考虑并行运算优化。
    #print(map(sf,column))
    d_2 = pd.DataFrame(list(map(sf,column)), index = [ms.join(i) for i in column]).T
    #print('d2',d_2)
    support_series_2 = 1.0*d_2[[ms.join(i) for i in column]].sum()/len(d) #计算连接后的支持度
    column = list(support_series_2[support_series_2 > support].index) #新一轮支持度筛选
    support_series = support_series.append(support_series_2)
    column2 = []

    for i in column: #遍历可能的推理，如{A,B,C}究竟是A+B-->C还是B+C-->A还是C+A-->B？
      i = i.split(ms)
      #print(i)
      for j in range(len(i)):
        column2.append(i[:j]+i[j+1:]+i[j:j+1])
    print(column2)


    cofidence_series = pd.Series(index=[ms.join(i) for i in column2]) #定义置信度序列

    for i in column2: #计算置信度序列
      cofidence_series[ms.join(i)] = support_series[ms.join(sorted(i))]/support_series[ms.join(i[:len(i)-1])]

    for i in cofidence_series[cofidence_series > confidence].index: #置信度筛选
      result[i] = 0.0
      result[i]['confidence'] = cofidence_series[i]
      result[i]['support'] = support_series[ms.join(sorted(i.split(ms)))]

  result = result.T.sort_values (['confidence','support'], ascending = False) #结果整理，输出
  print(u'\n结果为：')
  print(result)

  return result

apriori算法的主要思想就是找出存在于事务数据集中的最大频繁项集，再利用最大的频繁项集与预先设定的最小置信度阈值生成强关联规则。

（1）apriori的性质

频繁项集的所有非空子集一定也是频繁项集

（2）apriori实现的两个过程

1)找出所有的频繁项集（支持度必须大于等于给定的最小支持度阈值），在这个过程中连接步和剪枝步互相融合，最终得到最大频繁项集Lk

连接步：

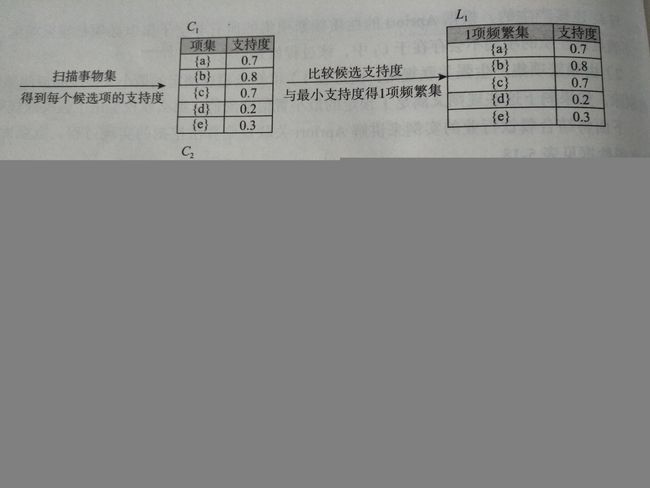
连接步的目的是找到K项集。对给定的最小支持度阈值，分别对1项候选集C1，剔除小于该阈值的项集得到1项频繁集L1，下一步由L1自身连接产生2项候选集C2，保留C2中满足约束条件的项集得到2项频繁集，记为L2，再下一步由L2与L1连接产生3项候选集C3，保留C2中满足约束条件的项集得到3项频繁集记为L3.。。。这样循环下去，得到频繁项集Lk

剪枝步：

剪枝步紧接着连接步，在产生候选项Ck的过程中起到减小搜索空间的目的。由于Ck是Lk-1 与 L1连接产生的，根据apriori的性质频繁项集的所有非空子集也必须是频繁项集，所以不满足该性质的项集不会存在于CK中，过程就是剪枝。

2）由频繁项集产生强关联规则，由以上过程可知未超过预定的最小支持度阈值的项集已经被剔除，如果剩下的这些规则又满足了预定的最小置信度阈值，那么就挖掘出了强关联规则。

 

#使用apriori算法挖掘菜品订单关联规则
import pandas as pd
from apriori import *#导入自行编写的apriori函数
inputfile = 'file/menu_orders.xls'
outputfile = 'outputfiel/save.xls'
data = pd.read_excel(inputfile,header=None)
print('转换原始数据至0-1矩阵')
#转换0-1矩阵的过度函数
ct = lambda x:pd.Series(1,index=x[pd.notnull(x)])
b = map(ct,data.as_matrix())#用map方式执行
#实现矩阵转换，缺失值用0填充
data = pd.DataFrame(list(b)).fillna(0)
print(u'\n转换完毕')
del b
support = 0.2
confidence = 0.5
ms = '---'#连接符，用来区分不同元素，默认‘--’，
find_rule(data,support,confidence,ms).to_excel(outputfile)#保存结果

就第一条输出结果进行解释：客户同时点菜品e和a的概率是30%。点了菜品e,再点菜品a的概率是100%。知道了这些，就可以对顾客进行智能推荐，增加销量同时满足客户需求