UNIRE: A Unified Label Space for Entity Relation Extraction

UNIRE: A Unified Label Space for Entity Relation Extraction

UNIRE：一种用于实体关系抽取的统一标签空间

https://github.com/Receiling/UniRE

Abstract

(Zhong and Chen,ACL2020) 使用pipeline方法为实体检测和关系分类设置了两个独立的标签空间，并取得了SOTA。由于pipeline方法不能共享实体抽取和关系抽取的信息，因此作者为了促进两个任务的交互提出了一种可以共享标签空间的方法。作者采用表填充的方法实现，具体来说：输入一张$s\times s$大小的表，这张表包含一个句子中所有的单词对，实体和关系由表格中的正方形和矩形表示（实体：实体内部所有字符都是相同的实体类型标签例如PER；关系：有关系的两个实体的字符都有相同的关系标签），实体都在对角线，关系在非对角线。作者实现了SOTA并且只用了一半的参数，而且速度更快

Figure 1：联合实体关系提取表的示例。每个单元格对应一个单词对。实体是对角线上的正方形，关系是对角线外的矩形。请注意，PER-SOC是无向(对称)关系类型，而PHY和ORG-AFF是有向(非对称)关系类型。

该表准确地表示重叠的关系，例如，PER实体“David Perkins”参与两个关系$(“DavidPerkins”，“Wife”，PER-SOC)$和$(“DavidPerkins”，“California”，PHYS)$。对于每个units，一个相同的双仿射模型预测其标签。联合解码器被设置为寻找最佳正方形和矩形

1 Introduction

人们认为联合模型可能会更好，因为它们可以减轻子模型之间的误差传播，具有更紧凑的参数集，并且统一地编码关于两个任务的先验知识。本文将已有的单独的标签空间转化为统一的标签空间，存在的难点：两个子任务通常被表述不同的学习问题（例如：作为序列标签的实体检测，作为多类分类的关系分类)，并且它们的标签被放置在不同的事物上(例如，词与词对)。

先前的一次尝试(郑等人，2017年)是用一个序列标记模型处理这两个子任务。 设计了一个复合标签集来同时对实体和关系进行编码。然而，该模型的表现力被牺牲了：它既**不能检测重叠关系(即，参与多个关系的实体)，也不能检测孤立的实体(即，没有出现在任何关系中的实体).

作者定义一个新的统一标号空间的关键思想：将实体检测看作关系分类的特例。输入空间是一个二维表，每个条目对应于句子中的一个词对(图1)。联合模型从统一的标签空间(实体类型集和关系类型集的并集)为每个单元指定标签。在图形上，实体是对角线上的正方形，关系是对角线外的矩形。该公式保留了关于现有$entity-ralation$提取场景(例如，重叠关系、有向关系、无向关系)的完整模型表达能力。

基于表格形式，联合实体关系提取器执行两个操作：填充和解码。首先，填表是预测每个词对的标签，类似于依存句法分析中的弧形预测任务。采用双仿射注意机制(Dozat和Manning，2016)来学习词对之间的互动。本文还对表施加了两个结构约束。然后，给出带有标签日志的表填充，本文设计了一种近似联合解码算法来输出最终提取的实体和关系。基本上，它高效地在表中找到分割点来识别正方形和矩形(这也与现有的表填充模型不同，现有的表填充模型仍然应用某些顺序解码并递增地填充表)。

在三个基准测试(ACE04，ACE05，SciERC)上的实验结果表明，与目前最先进的提取器(zhong和Chen，2020)相比，该联合方法取得了与之相当的性能：在ACE04和Science ERC上性能更好，在ACE05.1上更具竞争力；同时，我们的新联合模型在解码速度上更快(比确切的流水线实现快10倍，与近似流水线相当，但性能较低)。它还有一个更紧凑的参数集：与单独的编码器相比，共享编码器只使用一半的参数。

2 Approach

2.1 Task Definition

给定一个句子$s=x_1,x_2,...,x_{|s|}$($x_i$是word)，目的是提取一组实体$\epsilon$和一组关系$\mathcal{R}$。对于关系三元组$(e_1,e_2,l)$，其中$l\in {\mathcal{Y}}_r$是预定义的关系类型，$y_e$、$y_r$表示预定义的实体类型和关系类型的集合。

对于句子$s$维护一个表格$T^{|s|\times |s|}$，其中$|s|$表示句子长度。对于表$T$中的每个单元格$cell(i,j)$，为其分配一个标签$y_{i,j}\in y$，其中$y_e\cup y_r\cup \{\perp \}$，($\perp$表示没有关系)

1. 对于每个实体e：对应的标签$y_{i,j}(x_i\in e.span,x_j\in e.span)$应填写成$e.type$
2. 对于每个关系$r=(e_1,e_2,l)$：对应的标签$y_{i,j}(x_i\in e_1.span,x_j\in e_2.span)$应填写成$l$
3. 对于其他的单元格填写$\perp $

本文将解码实体和关系转化为一个矩形查找问题，查找问题采用联合译码方法来解决。

2.2 Biaffine Model

通过BERT获取上下文表示$h_i$ $\{h_1,...,h)|s|\}=PLM(\{x_1,...,x_{|s|}\})$

为了捕获长范围依存关系，将句子扩展成固定的窗口大小$W$（本文设为200），为了更好的编码表$T $中单词的方向信息，采用了深度双仿射注意力机制。

span start和end：
$$\begin{gathered} h_i^{head}=ML{P}_{head}(h_i), \\ {h}_i^{tail}=ML{P}_{tail}(h_i) \end{gathered}$$
计算每个词span的得分：$$\begin{gathered} g_{i,j}\in {\mathcal{R}}^{|y|} \\ Biaff(h_1,h2)=h_1^T{U}_1{h}_2+U_2(h_1\oplus h_2)+b \\ {g}_{i,j}=Biaff(h_i^{head},h_j^{tail}) \end{gathered}$$
其中$U_1\in {\mathcal{R}}^{|y|\times d\times d}$,$U_2\in {\mathcal{R}}^{|y|\times 2d}$,$b\in {\mathcal{R}}^{|y|}$

2.3 Table Filling

将$g_{i,j}$馈送到Softmax中预测相应标签，从标签空间$y$上产生概率分布：$P(y_{i,j}|s)=Softmax(dropout(g_{i,j}))$

实验中发现对$g_{i,j}$利用dropout可以进一步提高性能,作者称为$logitdropout$

使用交叉熵最小化目标函数：$${\mathcal{L}}_{entry}=-\frac{1}{|s{|}^2}\sum _{i=1}^{|s|}\sum _{j=1}^{|s|}logP(y_{i,j}=j_{i,j}|s)$$，其中$y_{i,j}$是gold label​

2.4 Constraints

目标函数简化了训练过程，实际上还存在一些结构上的约束，实体和关系对应于表中的正方形和矩形，但是目标函数没有显示该约束，本文提出了两个直观的约束，对称和隐含，本文用记号$\mathcal{P}\in {\mathbb{R}}^{|s|\times |s|\times |y|}$表示句子$s$中所有单词对的$P(y_{i,j}|s)$堆叠

**Symmetry(对称)**与实体对应的正方形必须在对角线上，对于对称关系如$(e_1,e_2,l)$和$(e_2,e_1,l)$是等价的，因此在表格上对称关系也是关于对角线对称的(Figure 1所示$("his","wife",PER-SOC)$ and $("wife","his",PER-SOC)$的矩形关于对角线对称）。

标签集$y$分为对称标签集$y_{sym}$和非对称标签集$y_{asym}$

对于矩阵${\mathcal{P}}_{:,:,t}$应该关于每个标签$t\in y_{sym}$的对角线对称，损失为：$${\mathcal{L}}_{sym}=\frac{1}{|s{|}^2}\sum _{i=1}^{|s|}\sum _{|s|}^{j=1}\sum _{t\in y_{sym}}|{\mathcal{P}}_{i,j,t}-{\mathcal{P}}_{j,i,t}|$$

Implication蕴含、包含一个关系存在，那么一定存在两个实体，反之就是，没有两个对应的实体，那么一定不可能存在。从概率的角度看，关系的概率大于每个实体的概率。通过蕴含思想，本文对$\mathcal{P}$施加如下约束：对于对角线上的每个单词，其在实体类型空间 $y_e$ 上的最大可能性不得低于关系类型空间 $y_r$ 上同一行或同一列中的其他单词的最大可能性。

蕴含损失表示为:$${\mathcal{L}}_{imp}=\frac{1}{|s|}\sum _{i=1}^{||s}[\underset{l\in y_r}{\max }\{{\mathcal{P}}_{i,:,l},{\mathcal{P}}_{:i,l}\}-\underset{t\in y_e}{\max }\{{\mathcal{P}}_{i,i,t}\}]$$其中$[u{]}_{\ast }=max(u,0)$是hinge loss.

总的损失:$${\mathcal{L}}_{entry}+{\mathcal{L}}_{sym}+{\mathcal{L}}_{imp}$$

2.5 Decoding

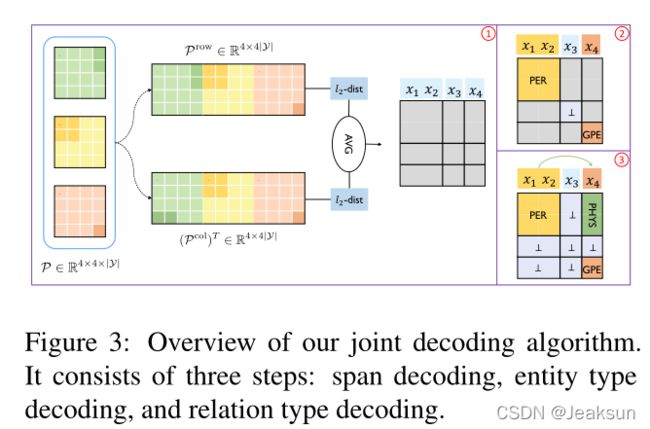
在测试阶段，给定句子s的概率张量$\mathcal{P}\in {\mathbb{R}}^{|s|\times |s|\times |y|}$，从中解码实体的正方形和关系的矩形。受到sun et al 2019的启发，本文提出了一个三步解码算法：1. 解码span(实体或实体间span)。2. 解码每个span的实体类型。3.解码实体对的关系类型。

1. span decoding:一个实体包含的词的行列是相同的，如果相邻的两行/列不同，说明在此处一定有实体边界

   1. 从行的角度出发将$\mathcal{P}\in {\mathbb{R}}^{|s|\times |s|\times |y|}$展平为${\mathcal{P}}^{row}\in {\mathbb{R}}^{|s|\times (|s|\cdot |y|)}$,然后计算行的欧几里得距离$l_2$
   2. 类似的，从列的角度出发根据${\mathcal{P}}^{col}\in {\mathbb{R}}^{(|s|\cdot |y|)\times |s|}$,然后计算列的欧几里得距离
   3. 将两个距离的平均值作为最终距离
   4. 如果距离大于默认的阈值$\alpha$($\alpha =1.4$)则此位置为分割位置(实体边界)，span解码的时间复杂度变成了$\mathcal{O}(|s|)$

2. Entity Type Decoding通过span encoding得出$span(i,j)$,将得到的$i,j$生成正方形来解码实体类型$\stackrel{\wedge }{t}=argma{x}_{t\in y_e\cup \{\perp \}}Aug({\mathcal{P}}_{i:j,i:j,t})$,如果$\stackrel{\wedge }{t}\in y_e$则解码为一个实体,如果$\stackrel{\wedge }{t}=\perp$则$span(i,j)$不是实体。$span(i,j)$在表格中是一个正方形，利用$argmax(\cdot )$取出正方形中所有分数的最大值作为当前span的分数。

3. Relation Type Decoding在实体类型解码后，给定一个实体$e_1=span(i,j)$和另一个实体$e_2=span(m,n)$，解码一个关系$(e_1,e_2,\stackrel{\wedge }{l})$,如果$\stackrel{\wedge }{l}=\perp$,表示没有关系。

   形式上表现为：$\stackrel{\wedge }{l}=argma{x}_{l\in y_r\cup \{\perp \}}Aug({\mathcal{P}}_{i:j,m:m,l})$,如果$\stackrel{\wedge }{l}\in y_r$，解码为一个关系$(e_1,e_2,\stackrel{\wedge }{l})$,如果$\stackrel{\wedge }{l}=\perp$则$e_1,e_2$没有关系。将得到的span两两匹配，得到实体对之间的关系矩形，将矩形中最大的那个位置对应的关系标签作为最终的关系标签。

   3 Experiments

   句子长度设置为200，对于MLP层，将隐藏大小设置为d=150，并使用Gelu作为激活函数。我们使用了β1=0.9和β2=0.9的AdamW优化器。批大小为32，学习率为5e-5，权值衰减为1e-5，线性预热学习率调度器，预热率为0.2。用最多200个epochs(对于SciERC为300个纪元)训练模型，并采用提前停止策略。在Intel®Xeon®W-3175X CPU和NVIDIA Quadro RTX 8000 GPU上进行所有实验。
   

• 没卡的还是看个乐呵吧
  

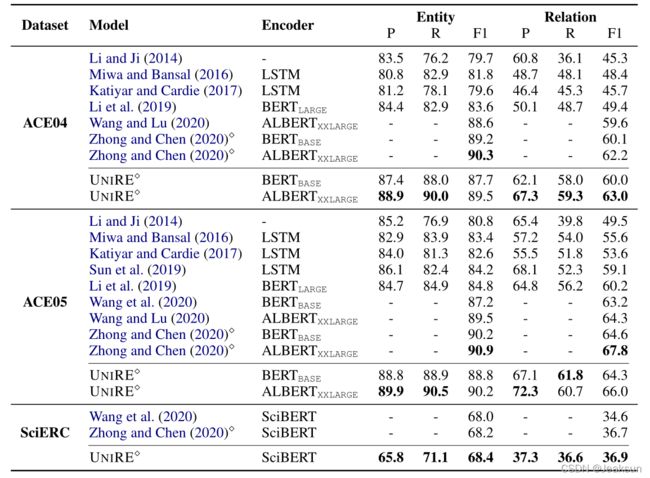
总的来说，UNIRE在ACE04和SciERC上取得了最好的性能，在ACE05上取得了可比的结果。与之前最好的联合模型(Wang and Lu，2020)相比，该模型在ACE04和ACE05上显著提高了实体和关系的性能，即实体的绝对F1分别为+0.9和+0.7，关系的绝对F1分别为+3.4和+1.7。

对于最好的流水线模型(钟和陈，2020)(当前的SOTA)，该模型在ACE04和SciERC上取得了优异的性能，在ACE05上取得了相当的性能。与ACE04/ACE05相比，SciERC的规模要小得多，因此在SciERC上的实体性能大幅下降。由于(钟和陈，2020)是一种流水线方法，其关系绩效受到较差的实体绩效的严重影响。然而，我们的模型在这种情况下受到的影响较小，并且获得了更好的性能。此外，在ACE04上，即使实体结果较差，我们的模型也能获得较好的关系性能。实际上，我们的基础模型(BERTBASE)已经实现了竞争关系绩效，甚至超过了之前基于BERTLARGE(Li et al.，2019)和ALBERTXXLARGE(Wang and Lu，2020)的模型。

3.1 Ablation Study

具体地说，本文实现了一种朴素的比较解码算法，即“硬解码”算法，它以“中间表”作为输入。“中间表”是双仿射模型输出的概率张量P的硬形式，即选择概率最高的类作为每个单元的标签。

为了找到对角线上的实体正方形，它首先尝试判断最大的正方形($|s|\times |s|$)是否为实体。标准只是计算出现在正方形中的不同实体标签的数量，并选择出现频率最高的一个。如果最常用的标签是⊥，我们将正方形的大小缩小1，然后在两个$(|s|-1)\times (|s|-1)$正方形上执行相同的工作，依此类推。为避免实体重叠，如果实体与标识的实体重叠，则将丢弃该实体。为了找到关系，每个实体对都用对应矩形中最频繁的关系标签进行标记。

从消融研究中，我们得到了以下观察结果:

• 移除其中一个额外损失后，性能将随不同程度下降(第2-3行)。具体地说，对称性损失对SCERC有显著影响(实体和关系绩效分别下降1.1分和1.4分)。而去除蕴涵损失会明显损害ACE05(1.0分)的关系绩效。它表明，这两种损失所包含的结构信息对这项任务是有用的。
• 与“Default”相比，“w/o logit Dropout”和“w/o CrossStatement Context”的性能下降幅度更大(第4-5行)。logit dropout可以防止模型过度拟合，而跨句上下文为这项任务提供了更多的上下文信息，特别是对于像SciERC这样的小型数据集。
• hard decoding的性能最差(其关系性能几乎是“default”的一半)(第6行)。最主要的原因是“硬解码”将实体和关系分开解码。

结果表明，该译码算法综合考虑了实体和关系，对译码具有重要意义

3.2 Error Analysis

我们进一步分析了用于关系提取的其余错误，并给出了五种错误的分布情况：

​ 跨度拆分错误(SSE)、实体未找到(ENF)、实体类型错误(ETE)、关系未找到(RNF)、和关系类型错误(RTE)

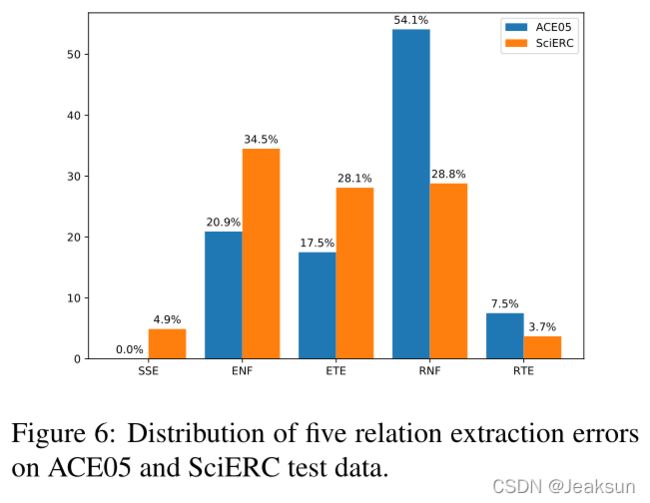
SSE”所占的比例相对较小，这证明了我们的跨度解码方法的有效性。

此外，无论是实体还是关系，“未发现错误”的比例都明显大于“类型错误”的比例。最主要的原因是填表存在类不平衡问题，即⊥的数量远远大于其他类。