AB测试——原理介绍（中心极限定理、大数定理、假设检验、两类错误）

作为AB测试的学习记录，本文主要整理总结了AB测试背后的数学原理和一些概念解释。

---

1、控制变量法

基于控制变量法的思想，通过对比两组样本（实验组和对照组）的表现是否有差异，从而验证“变量”的作用。

借用中学生物课上的例子：探究种子萌发的环境条件的实验。

为了确定阳光对种子萌发有影响，需要确保除光照外所有环境变量一致。实验需要设置实验组和对照组，其中，对照组是正常接受光照的种子（没有其他特殊待遇）；实验组是黑暗环境下的种子（有特殊待遇：没有光照）。

最后通过对比两组种子的发芽情况，得出“阳光对种子是否有影响”的结论。此外，还可以对比水分、温度等等环境变量对种子萌发的影响。

同理， 在实际的商业环境中，用户就像是这些待发芽的种子，我们可以通过控制产品设计、营销策略、推荐算法等等“变量”，去提高它们的“萌芽率”——活跃度、留存率、消费金额等等。因此，我们需要进行AB实验去检验各种策略、设计对公司的运营是有效的。

简言之，AB测试是一种评估运营方案是否有效的实验方法。 当不确定两种（或者多种）待选方案中哪个表现更好时，通过直接的实验手段去验证，找出最佳的解决方案。

但这种实验的前提是，样本量足够且变量可以控制。若样本量不足，例如刚上架的APP没有多少注册用户也就没有实验的必要性。

2、中心极限定理VS大数定理

2.1 中心极限定理

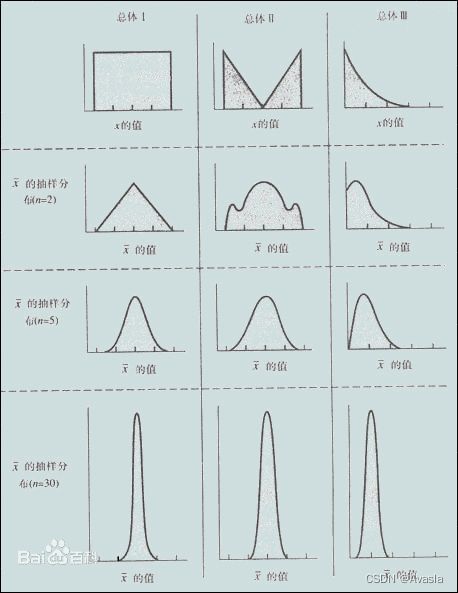
随着试验次数的增加，一组独立同分布的变量的均值可以近似看作服从正态分布，且方差也会随着试验次数的增加而减小。简言之，无论总体是什么分布，只要样本量足够大，样本的均值分布都会趋于正态分布。

具体的验证过程可以查看笔记《Python验证中心极限定理》。

样本和总体都呈正态分布，样本量的均值和总体均值一致。 当N固定时，样本的均值和总体一致，样本的方差等于总体的方差/N

独立同分布：指随机过程中，任何时刻的取值都为随机变量，如果这些随机变量服从同一分布，并且互相独立。比如掷色子，第一次和第二次掷出的结果都不会相互影响，而且结果是随机的。

2.2 大数定理

大数定律的核心在于将随机变量X所对应的随机试验重复多次，随着试验次数的增加，X的均值会愈发趋近于E(X)。即，样本量越大，越靠近总体。

2.3 两个原理的区别

中心极限定理是说无论抽样分布如何均值服从正态分布；而大数定律根本和正态分布无关，是说样本大了抽样分布近似总体分布。

3、假设检验

1） 提出假设

• 原假设 (null hypothesis，H0)：需要拒绝掉的假设，我们不希望看到的结果：新方案对核心指标不会有显著性影响。
• 备择假设 (alternative hypothesis，H1)：和原假设相反的假设，是我们想要的结果：新方案对核心指标有显著性影响。

PS： 在提出假设这一步，我个人的难点是总记不住两个假设的定义。 后面知道了一句顺口溜：“越小越拒绝"，意思是P值越小，越拒绝原假设。然后联想推出：P值越小越好，所以在对P值进行判断时，记住不要大的数，越接近0越好。P值越小，我们越要拒绝的原假设。既然原假设是用来拒绝的，那么原假设就是我们不想要的那个结果。

2.1） 选定检验方向

根据备择假设确定检验方向：

• 双侧检验：备择假设没有特定的方向性，形式为“≠”这种检验假设称为双侧检验

• 单侧检验：备择假设带有特定的方向性，形式为”>””<“的假设检验，称为单侧检验。 其中备择假设 “<“称为左侧检验； “>”称为右侧检验

2.2） 选定检验方法

常用的检验方法有 t检验 和 z检验。

判断使用什么检验方法，我们需要看样本量和总体方差是否已知，判断的流程如下图所示：

**一般情况下，绝对值指标用T检验，相对值指标用Z检验。**因为绝对指标的的总体方差，需要知道每一个用户的值，这个在AB实验中肯定不可能。而相对值指标是二项分布，可以通过样本量的值计算出总体的值，就如同10W人的某页面点击率是10%，随机从这10W人中抽样1W人，这个点击率也是10%一样。

3） 结果判断

显著性水平：
指当原假设实际上正确时，检验统计量落在拒绝域的概率，简单理解就是犯弃真错误的概率。
显著性水平α越小，犯第I类错误的概率自然越小，一般取值：0.01、0.05、0.1等。

• 当给定了检验的显著水平a=0.05时，进行双侧检验的Z值为1.96。
• 当给定了检验的显著水平a=0.01时，进行双侧检验的Z值为2.58。
• 当给定了检验的显著水平a=0.05时，进行单侧检验的Z值为1.645。
• 当给定了检验的显著水平a=0.01时，进行单侧检验的Z值为2.33。

一般情况下，都是选择a=0.05作为判断：

• 如果P≤α，那么拒绝原假设
• 如果P>α，那么不能拒绝原假设

拒绝域： 拒绝域是由显著性水平围成的区域。

检验统计量：
对原假设和备择假设作出决策的某个样本统计量，称为检验统计量。
t-test和z-test对应的检验统计量就是 t值 和 z 值。

P值：
P值是用来判定假设检验结果的一个参数，反映某一事件发生的可能性大小，即P值是一个概率值。统计学根据显著性检验方法所得到的P值，一般以P<0.05 为有统计学差异。

---

4. 两类错误

弃真错误：也叫第I类错误或α错误。它是指原假设实际上是真的，但通过样本估计总体后，拒绝了原假设。明显这是错误的，我们拒绝了真实的原假设，所以叫弃真错误，这个错误的概率我们记为α。（这个值也是显著性水平，在假设检验之前我们会规定这个概率的大小。）

取伪错误：也叫第II类错误或β错误。它是指原假设实际上假的，但通过样本估计总体后，接受了原假设。明显者是错误的，我们接受的原假设实际上是假的，所以叫取伪错误，这个错误的概率我们记为β。把统计功效定义为1-β，一般情况下， β 取值0.2，则统计功效的取值为0.8。

举个栗子：一类错误就是这个产品不能给我们带来收益，但是错误判断它可以带来收益 。这个会导致坏产品上线。二类错误就是，这个产品实际上是好产品，能给我们带来收益，但是我们错误认为它不能赚钱。这个错误会导致拒绝好的产品上线（取伪错误）。 相比之下，一类错误更不能接受。我们宁愿让10个好产品不上线，也不能让1个坏产品上线了，因为一个坏的产品可能带来无法挽回的客户损失。

引申问题： 为什么原假设是"想要拒绝的假设"呢？
答： 因为原假设被拒绝如果出错的话，只能犯第I类错误，而犯第I类错误的概率已经被规定的显著性水平所控制。