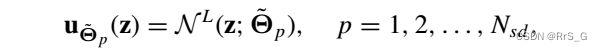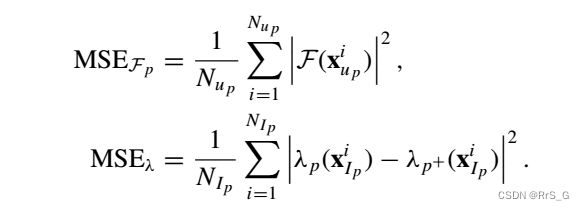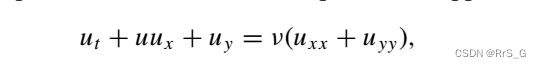论文理解:“Conservative physics-informed neural networks on discrete domainsfor conservation laws: Appl“

译：守恒定律离散域上的保守物理信息神经网络:在正问题和反问题中的应用

-- Comput. Methods Appl. Mech. Engrg. 365 (2020)

---

目录

一、引言

二、问题设置

三、方法

四、数值实验

4.1、Viscous Burgers 方程

4.2、Korteweg–de Vries 方程

4.3、不可压缩Navier–Stokes方程

4.4、逆问题：二维无粘Burgers方程

---

一、引言

        PINN与传统的数值方法(如有限元方法和有限差分方法)有着本质的不同，后者的控制偏微分方程最终会在计算域上离散。然而，PINN有两个限制。第一个是解的精度，即绝对误差不会低于10^-5左右的水平，这是由于高维非凸优化问题的求解精度不高，可能导致局部极小值。第二个限制是与深度神经网络和长时间集成的控制偏微分方程相关的大训练成本。

        本文作者提出了一种基于离散子域的保守物理信息神经网络(cPINN)，在每个子域使用单独的PINN，然后通过相应的保守量(如通量)缝合所有子域，这使得该方法具有独特性。给定有限的、可管理的大小的子域，可以使用cpu和gpu集群执行大规模并行计算。这是解决维数魔咒问题的最佳策略，维数魔咒与高维问题的数值逼近有关，无论是计算成本还是内存需求。因此，本文提出的cPINN方法可以有效地处理高维问题。

二、问题设置

一般方程形式如下：

满足适当的边界条件和初始条件. 

对于式(1)，残差为

三、方法

可伸缩参数

        作者在每一层隐藏层引入可伸缩参数，与激活函数一起逐层应用，其中n是比例因子。逐层引入附加参数会改变每个隐层激活函数的斜率，从而提高训练速度。

这种局部自适应激活函数增强了网络的学习能力，尤其是在训练早期。本文作者对所有隐藏层使用比例因子n = 5，并初始化. 

于是，网络过程为：

所以，网络的可更新参数比之前多了一项可伸缩参数。

---

        图1给出了cPINN算法的原理图，除了NN和PDE部分，附加的界面条件也对损失函数有贡献。界面条件包括强形式的通量连续性条件，以及沿共同界面两个神经网络给出的平均解。虽然不需要强制平均解沿共同界面，作者通过数值实验表明，它将大大加快收敛速度。

        图2给出了PINN和cPINN方法的示意图。与PINN不同的是，cPINN将域划分为若干小的子域，在这些子域中，可以使用具有不同架构的完全不同的神经网络(这里称之为子PINN网络)来获得相同底层PDE的解。这种区域分解还可以很容易地实现网络的并行化，这对于实现计算效率非常重要。该算法的另一个特点是，可以根据对每个子域的解的规律性的一些直观的知识，自由地选择网络超参数，如优化方法、激活函数、网络的深度或宽度。对于平滑区域，可以使用浅网络，而深度网络可以用于一个复杂的解的区域。

        cPINN公式实际上考虑了各子域界面的通量连续性，这是受守恒定律的启发。利用适当的界面条件，将各子域的所有解拼接起来，重建出整个解。在cPINN中，神经网络在第p个子域的输出为

最终的解为：

子域损失函数及优化算法

        cPINN的损失函数按子域定义，其结构与每个子域的PINN损失函数相似，但赋予了接口条件。对于正问题，作者定义第p个子域的损失函数为

另：

和分别是子域和上两个不同神经网络给出的公共接口法线的接口通量，"+"表示临近的子域。u沿共同界面的平均值为：

注：的选取很关键。

反问题

        以上关注的是正问题，在由已知解确定常系数的反问题中，第p个子域的损失函数为

其中：

伪代码如下：

四、数值实验

4.1、Viscous Burgers 方程

方程如下：

初始条件u(x, 0) = - sin(nx)，边界条件u(-1, t) = u(1, t) = 0, ν = 0.01/π。针对该问题，将域划分为四个子域，各子域的接口位置x =[-0.2, 0.1, 0.5]。

表1显示了用于求解一维Burgers方程的两种不同的神经网络结构。：

在顶层表中，隐藏层的数量和每层神经元的数量是相同的，所有子域使用相同的激活函数tanh。在下面的表格中，隐藏层的数量和神经元的数量是不同的。此外，在子域中使用了不同的激活函数。对于这两种架构，所有子域中的残差点是相同的。这两种架构都给出了可比较的结果，即使它们的相对L2误差(如表1所示)在每个子域中是相同的顺序。cPINN模拟进行了15000次迭代。

图4显示了Burgers方程解的等高线图，其中左上角的图显示了子域编号系统。cPINN和逐点误差预测的解分别由上中图和右上图给出。cPINN给出的最大逐点误差出现在高梯度区域附近。预测解中的白色水平线表示界面位置。

4.2、Korteweg–de Vries 方程

一维KdV方程为：

其中v=0.0025.

表3给出了KdV方程的cPINN架构。

图6给出了通过PINN(中)和cPINN(下)得到的精确解(上)、预测解以及逐点误差。

水平白线为x = -0.74处的界面位置，将区域分为两个子区域。

图7给出了PINN和cPINN在不同t位置的解的比较，其中cPINN相对于PINN的精度是很明显的。

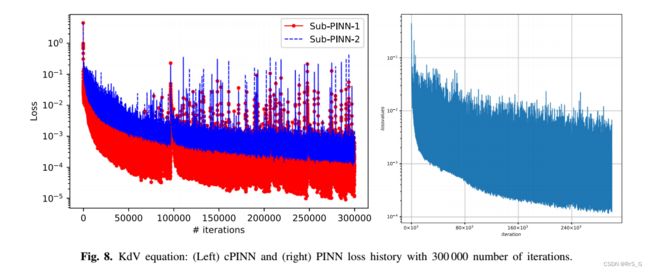
最后，图8给出了cPINN(左)和PINN(右)在迭代次数上的损失历史。

4.3、不可压缩Navier–Stokes方程

方程：

表7显示了用于每个子域模拟的神经网络体系结构。

自适应激活函数为tanh，学习率为0.0006。界面在x轴和y轴上的位置分别为[0.2,0.8]和[0.2,0.45,0.8]，每个接口的接口点数为100。

结果如下：

4.4、逆问题：二维无粘Burgers方程

二维无粘Burgers方程为

满足边界条件：

原文参考文献[30]给出了a = 1和b = -1情况的精确解，它在x = 0处具有稳定的不连续。在cPINN算法中，不提供原方程，如下所示

要做的就是找出粘度系数v的值。

        12个子域中从1到12的隐藏层数为[6,3,3,6,3,3,6,3,6,3,3,3,3,3,3,3,6,3,3,6,3,3]，每层有20个神经元，每个子域对应的v的初始值为[1,2,3,4,5,6,7,8,9,10,11,12]/3。图27显示了所有12个子域中v随迭代次数的变化。左图为干净数据，右图为有1%噪声的数据。

 

两种情况在整个域内对应的相对L2误差如表12所示。

在这两种情况下，网络都能正确识别粘度v值。此外，可以观察到，训练数据中噪声的存在减少了v向其准确值的收敛。干净的数据大约需要9000次迭代，而含有1%噪声的数据大约需要13000次迭代才能收敛。

代码(非官方)：AmeyaJagtap/Conservative_PINNs: We propose a conservative physics-informed neural network (cPINN) on decompose domains for nonlinear conservation laws. The conservation property of cPINN is obtained by enforcing the flux continuity in the strong form along the sub-domain interfaces. (github.com)