Transfer learning based multi-fidelity physics informed deep neural network论文笔记
论文信息
题目:Transfer learning based multi-fidelity physics informed deep neural network
作者:Souvik Chakraborty
期刊会议: Machine Learning (cs.LG); Computational Physics (physics.comp-ph)
年份:2020
论文地址:
代码:
基础补充
内容
动机
动机:
- 基于某些假设和近似,一些控制方程可以得到,但是建立的这个模型属于low-fidelity模型
- 通过实验,可以得到high-fidelity data,但是当数据收集昂贵且耗时,得到大量high-fidelity data 非常困难
- 同时利用low-fidelity模型与少量的high-fidelity data
- One possible solution to the difficulties raised above resides in multi-fidelity schemes where data fusion tech- niques are used to combine high-fidelity and low-fidelity data.
前人工作:
- The most popular multi-fidelity schemes are perhaps the multi-level Monte Carlo (MLMC) methods. MLMC fails when the low-fidelity and high-fidelity data have a space-dependent, complex and nonlinear correlations.
- The field of artificial intelligence and machine learning has recently witnessed a huge boom and its influence can also be observed in the multi-fidelity approaches. De et al 1 developed two multi-fidelity approaches by using deep neural networks.
- While the first framework uses transfer learning, the second framework utilizes bi-fidelity weighted learning. Meng and Karniadakis 2, on the other hand, proposed a composite neural network that is trained based on multi-fidelity data.
Based on the discussion above, (at least) two salient conclusions can be drawn about the existing multi-fidelity approaches:
- First, the existing multi-fidelity approaches assume the low-fidelity solver to be computationally efficient so that one can generate sufficient low-fidelity data.
- Second, the physics informed multi-fidelity approaches proposed in 3 assume that the exact physics cor- responding to the high-fidelity data is known. This is not necessarily true. There are problems where the underlying physics is unknown [1]. Also, the apparently known governing equations are often derived based on
创新:
问题定义
The probability of failure of the system can be calculated as
P f = P ( Ξ ∈ Ω f ) = ∫ Ω f d F Ξ ( ξ ) = ∫ Ω I Ω f d F Ξ ( ξ ) \begin{aligned} P_{f}=\mathbb{P}\left(\boldsymbol{\Xi} \in \Omega_{f}\right) &=\int_{\Omega_{f}} \mathrm{d} F_{\Xi}(\boldsymbol{\xi}) \\ &=\int_{\Omega} \mathbb{I}_{\Omega_{f}} \mathrm{d} F_{\Xi}(\boldsymbol{\xi}) \end{aligned} Pf=P(Ξ∈Ωf)=∫ΩfdFΞ(ξ)=∫ΩIΩfdFΞ(ξ)
数据点的数量 N h N_{h} Nh意义重大,可以直接训练代理模型, M : ( ξ , x , t ) → u \mathcal{M}:(\xi, x, t) \rightarrow u M:(ξ,x,t)→u然后用它来评估上式失败的概率
然而,在现实中,可以执行的实验室实验数量是有限的,因此,可用的数据点的数量往往不足以训练一个替代模型。为了补偿只有有限数量的高保真数据可用这一事实,我们考虑了系统的近似(低保真)控制方程:
I c ( ξ ) = { 1 if ξ ∈ c 0 if ξ ∉ c \mathbb{I}_{c}(\boldsymbol{\xi})=\left\{\begin{array}{ll}1 & \text { if } \quad \boldsymbol{\xi} \in c \\ 0 & \text { if } \quad \boldsymbol{\xi} \notin c\end{array}\right. Ic(ξ)={10 if ξ∈c if ξ∈/c
u t + h ( u , u x , u x x , … ; ξ ) = 0 u_{t}+h\left(u, u_{x}, u_{x x}, \ldots ; \boldsymbol{\xi}\right)=0 ut+h(u,ux,uxx,…;ξ)=0
方法
- 用常/偏微分方程给出了低逼真度模型,该模型不需要低保真度数据;相反,初始的低保真度模型直接训练基于问题的(近似)物理。这是通过利用最近开发的物理信息深度学习算法来实现的,通过这样的设置,一些重要的物理定律,比如低保真度模型中存在的不变性和对称性,将会被深度学习框架固有地捕捉到。
- 然后使用迁移学习和可用的高保真数据更新训练好的
Physics-informed deep neural networks
-
对于现在一些纯数据驱动的DNN来说,需要大量的高可信度的数据参与训练。然而,对于目前的这片paper工作来说,焦点集中在很少能获得高保真数据的问题上。因此,直接应用数据驱动的DNN不太可能产生令人满意的结果。所以,为了解决数据驱动的DNN对训练数据的过度依赖,PINN被提出。
-
PINN有两个主要的优点:首先,与数据驱动的DNN等其他可靠性分析工具不同,PI-DNN不需要仿真数据。这将大大降低计算成本。其次,通过满足系统的控制微分方程来训练PI-DNN。因此,满足了不变性和对称性等物理特性。
-
但是对于PINN求解,准确的控制方程是已知的,但是在科学和工程中存在着许多控制微分方程4未知的情况。即使控制方程是已知的,它经常是基于某些假设和近似。
Proposed approach
3.1节中的数据驱动的DNN和3.2节中的PINN都不能解决第2节中定义的可靠性分析问题
- 数据驱动的DNN失败是因为高保真数据的数量, N h N_{h} Nh非常少。另一方面,PI-DNN不能作为Eq.(7)中的控制微分方程,只能近似地表示实际情况。
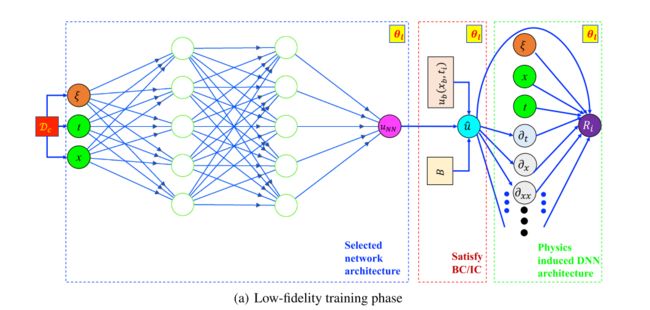
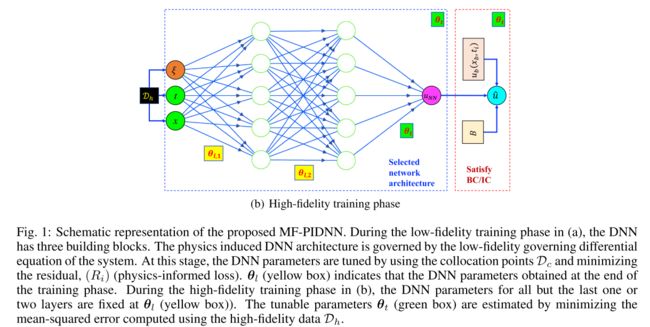
- A multi-fidelity Aphysics informed deep neural network (MF-PIDNN) is presented in this section. MF-PIDNN utilizes the concepts of both data-driven and physics informed DNNs. Unlike available multi-fidelity frameworks, the proposed MF-PIDNN does not assume that generating low-fidelity data is trivial. In fact, no low-fidelity data is needed for the MF-PIDNN presented here.
- The key consideration of any multi-fidelity framework is associated with discovering and exploiting the relation be- tween the low-fidelity and high-fidelity model/data. In most of the frameworks available in the literature, this is achieved by using two surrogates; the first surrogate is trained based on the low-fidelity data and the second surrogate is used to find the functional relation between the low-fidelity and the high-fidelity data. This paper takes a separate route; instead of using two DNNs, a single DNN is first trained for the low-fidelity model and then updated based on the high-fidelity data.
方法:主要分成两步
- 第一步,使用PINN求解low-fidelity模型
- 第二步,然后用high-fidelity data D h x \mathcal{D}_{h x} Dhx更新low-fidelity模型(将low-fidelity模型网络参数作为初始化,用 D h x \mathcal{D}_{h x} Dhx只更新最后一个或两个层对应的参数)
优势(使用了迁移学习)
- First, because of transfer learning, the number of parameters to be updated is reduced. This in turn, accelerates training of the DNN.
- Second, freezing the parameters of the initial layer ensures that the features learned/extracted from the low- fidelity model are retained in the network.
- Thirdly, transfer learning also ensures that the DNN does not overfit the high-fidelity data, Dh.
实验
our numerical examples are presented to illustrate the performance of the proposed approach. A wide variety of examples involving single and multiple stochastic variables, linear and non-linear problems, ordinary and partial differential equations are selected
实验1
d u l d t = − Z u l \frac{\mathrm{d} u_{l}}{\mathrm{d} t}=-Z u_{l} dtdul=−Zul
满足下面初值:
u l ( t = 0 ) = 1.0 u_{l}(t=0)=1.0 ul(t=0)=1.0(21)
high-fidelity model:
u h = t sin ( t ) [ log ( u l 4 ) ] 2 + 15 t 3 + 1.0 u_{h}=t \sin (t)\left[\log \left(u_{l}^{4}\right)\right]^{2}+15 t^{3}+1.0 uh=tsin(t)[log(ul4)]2+15t3+1.0(22)
The relation between the high-fidelity u h u_{h} uh and the low-fidelity u l u_{l} ul is non-linear. The limit-state function for this problem is defined as
J ( Z , t t ) = u h ( Z , t t ) − u 0 \mathcal{J}\left(Z, t_{t}\right)=u_{h}\left(Z, t_{t}\right)-u_{0} J(Z,tt)=uh(Z,tt)−u0 (23)
For this example, t t = 1.0 t_{t}=1.0 tt=1.0 and u 0 = 18.0 u_{0}=18.0 u0=18.0 is considered. It is assumed that 15 samples from the high- fidelity model is available,and for each of the 15 high-fidelity samples, the observations are available at t = [0.0, 1.0]. Note that the data-generation process, i.e., Eq. (23) is not known. MF-PIDNN only have access to the high-fidelity data and the low-fidelity model in Eq. (21).
Process:
- First step:
u ^ = t ⋅ u N N + 1.0 \hat{u}=t \cdot u_{N} N+1.0 u^=t⋅uNN+1.0
The residual for training the low-fidelity DNN is
R i = d u ^ i d t + Z i u ^ i R_{i}=\frac{\mathrm{d} \hat{u}_{i}}{\mathrm{d} t}+Z_{i} \hat{u}_{i} Ri=dtdu^i+Ziu^i - After training the physics-informed low-fidelity DNN, the next step is to update the model based on the high-fidelity data by using the transfer learning.
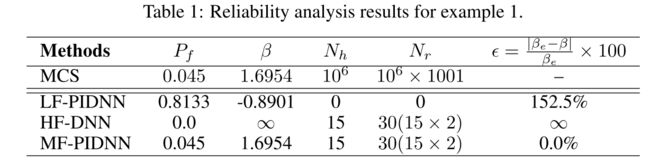
Table 1 shows the results obtained using MCS and MF-PIDNN
- The results obtained using MF-PIDNN matches exactly with the MCS results.
- To show the utility of the proposed approach, results obtained using only the low-fidelity PI-DNN and the high-fidelity DNN are also presented. Both low-fidelity PI-DNN and high-fidelity DNN are found to yield erroneous results.
To that end, it is assumed that for each of the 15 high-fidelity samples, observations are availablet = [0.0, 0.5, 0.9], and the objective is to compute the reliability of the system att = 1.0. The results obtained are shown in Table 2. - Compared to the results presented in Table 1, slight deterioration in the results have been observed;This is expected because this is an extrapolation problem.
- Nonetheless, the results obtained are still significantly more accurate as compared to HF-DNN and LF-PIDNN.

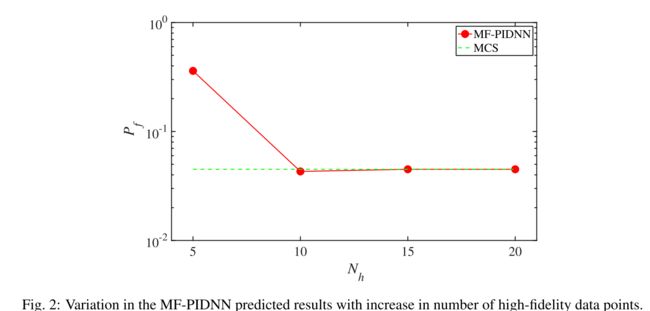
Finally, the performance of the MF-PIDNN withvariation in the number of high-fidelity data point, N h N_{h} Nh is investigated. For each realization of Z, the responses are observed att = [0.0, 1.0]and the probability of failure at t t = 1.0 t_{t}=1.0 tt=1.0is computed. The variation of the MF-PIDNN predicted probability of failure is shown in Fig. 2. - With an increase in N h N_{h} Nh, the MF-PIDNN predicted probability of failure converges to the MCS solution.
- The HF-DNN results, up to N h = 20 N_{h}=20 Nh=20, yields erroneous results (not shown in Fig. 2). This is because, with only observations at two time-instants, the DNN fails to predict the trend of the limit-state function. MF-PIDNN, on the other hand, learns the trend from the physics of the problem and then update itself based on
实验2
The low-fidelity model, on the other hand, is considered to be
( u l ) t = ν ( u l ) x x \left(u_{l}\right)_{t}=\nu\left(u_{l}\right)_{x x} (ul)t=ν(ul)xx
The high-fidelity model for this problem is
( u h ) t + u h ( u h ) x = ν ( u h ) x x \left(u_{h}\right)_{t}+u_{h}\left(u_{h}\right)_{x}=\nu\left(u_{h}\right)_{x} x (uh)t+uh(uh)x=ν(uh)xx
The boundary and the initial conditions:
u h ( t , x = − 1 ) = 1 + δ u h ( t , x = 1 ) = − 1 u h ( t = 0 , x ) = − 1 + ( 1 + x ) ( 1 + δ 2 ) \begin{array}{c} u_{h}(t, x=-1)=1+\delta \quad u_{h}(t, x=1)=-1 \\ u_{h}(t=0, x)=-1+(1+x)\left(1+\frac{\delta}{2}\right) \end{array} uh(t,x=−1)=1+δuh(t,x=1)=−1uh(t=0,x)=−1+(1+x)(1+2δ)
Process:
- u ^ = u h ( t = 0 , x ) + t ( 1 − x ) ( 1 + x ) u N N \hat{u}=u_{h}(t=0, x)+t(1-x)(1+x) u_{N N} u^=uh(t=0,x)+t(1−x)(1+x)uNN
R i = ( u ^ t ) i − ν ( u ^ ) x x ) i \left.R_{i}=\left(\hat{u}_{t}\right)_{i}-\nu(\hat{u})_{x x}\right)_{i} Ri=(u^t)i−ν(u^)xx)i
Along with MCS and MF-PIDNN results, LF-PIDNN and HF- DNN predicted results are also presented.
- Similar to the previous example, both probability of failure and reliability index are reported. It is observed that MF-PIDNN predicted results are extremely close to the MCS results.
- HF- DNN and LF-PIDNN, on the other hand, yields erroneous results. Fig. 3 shows the performance of MF-PIDNN with increase in Nt (i.e, number of time-steps at which high-fidelity data is available).
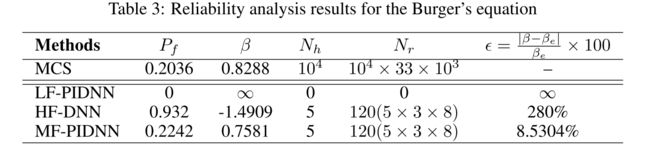
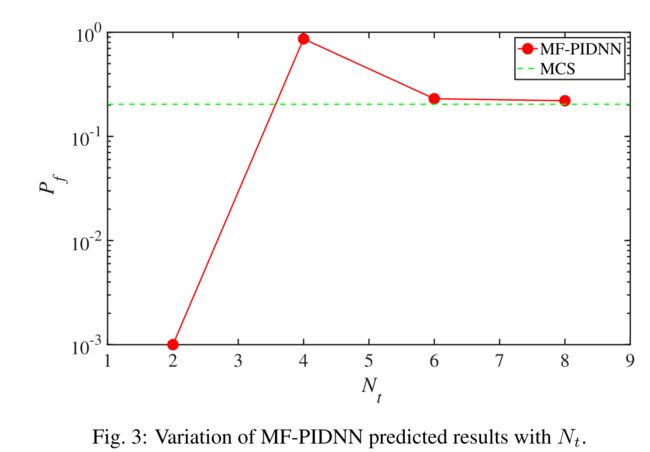
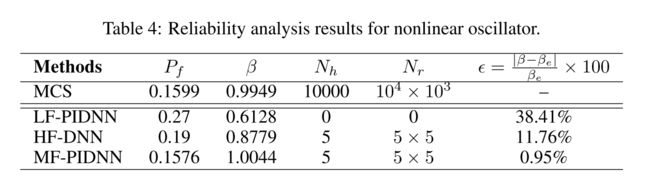
Nonlinear oscillator.
Methods
The variation of probability of failure with threshold x0 is shown in Fig. 4.
- Corresponding to all the thresholds, the MF-PIDNN predicted results matches closely with the MCS results. This indicates that the proposed MF-PIDNN is able to capture the response over the whole domain.

结论
In this paper, a multi-fidelity physics informed deep neural network (MF-PIDNN) is presented. The proposed approach is ideally suited for problems where the physics of the problem is known in an approximate sense (low-fidelity physics) and only a few high-fidelity data is available.
- MF-PIDNN blends the concepts of
physics-informedanddata-driven deep learning; - The primary idea is to first train a low-fidelity deep learning model based on the available approximate physics and then use transfer learning to update the model based on the high-fidelity data.
There are two distinct advantages of MF-PIDNN.
- First, the low-fidelity model is directly trained from the physics of the problem and hence, no low-fidelity data is needed in this framework. - Second, because of the physics-informed framework within MF- PIDNN, the proposed approach is able to capture some of the physical laws that are present in the approximate model.
不足
不懂
可借鉴地方
Subhayan De, Jolene Britton, Matthew Reynolds, Ryan Skinner, Kenneth Jansen, and Alireza Doostan. On transfer learning of neural networks using bi-fidelity data for uncertainty propagation. arXiv preprint arXiv:2002.04495, 2020. ↩︎
Xuhui Meng and George Em Karniadakis. A composite neural network that learns from multi-fidelity data: Ap- plication to function approximation and inverse pde problems. Journal ofComputational Physics, 401:109020, 2020 ↩︎
Dehao Liu and Yan Wang. Multi-fidelity physics-constrained neural network and its application in materials modeling. Journal ofMechanical Design, 141(12), 2019. ↩︎
Steven L Brunton, Joshua L Proctor, and J Nathan Kutz. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proceedings ofthe national academy ofsciences, 113(15):3932– 3937, 2016. ↩︎