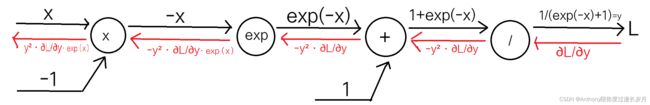“深度学习”学习日记。误差反向传播法--加法层、乘法层、激活函数层的实现

2023.1.16

1、加法层、乘法层：

前两篇文章都在讲述理论，今天实现代码操作：关于加法节点，乘法节点的内容在这篇文章。

https://blog.csdn.net/m0_72675651/article/details/128695488

在以后的学习中，将把构建神经网络的“层”实现为一个类。这里的“层”是指神经网络中功能的单位。

这样写感觉到可以让代码变得美观一点，而更容易找出错误并修改

class Addyer:  # 加法节点
    def __init__(self):
        pass

    def forward(self, x, y):
        out = x + y
        return out

    def backward(self, dout):
        dx = dout * 1
        dy = dout * 1
        return dx, dy


class Mullyer:  # 乘法节点
    def __init__(self):  # __init__() 中会初始化实例变量
        self.x = None
        self.y = None

    def forward(self, x, y):
        self.x = y
        self.y = x
        out = x * y

        return out

    def backward(self, dout):
        dx = dout * self.x
        dy = dout * self.y

        return dx, dy

现在用代码实现了，加法层和乘法层，所以我们用代码解决这个问题：

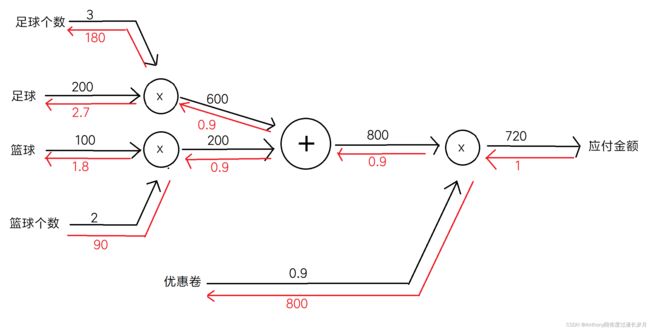
利用反向传播法，求解，篮球、足球分别对应付金额上涨1元的影响是多少？

 代码实现：

class Addyer:  # 加法节点
    def __init__(self):
        pass

    def forward(self, x, y):
        out = x + y
        return out

    def backward(self, dout):
        dx = dout * 1
        dy = dout * 1
        return dx, dy


class Mullyer:  # 乘法节点
    def __init__(self):  # __init__() 中会初始化实例变量
        self.x = None
        self.y = None

    def forward(self, x, y):
        self.x = y
        self.y = x
        out = x * y

        return out

    def backward(self, dout):
        dx = dout * self.x
        dy = dout * self.y

        return dx, dy


discout = 0.9

basketball = 100  # b
football = 200  # f

basketball_num = 2
footbal_num = 3

# 求解问题时 因为乘法层的反向传播需要正向传播的参数
m = Mullyer()
m1 = Mullyer()
m2 = Mullyer()
a = Addyer()

b_price = m2.forward(basketball, basketball_num)
f_price = m1.forward(football, footbal_num)
b_f_price = a.forward(b_price, f_price)
final_price = m.forward(discout, b_f_price)

print(final_price)  # 720
# 求解 应付金额上涨1元 delta=1
# 篮球得影响
delta = 1
ddiscount, db_f_price = m.backward(delta)
dbaskbetball1, dfootball1 = a.backward(db_f_price)
dbaskbetball, dbaskbetball_num = m2.backward(dbaskbetball1)
dfootball, dfootball_num = m1.backward(dfootball1)

print(db_f_price)  # 800
print(dfootball1)  # 0.9
print(dbaskbetball, dbaskbetball_num)  # 1.8 90.0
print(dfootball, dfootball_num)  # 2.7 180.0

综上，计算图中层的函数计算层实现计算复杂导数的代码简单，接下来要学习激活函数层的代码实现；

2，激活函数层：

我们回忆一下  函数,  ，易得 其偏导数 

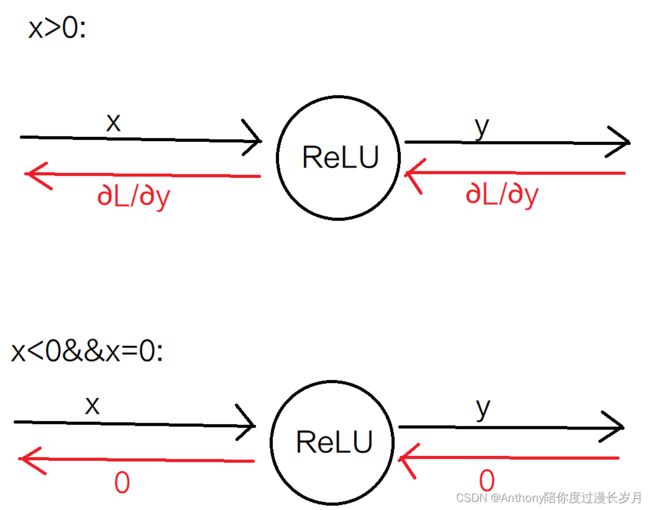
在正向传播时，如果x大于0，则反向传播时，上游的x会原封不动的传递给下游；反之，正向传播时，如果x小于等于0的话，则反向传播中传给下游的信号将停在此处。

用计算图表示：

 

import numpy as np


class ReLU:
    def __init__(self):
        self.mask = None

    def forward(self, x):
        self.mask = (x <= 0)
        out = x.copy()
        out[self.mask] = 0

        return out

    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout

        return dx


arr = np.arange(-3, 3).reshape(2, 3)
print(arr)
a = ReLU()
print(a.forward(arr))
mask = (arr <= 0)
print(mask)

输出结果：

[[-3 -2 -1]
 [ 0  1  2]]
[[0 0 0]
 [0 1 2]]
[[ True  True  True]
 [ True False False]]

通过输出结果，我们可以很清楚的知道mask的作用是一个开关 ， 一个bool值开关。因此，反向传播中会使用正向传播保存的mask，True为0，false为1。

我们们使用网络的学习，这一部分学习过ReLU函数不适合作为激活函数 https://blog.csdn.net/m0_72675651/article/details/128602009

所以我们接下来来实现sigmoid函数 

回忆一下sigmoid函数： 

正先传播的话是这样：

 反向传播时有大学问，得分解详细讲述：

“ /  节点”： 正向传播时是  ，所以在反向传播时，  ；

“ + 节点”： 学习过他有上游会原封不动得传递到下游；

“exp 节点”：在正向传播时表示y=exp（x），由指数函数的数学解析式可得   ；

“ x 节点”： 我们得将正向传播的值翻转后再做乘法运算；

用计算图表示：

或许可以进一步处理：   。

import numpy as np


class Sigmoid:
    def __init__(self):
        self.out = None

    def forward(self, x):
        out = 1 / (1 + np.exp(-x))
        self.out = out

        return out

    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out

        return dx


arr = np.arange(-3, 3).reshape(2, 3)
s = Sigmoid()
s1=s.forward(arr)
print(s.forward(arr))
print(s.backward(arr))

 输出结果：

[[0.04742587 0.11920292 0.26894142]
 [0.5        0.73105858 0.88079708]]
[[-0.13552998 -0.20998717 -0.19661193]
 [ 0.          0.19661193  0.20998717]]

 在正向传播时，用到了实例out，在反向传播时我们也用到了实例out，这样我们可以先进行一次正向传播，保存实例变量out