光伏发电量和用电量的概率预测研究综述（3）

前言
  由于本篇综述实在太长，故分为三部分，此乃第三部分。

1. 光伏发电量和用电量的概率预测研究综述（1）
2. 光伏发电量和用电量的概率预测研究综述（2）

4.3. Day-ahead

  PSPF中主要使用NWP模型进行提前一天或者更长时间的预测，然后运用统计后处理技术创建预测区间，but在PLF中并不使用物理模型。


  太阳能。为了将气象系统的惯性考虑在内，Golestaneh等人[115]意识到必须考虑时空依赖性，因为聚合尺度上的PV发电显示出时间和空间的强依赖性。因此，结合ECMWF提供的NWP模型的输出变量，研究了三个相邻PV站点的每小时分辨率的时间序列。首先作者应用QR来构建每个位置和交付周期的预测边际密度。为了模拟不同提前期的位置之间的依赖性，采用高斯copula，这是多变量分布的一种形式。然后可以使用copula来生成在特定位置和前置时间的未来发电的若干场景，即轨迹。各个区域的CRPS分数显示出明显的光伏发电，例如剖面，其中误差在中午或深夜最高，达到标称产量的9％至11％。通过PIT直方图评估了copula预测的可靠性，该直方图显示接近均匀分布，因此轨迹可以被认为与预测分布几乎相同。

  第一篇考虑非参数PSPF的论文，是由Bacher等人[91]撰写的。在他们的研究中，作者使用21个光伏系统的发电量来预测AR和带有外源输入（ARX）模型的AR提前36小时的发电量，其中NWP变量是后者的输入。由于上述模型受固定时间序列的约束，因此测量数据通过晴朗的天空发电量进行归一化，这是通过加权QR通过统计平滑找到的，而加权QR的权重由二维高斯平滑核确定。此外，RLS与用于光伏发电的自适应线性模型相结合可用于转换NWP预测，以便考虑条件的变化，例如面板上的污垢。此外，QR被用于构建几个分位数的预测密度，但不幸的是，没有使用概率度量来评估预测的效果。实际上，这在较早的研究中非常普遍，我们将在第5节中对此进行讨论。

  另一篇最早考虑PSPF的论文是由Lorenz等人[8]进行的研究。目的是根据ECMWF的NWP模型，以每小时的分辨率为德国南部的11个分散光伏系统提供概率预报。然而，由于时间和空间分辨率都太粗糙，因此引入了三种方法来提高分辨率。第一种方法包括空间平均和线性时间插值，这表明在晴朗天空中显着降低rRMSE。第二种方法基于用晴天天气辐照度替换ECMWF的预报，即晴天覆盖(tcc)低于0.03。最终方法基于消除预测和测量之间的系统偏差，其中偏差由依赖于天顶角和晴空指数的多项式函数建模，然后从N-WP预测中减去。通过使用PV站点的集合，作者清楚地表明随着区域尺寸的增加，集合的误差减小，尽管他们注意到增加站点的数量最终将导致饱和并且不会导致额外的误差减少。最后，通过假设预测误差的正态分布，以参数方式建立预测区间，其中标准偏差由依赖于天顶角和晴空指数的四阶多项式函数建模。此外，为了建立集合的预测间隔，将单个站点的标准偏差乘以误差减少因子。为了评估预测区间，考虑了相对标准误差，并且对于95%标称置信水平实现了91%的经验覆盖率。有人指出，这可能是因为在所有气象条件下误差减少因子保持不变。


  Almeida等[116]研究了西班牙北部5个光伏电站的QRF与非线性输入相结合的非参数概率预测的可能性。为了分别处理不同位置和不同连续WRF模型运行的WRF运行引起的空间和时间不确定性，作者对附近位置的预测进行了考虑。但是，没有描述连续运行中预测错误之间的联系。此外，还构建了三种不同的训练集，以评估哪种方法最有效。第一个训练集仅仅是前N天，而第二个训练集是根据要预测的天的清晰度指数与数据库中的天数之间的相似性构建的。最终的训练集基于预测的整个分布与数据库中的天数的相似性，并且发现该方法获得了最佳结果。此外，设计了多种情景来评估不同输入变量的相对影响，作者指出，包括预测和计算的辐照度数据可以产生更好的结果。更重要的是，他们得出结论，增加NWP变量的数量并不能保证提高准确性。最后一个有趣的结果是，只要时间序列超过15天，训练集的长度对性能没有实质性影响。遗憾的是，没有使用第2.5.2节中定义的概率度量。

  Alessandrini等人将基于NWP历史预报集的AnEn与QR和PeEn进行了比较，这三个地点代表了不同的气候区。由于这些方法已经在第3节中进行了全面的评估，我们将在这里立即讨论结果。作为第一个度量，三种方法的统计一致性通过秩直方图的手段进行比较，这是一种工具，以评估整体成员是否统计上相同的观察。AnEn显示了优于其他方法的性能，并产生了更可靠的预测密度。然而，令人惊讶的是QR的低扩散行为，表明没有足够的扩散预测。作者指出，这可能是由于优化过程，它设置遗忘因素相对较低，有利于CPRS。因此，QR在CRPS方面的平均表现较好，尽管有时它的表现不如AnEn和PeEn，主要是在太阳高程较低的时期。作者指出，这可能是由于过去的NWP预报与这些时期的发电量观测之间的相关性较低，AnEn处理这个问题更好，因为它只考虑过去的某些NWP预报，而不是全部

  Le Cadre等人[117]提出了一种ELM，用于为法国南部的一个地区构建30分钟分辨率的参数预测区间。通过使用来自该地区几个气象站的专家，并评估哪位专家提供的信息最有价值，作者可以对可能增加模型偏见的输入加以歧视。这是通过为该区域内的每一站引入一个损失函数来实现的，然后确定权重，以选择有价值的专家，即站，并抛弃过时的专家。他们发现，结合光伏发电的降水测量提供了最高的精度，PICP为0.916,PINAW为0.098，同时利用了该地区13个站点中的8个的数据。

  以与AnEn的做法相似，Yamazaki等人[118]提出了基于k-NN的每小时分辨率的预测区间估计，以便在数据库中查找类似的历史事件。这项研究是对[119]研究的改进。在邻居中，通过确定查询点和历史数据之间的欧几里德距离来选择k。然而，AnEn和这种方法的主要区别在于，预测密度是通过KDE估算的，而不是结合过去的预测来构建预测密度。利用高斯函数作为核来估计最能描述历史数据与当前观察之间的概率关系的密度函数。然而，由于核函数没有关于查询点和邻居之间的距离的任何信息，因此所呈现的设置显示出对最高分位数的显着偏差，并且因此权衡所有邻居等于构建预测密度。为了提高性能，作者通过三元组函数引入了加权核密度估计，该函数以非线性方式为邻居赋予权重。此外，还基于欧几里德距离调整高斯函数的标准偏差，从而为最近邻居分配较低的标准偏差。偏差显着降低，同时具有可靠性。遗憾的是，没有使用定量指标来评估预测间隔。

  与Yamazaki等人[118]的研究相似，FonsecaJr.等[87]利用欧几里德距离来识别前60天的每小时预测的输入数据与当前预测的输入数据之间的相似性。作者发现需要选择42小时来构建良好的预测区间。他们的方法基于支持向量回归（SVR），用于组织输入数据，结合计算的地外日照和网格点值预测与中尺度模型（GPV-MSM），其中预测小时的值并且后两者中的前一个用作输入。预测区间用高斯分布和拉普拉斯分布建模。作为基准，作者采用了一种不能被视为有效的非常规方法。它包括计算光伏系统的最大和最小功率输出，给定一小时的预测，然后这将提供100%的标称覆盖水平。显然，这些间隔的宽度将是如此之大以至于它们不实用，如作者所指出的那样，但如果所提出的方法将作为基准，则必须将其丢弃。结果表明，高斯分布倾向于低估低置信水平的预测误差覆盖率，并且拉普拉斯假设的误差分布与理想曲线更相似。作者没有根据PINAW量化预测间隔的宽度，而是将宽度标准化为PV系统的标称容量。他们发现，对于95%的置信水平，拉普拉斯分布和高斯分布的区间宽度分别为0.28和0.25。根据置信水平，发现PICP为97.1%至98.2%。

  作为GEFCom2014的参与者，Huang和Perry[120]用ECMWFN-WP数据预测了三个光伏电站的每小时发电量。由于时间分辨率是一小时，作者决定为辐照高于零的每小时创建一个模型。为了使数据去趋势，使用傅立叶变换使用低通滤波器对辐照度和功率时间序列的年周期进行建模。然后，通过为每个电厂和每个小时建立模型，使用GB来创建确定性预测。为了解释由电厂彼此相邻的事实引起的空间和时间相关性，将所有电厂的预测因子用作GB的输入。通过寻找类似的场景来应用k-NN来创建预测密度，其中k经验地设置为200.实现了令人满意的分位数分数0.0121，但重要的是要注意该模型花费13分钟完成256-核并行平台。


  Pierro等人[121]对使用ECMWF和WRF的NWP数据作为输入的几种数据驱动方法的行为进行了广泛而有趣的研究。目的是调查多模型集成（MME）在多大程度上可以胜过该集成的最佳表现成员。该集合的潜在成员是具有外因输入的季节性自回归综合移动平均值（SARIMAX），SVM和两个不同的MLP，其中一个使用了几个NWP变量（称为RHNN），另一个仅使用NWPGHI和温度，与晴朗的天空模型（GTNN）。MLP是使用[122]中描述的优化程序创建的，它有效地创建了一个能够胜过单个MLP的大型集合。作为第一步，上述模型分别用确定性度量进行评估，其中发现具有ECMWF输入的GTNN是表现优异的模型，技能得分为42.5%，如式（2.37）中所定义。此外，发现表现优异的模型使用ECMWF而不是WRF作为输入，即使这有时会导致偏差增加。发现性能最佳的MME是利用所有NWP输入数据的那个，即ECMWF和WRF，以及所有数据驱动的模型，与性能最佳的成员相比，其改善RMSE为6.3%。最重要的原因是它能够通过平均来降低单个预测变量的噪声。为了提供预测密度，假设正态分布并采用与Lorenz等人[8]类似的方法被用来评估这些。虽然没有使用定量测量来评估预测间隔，但可以看出这些是可靠的，尽管太宽，特别是对于低置信水平。一个有趣的结论是机器学习模型在NWP模型中纠正偏差的能力，因此，该性能并不总是与NWP模型的准确性相关。

  Sperati等人[89]应用ECMWF的集成预测系统（EPS）来提供0-72小时范围的概率预测。EPS通过在扰动的初始条件下运行模型几次来创建其整体，但是已知它是低分散的，这就是为什么需要应用后处理的原因。首先，采用NN来减少偏差并构建预测密度，然后应用和比较两种统计后处理技术。第一种方法估计导致EPS分散不足的方差不足（VD），而第二种方法，即EMOS，最小化整体数据集的CRPS。利用各种指标来评估绩效。用秩直方图评估统计一致性，尽管通过平滑直方图实现了对PeEn的改善，但是提出的具有VD和EMOS的模型仍然过于自信，即，它们显示缺乏扩散并且产生太窄的预测间隔。此外，以PeEn为参考的BSS表明，所提出的模型比PeEn表现更好，除了低太阳角度，即当预测和观测之间的相关性较小时，可能是由于阴影。在可靠性方面，两种方法都优于PeEn，而锐度稍微好一些。最后，两种方法在CRPS方面明显优于PeEn，当通过标称功率（NP）标准化时，两者均达到峰值8%至9%。

  Bracale等人[123]研究的主要焦点不是要创建最具竞争力的预测模型，而是提出新的基于成本的指数。这些指数旨在将预测的经济后果考虑在内。预测模型基于BI，有趣的是没有考虑NWP预测，而是将GHI和清晰度指数的估计平均值（分别由Beta和Gamma分布建模）与气象变量的测量值联系起来。关于基于成本的指标，作者提出通过将CRPS乘以$C_{E_t}/C_E^{max}$来扩展CRPS，其中$C_{E_t}$和$C_E^{max}$分别代表在t时刻的能量的经济价值和最大经济价值。他们认为，由于能源价格是可变的，预测的经济后果会有所不同，这对于“预测消费者”（例如公用事业）来说是很重要的。所选择的预报时间范围为上午07:00至下午8:00，整个研究期间保持不变。此外，作者通过互相关选择了最有影响的变量，以减少计算负担，并发现这些变量基于响应变量即太阳辐照度或清晰度指数在同一地点变化。基于成本的CRPS始终低于CRPS，根据其定义应该是这种情况。此外，基于清晰度指数的模型显示CRPS相对于持续性提高了25%，而基于太阳辐照度的模型实际上表现更差，与持久性相比，CRPS增加了52%。尽管作者没有详细说明为什么会出现这种情况，但可以解释为特定小时的CDF显示出更大的扩散，因此比基于清晰度指数的模型更不清晰。


  Davò等人[124]采取了不同的方法，旨在预测美国俄克拉荷马州的日常太阳辐照度。由于这种方法需要来自11个NWP集合成员的大量数据用于144个网格点和98个站点的每日辐照度测量，因此采用主成分分析（PCA）来减少变量的数量。PCA评估相关数据并查找观察到的变量的线性组合，然后将其转换为一组线性不相关的变量，根据它们的方差排序。作者继续表明，对于确定性（NN）和概率（AnEn） 情况，PCA显着减少了大约90%的计算时间。此外，NN和AnEn的确定性性能大大受益于PCA，而NN的性能略好于AnEn。不幸的是，NN没有被用于概率预测，例如，通过LUBE方法，因此仅评估了AnEn，但是看看确定性预测的结果是否可以转换为概率预测将是有趣的。尽管如此，AnEn与PCA结合使用证明是可靠的，同时产生了明显的预测间隔，尽管可靠性表明中位数周围的方差很大。此外，根据季节，最大观察到的辐射能量密度（MED）归一化的CRPS在0.03%和0.06%之间变化，其中春季由于可变性增加而显示出最高的CRPS。

  该研究由Zamo等人[52]完成,考虑了最长的预测范围，即66小时，结合日平均值的粗略时间分辨率。目的是评估由集合NWP数据提供的若干统计方法的性能和特征，以构建非参数预测密度。然而，不是直接使用集合NWP来提供密度，而是首先使用未受干扰的NWP成员训练QR和QRF模型，随后将其用于产生控制预测。然后，控制模型预测所有成员的分位数，之后为每个成员计算经验CDF。最后，对这些CDF进行平均，并从这些平均值中计算出分位数，以获得平均预测。结果表明，相对于基准，即气候学模型的改进范围为25％至50％。有趣的是，在总共八个基于QR的预测模型中，没有一个似乎始终比其他模型表现更好。此外，与本文讨论的先前研究类似，秩直方图显示校正后的预测分布不均，即没有显示出足够的传播。最后一个有趣的说明是，作者无法确定是否包括整体的所有成员都显着改善了预测性能。

  与Takeda[113]的研究相似，Saint-Drenan等[125]提出了一种通过概率方法估算区域光伏发电量的方法，虽然本研究没有进行概率预测，但有可能检索概率信息。这种方法的动机有两个：首先，作者强调使用NWP变量作为区域内一组参考光伏电站预测模型的输入是次优的，因为它没有利用NWP模型产生的所有信息。其次，当选择一组参考PV设备时可能发生错误，因此建议使用关于PV设备的参数的统计数据。为了找到这些参数，进行了灵敏度分析，其中在最小化所需信息量和最大化模型精度之间进行了折衷。结果发现，两个取向角最有价值。然后，为了估计这些参数的相对发生，使用具有35.000个PV植物的数据库，之后根据标称容量对植物进行分箱，因为发现容量和方向之间存在明确的关系。然后，这些相对出现将用作参数的联合概率分布，然后可以利用相对简单的PV功率模型来估计功率产生。结果显示该模型平均表现比公用事业差，平均高0.5％。然而，作者指出，他们并不打算减少预测误差，而是计算区域的总发电量，本案例研究用于验证模型。

  Chai等人[126]利用KDE和copula不仅预测特定的时间范围，而且还告知输出功率与所有中间时间范围的预测之间的相互依赖关系。上述方法背后的原因是预测误差与观测之间的相关性对总体不确定性具有一定的时间依赖性影响，应予以考虑。这里，copula用于建立KDE测量和预测之间的相互依赖关系。作为绩效指标，作者应用了区间分数，类似于Winkler分数，对锐度和可靠性进行了测试，尽管评估是以不可能用单个数量量化性能的方式进行的。

负荷
  刘等人[49]提出了一种有趣的方法，其中使用QR平均（QRA）将几个确定性预测整形为概率预测。确定性预测由所谓的姐妹模型创建，即具有相似结构但以不同时间滞后和不同训练数据长度运行的回归模型。此外，这些回归模型具有第2.4节中提到的新近效应。然后，应用QRA，其基于所有点预测最小化分位数q的分位数损失函数，以估计最佳参数集。使用了四种不同的训练数据长度，并使用滚动方案应用这些长度，这意味着更新了参数。在选择QRA模型的最佳组成时，作者表明，根据所使用的指标，即弹球，温克勒得分（50％）或温克勒得分（90％），QRA需要7或8个姐妹模型和183或365几天的校准数据。所提出的方法的显着优点在于它可以与许多点预测方法一起使用，在相同QRA模型中的不同方法与具有不同训练方案的单个方法一起使用。最好的QRA模型显示弹球得分为2.85，Winkler得分（50％）为25.04，Winkler得分（90％）为55.85。

  虽然研究（参见例如，[43]，[44]）已经提供了证据，假设表示错误的分布通常是无效的，或者至少是次优的，Xie等人[68]试图从另一个角度接近关于预测密度的假设。作者不是试图证明假设是否无效，而是试图通过假设高斯分布来提高概率预测的质量。本文中使用的回归模型是2.4节中描述的Vanilla模型。这些模型取决于温度，因此，为了创建预测密度，使用30年的历史数据来创建30个天气情景，这些情景又用于创建30个确定性预测，利用这些预测可以计算所需的分位数。结果表明，正态性假设确实无效，但是，当残差基于压延变量分组时，KS检验的合格率是显着的。然后，添加额外的模拟高斯残差来检查更高的通过率是否导致更好的分位数分数，这导致了有趣的结论。首先，如果基础模型的准确性较差，则此方法有助于改进预测，但如果基础模型显示出良好的准确性，则这可以忽略不计。其次，在KS测试和分位数分数之间没有发现趋势，这导致了更高的合格率并不表示更好的分组选项的结论。为了评估其结论的有效性，人工神经网络也被采用并显示出类似的结果[68]。

  Taieb等人[72]使用智能仪表数据在家庭层面上研究PLF的少数研究之一。预测方法基于增强附加QR，其在分位数的可加性假设下将加性QR与GB组合，即可以通过例如GB添加若干模型来估计每个分位数。在本文中，聚合和个人需求概况被认为是提前一天生成每小时的预测。除了考虑需求概况外，由于温度和电力消耗之间的高度相关性，还考虑了附近机场的温度曲线。此外，由于个人需求通常接近于零，作者进行了平方根变换以保证非零预测。结果表明，以一天中的时间为条件的基准，即考虑到日历变量，显示出比无条件基准显着改善，这导致确认这些变量的重要性。此外，对于增加的预测范围，该基准和QR在CRPS方面表现出类似的表现，这表明这些变量对于滞后的变量的重要性。最后，通过产生足够宽的预测密度来满足不稳定的需求，QR在分解规模上优于正常假设，超过了基准。然而，在汇总水平QR显示缺乏锐度。


  另一项考虑智能仪表数据的研究由Arora&&Taylor[53]执行，他们将非参数方法基于条件核密度（CKD）估计。然而，与Taieb等人[72]在智能电表数据预测中讨论的先前研究相反。由于潜在的有限可用性和可负担性，本作者未包括天气变量。结果发现，住宅消费者的需求模式在一周内没有显着变化，因此季节性因素被选择为每日和每周。为了考虑假期，将该日与前一个假日和上一个星期日进行比较，之后假期将被视为最相似的假期。关于CKD，它是KDE的扩展，作者估计变量$\hat{x}$的响应，以变量x为条件，有效地估计二维而不是一维的核。此外，已经提出了几种CKD结构，以确定最有效的结构，范围从以星期和一天的时间为条件到日内循环的类型。在这些方法中，有趣的是，实际上有四种基于CKD的方法和一种基于KDE的方法非常相似，后者基于考虑日内周期。发现CRPS介于0.013和0.055之间，最大的误差发生在易失时间段内。此外，该方法在预测时间为6小时的情况下也表现出最高的可靠性，而对于更长的交付周期，其他方法以及HWT基准也显示出非高的准确性。

  巴塔等人[127]旨在利用欧洲输电系统电力运营商网络（ENT-SO-E）的开放获取数据，建立国家能源消费预测框架。为了构建预测密度，采用了GB回归树（GBRT），并根据各国自己提供的实际负荷数据和预测进行了基准测试。拟议的框架从收集和存储数据开始，之后建立GRBT模型并用于预测。数据仅包含滞后值，并汇总为每小时值。就点预测而言，拟议的框架表现出良好的表现，尽管相对于现有方法的相对改进取决于该国，因为一些人本身使用非常准确的预测，例如斯堪的纳维亚和比荷卢三国。此外，作者认为很难比较实现这些结果的模型，因为这不是透明的，类似于使用了哪些数据。平均弹球损失为38.144，但由于各国只公布了点预测，因此无法将其置于背景中。

  Kou和Gao没有关注住宅用电量，而是提出了能源密集型企业（EIE）的PLF方法，特别是1000MW的钢铁厂。该方法基于高斯过程（GP），其假设方差是正态分布的。然而，由于假设高斯方差不被认为是现实的，作者应用异方差GP（HGP）进行本研究。此外，由于HGP的计算负担很大，作者对数据进行了细化，创建了简化的HGP（SHGP）模型。为了确定最有价值的数据作为回归模型的输入，作者采用了前贪婪的方法，将每个预测器分别合并并计算后续模型的预测误差，之后选择具有最低误差的组合并预测从候选集中删除。在可靠性方面，SHGP优于基准GP和样条QR（SQR），有趣地看到后一种方法一直低估每个分位数的需求。最后，SHGP模型的清晰度低于SQR，尽管不是很明显，使作者得出结论，所提出的模型是一种竞争性替代方案。


  另一种参数方法由Wijaya等人[128]采用，扩展了广义加性模型（GAM），它是响应变量线性地依赖于回归量的线性模型，扩展到GAM2，其中第二个GAM应用于平方残差。可以使用GARCH模型将该方法与平方残差建模进行比较，并且由于这些方法很少是同方差的，因此是必要的。首先，使用GAM函数估计平均值，随后将其用于预测，之后在与训练集进行比较时评估误差。然后在这些残差上安装另一个GAM。此外，在每天之后，通过用于添加模型的在线学习算法，向所提出的模型提供当天的数据，以便评估其错误并在必要时更新参数。在不添加在线学习算法的情况下，预测间隔没有覆盖整个置信水平，但是通过添加该算法可以实现。此外，作者表明预测间隔的宽度是令人满意的，尽管未使用2.5.2节中定义的宽度。此外，本文没有使用基准，因此阻碍了相对改进的比较。

  Quan等人的两篇论文[64]，[54]认为LUBE方法结合NN，在第3节中详细说明，用一周的时间来预测电力负荷。该方法的其他应用集中于最小化CWC，然而，作者认为，由于CWC具有许多参数并且对这些参数敏感，因此通过最小化宽度来解决优化问题可以更有效，同时限制覆盖概率。选择后者作为约束，因为这决定了预测区间的有效性[65]。为了解决优化问题，作者使用了PSO。此外，所提出的方法的性能对NN结构敏感，因此使用PINAW作为评估指标，已经构建了100个候选者，即两个隐藏层的10个神经元，并且对性能进行了测试。该模型显示多次运行的一致性，中位数PICP为90.81％至91.03％，中位PINAW为14.52％至36.53％，CWC为14.52％至36.53％，得分为86.59-4725.06，具体取决于每个城市的负荷变化。此外，它的表现优于基准模型ARIMA，ES和天真模型。最后，计算性能非常高，台式计算机上的预测间隔构建时间低于10毫秒。

  为了提高QR的预测准确性并允许其考虑非线性关系，He等人[129]提出基于KDE将NN与QR结合使用。由于QR是线性模型，并且回归量和回归之间的关系通过非线性依赖性更准确地建模，因此作者主张将NN与QR结合起来，如前所述。这意味着每个分位数由NN估计，之后分位数函数被用作KDE的输入以估计和平滑密度函数。尽管该方法是有趣的，但是所呈现的数值结果不允许基准（即，径向基函数QR（RBFQR））与所提出的方法之间的公平比较。更具体地说，根据案例研究，RBFQR的PICP为0％至5.95％，PINAW为1.06e-05％至1.24％。显然，接近零的PINAW与极低的PICP相结合，几乎没有传达关于响应变量概率的信息，因此，所提出的模型总是优于这样的基准。不幸的是，作者没有详细说明这些统计数据，特别是因为他们的方法显示了有希望的结果。


  作为考虑非线性关系的另一种尝试，He等人[130]提出利用基于核的SVR与QR结合，因为难以用后者解决非线性问题。通过引入基于内核的SVR，QR的损失函数可以用于优化问题而不是SVR的复数惩罚函数，然后将内核用作相似函数来逼近输入向量的非线性依赖性。最后，为了量化并考虑输入变量（即电价和电力负荷）之间的相关性，作者使用了copula理论。这项研究中有趣的前提确实是实时价格和电力负荷之间的相关性，这表明它具有显着的相互依赖性。培训数据的数量取决于提前期，即提前一天预测的培训数据的十天和提前4天预测的25天的培训数据。对于日前预测，结果显示所提出的模型在PICP和PINAW方面表现良好，PICP为100％，PINAW在15.76％和16.48％之间，具体取决于所选的内核函数。此外，当通过copula考虑实时电价时，PINAW显着降低至11.75％-11.62％。考虑到4天视野的案例研究显示，PICP减少，PINAW增加分别为82.81-96.35％和23.69-30.65％。此外，包含实时电价的改善并不像第一个案例研究那么重要。最后，作者指出，无论使用何种方法，都应包括实时价格。

  Xie和Hong[131]没有关注模型，而是比较了两个模型选择框架，特别是PLF。作者认为，PLF的模型选择可以通过点误差测量（第2.5.1节或概率误差测量（第2.5.2节））来完成，并且前者可以被认为是计算密集度较低但在应用于PLF。因此，作者研究了在使用概率误差测量时可以提高准确度的范围。作为模型，使用多元线性回归（MLR），其被馈送到多个温度场景以创建概率预测。使用的误差度量是确定性预测的MAPE和概率预的分位数分数。结果表明，后者的度量确实导致了比使用MAPE时更好的概率预测，但差异可以忽略不计。

  以下论文已根据GEFCom2014发表，并在此处以随机顺序进行讨论。首先，盖拉德等人[132]也利用GAM的扩展，即分位数GAM（quantGAM）参与并最终赢得GEFCom2014。首先，通过捕获均值和回归量之间的非线性关系，GAM用于拟合上述均值。然后，作为用于找到均值的最小化过程的结果的平滑函数被用作训练QR的回归量，以便获得每个分位数的估计。由于电力需求在很大程度上取决于一天中的时间，作者将时间序列分成24个，每天一个小时，因此，安装了24个不同的模型。此外，由于温度的影响及其不确定性，这些首先被分开了。这意味着首先预测取决于一年中的时间的温度，之后进行以温度为条件的负荷的预测。最后，后者对前者进行了平均，以获得最终的预测模型。该方法在比赛中获得第一名，弹球得分为3.98-10.73，具体取决于月份，夏季月份由于变异性较小而明显显示出更好的结果。此外，虽然未指定哪个模型被用作基准，但是在基准测试中实现了显着的改进。

  谢和洪[133]提出了一个PLF框架，其中进行了预处理，预测和后处理。通过使用Vanilla基准模型清理数据来初始化预处理步骤。这是通过用所有可用数据训练模型并随后计算观察和预测之间的绝对百分比误差（APE）来完成的。如果误差大于50％，则该观察将被预测所取代，这是0.05％的数据的情况。预处理的第二部分涉及气象站选择，即哪个匿名气象站将提供最有价值的信息。第一次预测是通过多元线性回归（MLR），即Vanilla基准进行的，之后残差预测是四种方法的平均值，即未观察到的组分模型（UCM），ES，ANN和ARIMA。最终的预测是第一次预测和平均预测的结合。后处理基于Xie等人[68]的论文，其中发现残差的正态性假设可以改善概率预测，因此这里应用了这种方法。结果显示，残差的后处理导致分位数分数方面的改善，有趣的是，在该类别中，平均而言，基准实际上以7.908的分位数得分实际上表现最佳，因此优于模型。结合基准和前面提到的四种模型。不幸的是，作者没有提到为什么会这样。


  Mangalova和Shesterneva[134]采用了非参数方法，拟合了一系列Nadaraya-Watson估计器。为了对基本模型进行优化，作者通过最小化分位数来寻找核的最优带宽。为进一步改进所提出的模型，虽然预测结果并无显著改善，但仍以温度作为输入变量。分位数得分在3.93到12.74之间，视月份而定。在夏季的几个月里，变化较少，分位数得分平均较低。该模型的主要优点是可以获得仅依赖于一个参数的预测密度。最后，作者得出结论，在比赛后对转换为分位数的方法进行修改，可以显著提高准确性。

  Dordonnat等人[135]使用了GAM温度依赖的确定性负荷模型，基于广义交叉验证(GCV)评分选择了匿名气象站。然后，针对温度偏离移动平均的情况建立AR模型，生成N个样本，然后插入确定性负荷模型，获得N个负荷样本。最后，将确定性负荷模型预测样本与观测样本进行比较，评估误差，量化不确定性，并推导出其分位数。作者指出，MAPE最高的模型，即确定性度量，并不意味着它在用分位数分数评估时表现最好，这是一个明确的信号，表明绩效度量不能互换。表现最好的模型的平均分位数得分为7.37，这个分数确保了Dordonnat等人进入竞赛的前五名。

  Ziel和Liu[136]提出了一种基于最小绝对收缩和选择算子（套索）估计的方法。选择了以负荷和温度为输入的VAR模型，并扩展了代表分段线性函数的阈值。这样做的原因是负载与温度之间的非线性关系。但是，为了减少潜在阈值函数的数量并因此减少了计算时间，应用了套索算法，该算法仅选择了显着的非线性影响。由于预测范围是一个小时且具有每小时的分辨率，因此考虑了之前的1200个时滞，即1200小时。此外，选择了八个随时间变化的系数，从而反映了与季节有关的最重要的系数，并尽可能减少了参数空间。相反，作者认为残差是同方的，这一假设在PLF中很少成立。拟议的模型在分位数方面优于Vanilla基准，在竞争中平均为7.44。


  Haben和Giasemidis[137]根据GEFCom2014发表了关于PLF的最终论文，我们将其纳入我们的综述。作者以Arora和Taylor[53]的工作为基础，建立了一个温度范围。但是，此处使用的衰减参数是对称的，这意味着将一年中的相似日期纳入预测。此外，QR还参与创建混合模型以通过添加这些模型来确定相对改进。结果发现，以温度为条件的CKD对于日间预报的效果最佳，但对于较长的视野效果较差，这是由于温度预测不准确所致。此外，将不同的CKD与QR结合使用，得出的结论是QR带来了这些组合中所见的大部分改进，并且被认为是平均而言最佳的非混合预测。不幸的是，没有给出平均分位数，但是从给出的图表中估计得出的分数约为8。

  Takeda等[138]将EnKF与SSMs相结合，对东京及其周边地区的电力负荷进行了预测和分析。值得注意的是，作者并没有进行概率预测，但主要作者后来研究了EnKF在光伏发电的情况下，并在其中实际上进行了PSPF[113]。作者认为，将SSMs与EnKF结合使用的主要原因是，统计方法，如ann或MLR，不能提供任何关于电力消耗结构变化的洞见。为了进一步提高精度，作者采用了lasso和MLR。由于使用lasso和MLR的结果没有显着差异，他们建议使用lasso，因为它有避免过拟合的能力。在MAPE方面，EnKF+lasso模型获得了1.87%的分数，虽然它优于目前使用的MLR模型，但它没有优于第二个MLR模型的实用程序。

4.4. Comparison between PSPF and PLF

  表1概述了在前面章节中已经讨论过的论文。它的目的是提供与概率预测相结合的最重要的方面的概述。此外，图2和图3给出了在已综述的文章中所采用的方法以及考虑的提前时间的概述。从图2可以清楚地看出，回归方法是PSPF和PLF最常用的方法。更具体地说，在PSPF的情况下，25%的论文采用物理或混合物理方法，这是相对较少的数量。其主要原因也可以从图3中推断出来，从图3中可以看出，大多数研究人员调查日内和小时内，其中统计方法是首选的。此外，统计方法也已用于日前预测。对于PLF，由于回归方法简单，并且PLF通常考虑聚合需求，这意味着时间序列比单个需求的情况下更平滑，因此更优选回归方法。由此得出结论，如果分辨率和范围相同，PSPF和PLF可以结合起来进行净需求预测。可以做出的另一个观察是，在PLF情况下提前时间更长，这主要是因为所综述的方法考虑了日历变量，即利用了电力需求的高度重复特性。

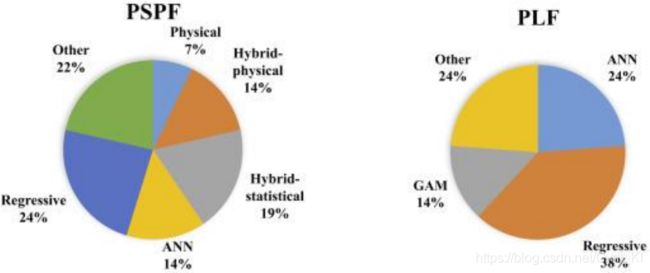
       图 2. 综述的研究中预测技术概览

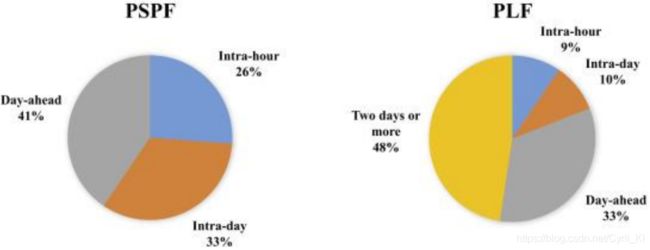
       图 3. 综述的研究中提前时间的概览


  PSPF和PLF之间数据需求的差异程度取决于所使用的方法和可利用的输入数据之间的相关性。例如，文献研究表明，温度和电力需求之间存在显著的相关性，这在PLF情况下经常被利用，如表1所示。虽然温度和辐照度之间也有相关性，但相关性不明显，因此，为了减少输入变量的数量，这种关系通常被忽略，而其他变量，例如降水，可能被认为更有价值。然而，如果利用一种结合相关变量的既适合PSPF又适合PLF的方法，则可以通过净需求预测同时预测两者。此外，在2.5.2节中定义的性能评估允许PSPF和PLF之间的直接比较。虽然在分离PSPF和PLF的情况下通常不需要这样做，但是由于变异性的差异和随后的预测精度的差异，评估和比较这一点是有用的。

  从图4可以看出，非参数方法在PSPF和PLF中都占主导地位。然而，正态分布的假设仍然很重要，这通常与自回归方法（如AR或ARIMA模型，或物理模型）结合使用。自回归方法假定正常性的原因是这些方法固有的，因为误差应该是正态分布的。值得注意的是，最近的论文一般不作关于分布的假设，而是采用非参数方法。因此，如果一个人在较长的时间尺度上研究概率预测的论文，那么这些论文中很大一部分会采用参数方法。本质上，这种发展是合乎需要的，因为分布假设一般不合适[43]，[44]。

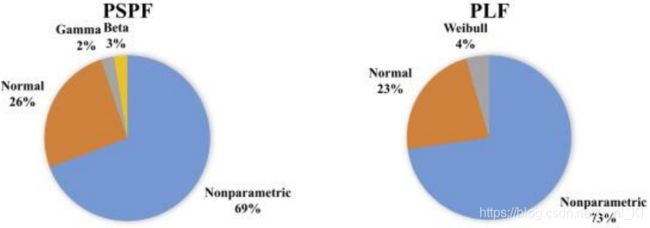
       图 4. 综述的研究中假设分布的概述

  智能电表渗透率的提高使研究人员能够提高时间分辨率，从图5结合表1可以看出，这是一个相当近期的趋势。大部分论文仍集中在小时分辨率上，这对于日间市场而言是令人满意的，但对于日趋重要的日内市场而言却是粗糙的。在这个市场中，必须平衡发电量和需求量的短期波动，以维持系统的效率和安全性，而当时间分辨率太粗糙时，则无法控制这些波动。显然，如果将PSPF和PLF结合到净需求预测中，则在其上训练统计模型的数据的分辨率应相同。

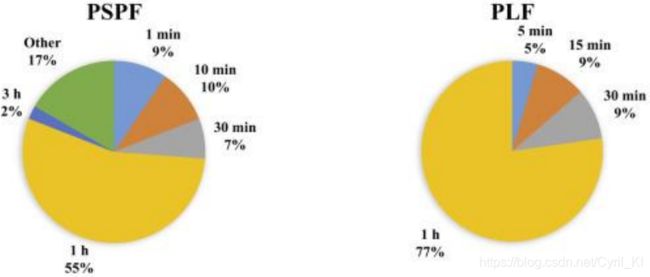
       图 5. 综述的研究中时间分辨率的概览


  图6指出了PSPF和PLF在空间分辨率方面的异同。如综述所示，大多数关于PLF的论文考虑的是总电耗，例如，市镇规模。而大多数关于PSPF的研究集中在单个地点或发电厂。虽然预测个人负荷数据是更具挑战性的，但这样做的研究设法取得了良好的效果。因此，空间分辨率之间的这种差异为将来有趣地研究净需求预测铺平了道路，其中可以利用平滑效应来降低城市尺度上PSPF的平均预测误差，同时利用PLF减少的电力消耗变异性。相反，也可以考虑自下而上的方法，其中选择一组代表性的建筑物并用于预测生产和消费。的确，研究表明自下而上的方法可以提高MAE的准确度3%[52]，因此需要更多的研究来创建关于如何为光伏电站和电力消费者选择代表性站点组的范例。有了这样的范例，可以显著减少所需的数据量，同时保持高精度。

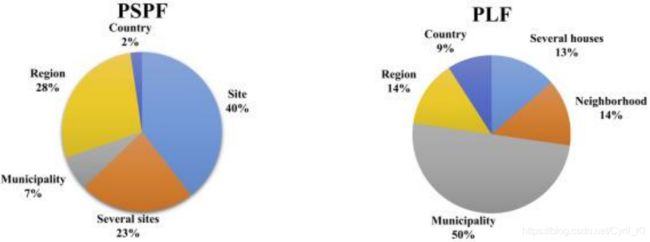
       图 6. 综述的研究中空间分辨率的概览

5. Discussion

  因为启动和关闭时间长，以及大量的斜坡限制，所以传统发电机进行提前计划是有必要的。此外，由于电力市场不断变化，例如使用智能电表、部署表后DG以及增加电动汽车的数量，为了平衡随机生产和消费，日内和时间内预测也可能变得越来越重要。作者认为有必要对高时间分辨率进行更多的研究，特别是在光伏在建筑环境中的高渗透，伴随着太阳变化和日益复杂的电力消费模式，如D2R，以及随后电网所经历的复杂网络需求这种情况下。

  此外，由于气象条件的惯性，PV电力生产数据的广泛可用性提供了另一机会，即发现例如城市规模的时空相关性。与其使用昂贵的天空成像摄像机，不如尝试使用PV系统及其地理位置来发现上述情况下的短期趋势并提高预测的准确性。另一种有希望的方法可能是使用例如copula来建模辐照度和PV功率的时空相关性，以预测时空。此外，本评论中发现的PSPF和PLF之间的空间分辨率差异为研究在不同空间范围（例如，城市或邻里级别）上的净需求预测的可能性提供了机会。

  在整个文献研究中，有几点值得注意：

1. 概率度量在PLF和PSPF中均未得到一致应用。
2. 在CRPS情况下对结果进行归一化有时是利用PV设备的额定容量，有时是利用最大的实测产量。作者给出的建议是同时使用这两种方法，因为前一种方法具有透明度，而后一种方法则可以考虑季节变化。
3. 对概率预测而言，标准化是必须的。
   
     
4. 已经多次证明，在概率预测中假设密度很可能会给出对未来的不准确估计。
5. 此外，假设固定密度的另一个缺点是，最终的模型不太通用，也就是说，不能应用在每个位置，因为这可能产生不同的误差，不能用先前假设的密度来描述。
6. 没有一种单一的最佳方法可以适用于任何地点和任何情况。
   
   

  重点要强调以下论文：

1. Bilionis等人[102]结合递归GP利用卫星图像，这两种方法似乎并不经常使用，但都产生了有希望的结果，特别是因为卫星数据的分辨率不断提高。
2. Quan等人[54]采用了下界估计(lower upper bound estimate, LUBE)方法[79]进行训练人工神经网络(ANN)预测区间而不是点预测。诸如LUBE方法的建议很有价值，因为它们为继续使用神经网络进行概率预测铺平了道路，同时认识到用诸如RMSE之类的确定性度量训练神经网络是次优的。相对较少的研究利用了气象过程的惯性，例如，[106]，[96]，[115]。
3. Pierro等人创建了一个由数种数据驱动的方法组成的集合[121]，并显示了在结合具有类似精度的预测时，在技能得分方面具有显著的潜力。
4. Taieb等人[72]利用智能电表数据在细分水平上预测电力消耗，并指出，当时只有两篇类似的论文存在。一个重要发现是，尽管此空间分辨率的可变性增加，但是一天中的时间仍然是很好的解释变量。
5. Torregrossa等人进行的研究[90]首次设计了一种方法，可用于任何预测模型，可以在秒至分钟分辨率上创建预测区间。当光伏系统在建筑环境中的渗透增加，更严格的电力控制变得必要，以保护那些连接到它的人免受重大的电力变化时，这将变得更加重要。
   
   

  如果预测的PV发电量比测量的要高，则必须考虑额外的成本，例如快速响应发电机的启动成本。Bracale等人提出了基于成本来量化误差的方法。[123]，但是需要更多的研究来解决这个问题。

  很多模型难以对特定的情况进行一个好的预测。一般情况下都是为模型提供大量的数据，从而避免了在训练集上进行测试。

6. Conclusion

  总结：本文干了以下几件事：

1. 对PSPF和PLF的性能指标、方法和最新进展进行了广泛概述。这占据了本文的绝大部分篇幅。
2. 确定了在该领域的研究空白，比如解决净需求预测概率性能指标的影响。
3. 找到了PSPF和PLF之间的共同点，从而能够进行净需求预测。即二者在空间和时间分辨率方面存在重叠，但在可变性方面的相似性似乎可以显著不同，这为提出新方法提供了可能性。
4. 讨论了标准化在性能度量和数据预处理等方面的重要性。

Acknowledgments

  这项工作由智能电网ERA-NETCofund在“增加虚拟网络中电动车充电光伏发电自耗”项目以及SamspEL2016-2020在“太阳能发电预测模型的开发和评估”项目资助。此外，作者要感谢匿名审稿人，有助于提高本文的质量。

原文链接：Review on probabilistic forecasting of photovoltaic power production and electricity consumption