numpy常见方法使用

python基础内容（点击查看）
numpy生成数组方法
（以下内容均是个人理解，如有偏差，请多多指教）

常见方法（查表）

含义	具体使用
转置	数组名. T
上下合并	np.r_(上数组，下数组)
左右合并	np.c_(左数组，右数组)
变换维度（经常用到）	np.reshape((新行数，新列数) , order="c"或其他） 经过该方法之后产生的是一个新的数组，原数组没有发生变化
在给定的步长产生的数组（经常用到）	np.arange(起点(可有可无)，终点，步长(可有可无)，dtype=输出数组的类型)
条件函数	np.where(筛选条件，被筛选对象，不满足条件的填充方式)

返回索引值	具体使用
返回非零数的索引	np.nonzero(数组 或者 矩阵)
返回最大值索引	np格式变量名.argmax()
返回最小值索引	np格式变量名.argmin()

数组或矩阵是否为空	具体使用方法
序列至少 存在判断	np格式变量名.any()
序列全部 存在判断	np格式变量名.all()

积累 运算	具体使用
累加运算	np格式变量名.cumsum()
累乘运算	np格式变量名.comprod()
和前一个元素做差	np.diff(np格式变量名)

最常用到的

统计函数	具体使用方法
求最大值	np格式变量名.max() 或者： np.max(np格式变量名)
求最小值	np格式变量名.min() 或者： np.min(np格式变量名)
求平均值	np格式变量名.mean() 或者： np.mean(np格式变量名)
求中位数	np格式变量名.median() 或者： np.median(np格式变量名)
求标准差	np格式变量名.std() 或者： np.std(np格式变量名)
求方差	np格式变量名.var() 或者： np.var(np格式变量名)
求和	np格式变量名.sum() 或者： np.sum(np格式变量名)
求分位数	np.quantile(np格式变量名, 分位数数值设定)

以上对于含有缺失值的数组，它们返回的结果也是缺失值，如果需要略过缺失值，必须使用 nan 类型的函数*，上述的几个统计函数都有对应的 nan* 函数。
比如： np.nanmean()
其他的统计函数具有类似属性

相关性的量化	具体使用
协方差	np.cov(np格式变量名1， np格式变量名2)
相关系数	np.corrcoef(np格式变量名1, np格式变量名2)

在 numpy 中

轴线方向	代表含义
axis = 0	结果为列的统计指标
axis = 1	结果为行的统计指标

import numpy as np
target = np.arange(1, 10).reshape(3, -1)
print(target)
print(target.sum(axis=0))

# print(target) 结果：
#[[1 2 3]
# [4 5 6]
# [7 8 9]]
# print(target.sum(axis=0))  结果：
# [12 15 18]
# 解释： axis 结果是按列进行计算的 即  1 + 4 + 7 = 12， 同理可得其他输出

广播机制

广播 = 广而告之，进行传播。不怕新闻小，就怕别人不知道。传播的前提是：彼此之间有共同的媒介（常见的是 语言）。
所以python 中的广播是，将两个不同维度的变量之间自动扩充形状，完成计算。

标量和数组

import numpy as np
target = np.arange(1, 10).reshape(3, -1)
res = 3 * target + 1
print(res)

#解释： 
3*target = 标量  * 数组 ，这里就是完成一次广播，
3*target + 1 （加1操作：完成了第二次广播）

二维数组之间的操作

数组元素要一致才能进行对应元素操作。其中广播的方式是使一些数组进行自动扩充（并不是所有都行，是有条件的）

import numpy as np
a = np.array([[1, 2, 3],
              [4, 5, 6]])
b = np.array([[3, 2, 1],
             [6, 5, 4]])
result = a * b
print(result)

基本运算

向量内积

dot

先把数组变成向量，原数组 = np格式变量名.reshape(-1)
向量1.dot(向量2)

import numpy as np
a = np.array([[1, 2, 3],
                [4, 5, 6]])
b = np.array([[3, 2, 1],
             [6, 5, 4]])
a = a.reshape(-1)
b = b.reshape(-1)
res = a.dot(b)
print(res)

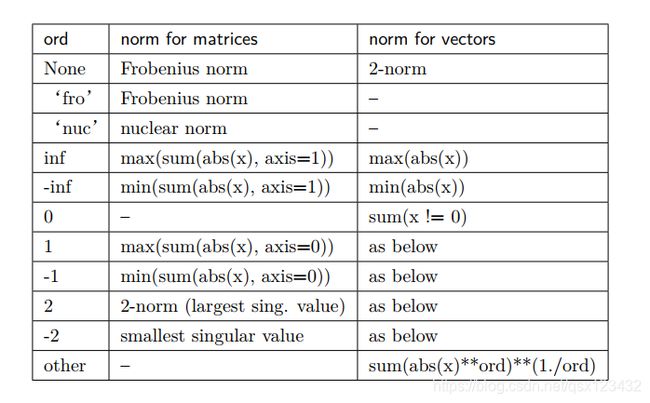
向量范数和矩阵范数

np.linalg.norm(np格式变量名， …… )
省略号代表：下面表格中的内容。

矩阵乘法

矩阵1@ 矩阵2
（注意：要保证可以满足矩阵相乘的规则）

import numpy as np

a = np.array([[1, 2, 3], 
                [4, 5, 6]])
b = np.array([[3, 2, 1],
             [6, 5, 4]])
b = b.reshape((3, 2), order="c")  # 使乘法能够进行，满足规则
result = a @ b
print(result)