联邦学习中的non-iid总结

最近研究联邦学习（federated learning，FL）中的non-iid的解决办法时遇到瓶颈，写成博客将最近的工作总结一下，希望有大佬看到这篇博客不吝赐教。

什么是non-iid

先从维基百科引出独立同分布的定义：

在概率论与统计学中，独立同分布（英语：Independent and identically distributed，缩写为IID）是指一组随机变量中每个变量的概率分布都相同，且这些随机变量互相独立。

一组随机变量独立同分布并不意味着它们的样本空间中每个事件发生概率都相同。例如，投掷非均匀骰子得到的结果序列是独立同分布的，但掷出每个面朝上的概率并不相同。

那么non-iid的意思即变量之间非独立，或者非同分布。

• 非独立：对象之间存在关系。例如以某人的行为为随机变量，在某时刻观测到行为behavior1，某时刻观测到行为behavior2，这两个行为之间可能有某种联系。例如一个人走在路上，淋雨了（behavior1），撑开伞（behavior2），它们之间有时序关系。
• 非同分布：两次观测的概率分布相同。例如某变量服从均匀分布，我们进行了一次观测；过一会服从正态分布，我们又进行了一次观测。这两次观测的变量就是非同分布

什么是FL中的non-iid

在联邦学习中，non-iid的意思一般是值不符合同分布的情况，因为数据的分布肯定是独立的，但是它们不一定服从同一采样方法。例如全集中有100类图片，某设备中都是风景类图片，某设备中都是人物类及植物类图片，前者是一种分布（1/100），后者是另一种分布（2/100）。反之，如果某设备中有这100类图片，其他设备中也有这100类图片，那么它们就是同分布的。看看下面的例子：

where we first sort the data by digit label, divide it into 200 shards of size 300, and assign each of 100 clients 2 shards. This is a pathological non-IID partition of the data, as most clients will only have examples of two digits. [1]

The training data are non-iid, that is, a device’s local data cannot be regarded as samples drawn from the overall distribution. The data available locally fail to represent the overall distribution. [2]

For the non-IID setting, each device still owns 600 samples, yet 80% of which come from a dominant class and the remaining 20% belong to other classes. For example, a “0”-dominated device has 480 data samples with the label “0”, while the remaining 120 data samples have labels evenly distributed among “1” to “9”[3]

For non-IID setting, the data is sorted by class and divided to create two extreme cases: (a) 1-class non-IID, where each client receives data partition from only a single class, and (b) 2-class non-IID, where the sorted data is divided into 20 partitions and each client is randomly assigned 2 partitions from 2 classes[4]

Non-identical client distributions:[5]

• Feature distribution skew (covariate shift):同一类别，有不同的表现形式，如同样的数字，不同人的写法不一样
• Label distribution skew (prior probability shift)：同样的标签，有不同的表现形式，
• Same label, different features (concept shift):
• Same features, different label (concept shift)
• Quantity skew or unbalanced:

可以发现它们的共同点：每个设备中的数据分布不能代表全局数据分布，即每个设备中类别是不完备的。可以任意设定哪些比例的设备拥有哪些比例类别的样本。例如10分类问题中，5%的设备有3类样本，10%的设备有5类样本，30%的设备有10类样本……哪些比例的设备、哪些比例的样本类别都是可以改变的参数，从而决定了non-iid的程度。此外，每个类别样本的数量也会影响non-iid程度，但数量上的不同一般描述为unbalanced。

如何衡量non-iid的程度

[2]给出了non-iid的一个评价方法，即全局目标函数的最小值与本地目标函数最小值之和。设想non-iid程度最小，即每个设备中分布都一样，那么本地目标函数最小值的加权和就是全局目标函数的最小值。现在由于non-iid从中作梗，每个本地目标函数优化方向都出了偏差，最小值是最适合本地那两类数据的（如手写数字1和2），它们加权平均在一起，不等于全局目标函数的最小值。

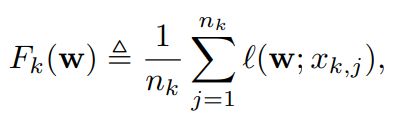
下图是异构程度的量化：

解释：
$$F^{\ast }=\sum _{\mathrm{k}=1}^N{p}_k{F}_k(w^{\ast })$$
那么
$$\Gamma =\sum _{\mathrm{k}=1}^N{p}_k{F}_k(w^{\ast })-\sum _{\mathrm{k}=1}^N{p}_k{F_k}^{\ast }$$
即使用一个参数的全局模型的目标函数与使用n个参数的本地模型的目标函数之和 的差。

non-iid带来的问题

降低模型表现[4]：
the accuracy of convolutional neural networks trained with F edAvg algorithm can
reduce significantly, up to 11% for MNIST, 51% for CIFAR-10 and 55% for keyword spotting (KWS)datasets, with highly skewed non-IID data.如下图红线所示。

证明FedAvg在non-iid情况下收敛

[2]证明了部分设备参与、全部设备参与情况下的收敛性。其中定理3说明要达到指定的准确率ε，需要通信的轮数T/E等于

还有一些参数的定义请参考原文。这个公式告诉我们，non-iid也是能收敛的，要减少通信轮数，可以从哪些变量入手：

1. E
   E太小意味着系统轮次（通信次数）大，造成通信负担；E太大意味着系统较低的收敛率。需要调整E，在通信效率和收敛速度之间做一个权衡
2. K
   一个足够大的K是必要的，能加速收敛。但是无须在每轮训练中将K设置得尽可能大（如接近N）
3. η
   为了抵消本地训练中E步的SGD带来的bias，学习率η必须递减，否则即使是在全部梯度下降中，收敛率也会变成Ω（η），不一定能收敛到最优值

这篇文章的证明过程非常详尽，我只看懂了部分，后面有兴趣再研究。

如何缓解non-iid带来的挑战

---

引用

[1] McMahan B, Moore E, Ramage D, et al. Communication-efficient learning of deep networks from decentralized data[C]//Artificial Intelligence and Statistics. PMLR, 2017: 1273-1282.
[2] Li X, Huang K, Yang W, et al. On the convergence of fedavg on non-iid data[J]. arXiv preprint arXiv:1907.02189, 2019.
[3] Wang H, Kaplan Z, Niu D, et al. Optimizing Federated Learning on Non-IID Data with Reinforcement Learning[C]//IEEE INFOCOM 2020-IEEE Conference on Computer Communications. IEEE, 2020: 1698-1707.
[4] Zhao Y, Li M, Lai L, et al. Federated learning with non-iid data[J]. arXiv preprint arXiv:1806.00582, 2018.
[5] Kairouz P, McMahan H B, Avent B, et al. Advances and open problems in federated learning[J]. arXiv preprint arXiv:1912.04977, 2019.