DJL 教程 2.2 神经元的概念及应用
前面我们提到,人工智能决策系统类似一个函数,那这个函数是如何来解决形形色色的问题的呢?
在回答这个问题之前我们先来看看人类是如何决策的
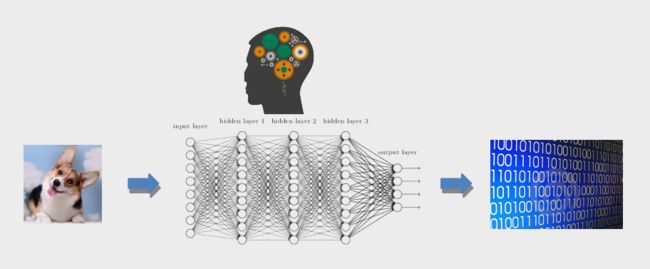
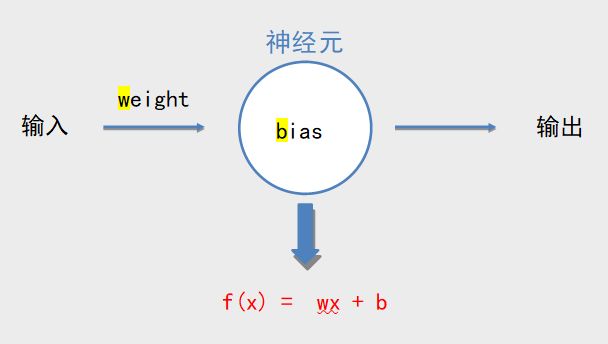
当我们看见这张图的时候我们能知道图片中是一只狗,那我们是如何知道这是一只狗呢?研究发现当光线进入我们眼睛的时候就完成了输入,我们眼睛中的视觉细胞会接收到信号后会传递给附近的神经元,神经元进行简单处理后继续传递给下一个神经元,最终传递到我们的大脑,我们的大脑中神经元的个数更多,结构更复杂,经过这些神经元的处理后我们知道了这张图片是一只狗狗.进一步研究发现,大脑的决策过程虽然复杂,但都是由结构相对简单的众多神经元完成的,而每个神经元做的事情相对简单.于是人们开始用计算机模拟神经元的处理过程,其中f(x) = wx + b的处理过程被绝大多数AI引擎采用.没错看错,这个方程要用到高中的知识,并且我会尽量把本课程的难度控制在高中知识范围内,毕竟不是每个人都在大学认真学习过.
当然只用这个直线方程来模拟神经元还是不够理想,于是引入了激活函数来提高性能,激活函数将在后面章节讨论.
接下来我们通过一个飞机投弹的案例来理解神经元是如何来解决实际问题的.
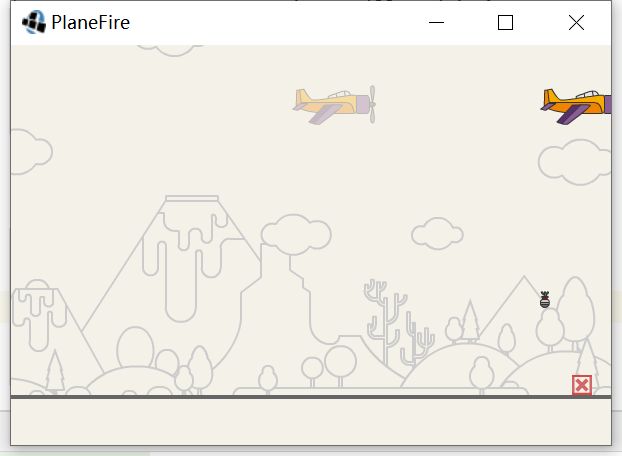
在使用神经元之前先通过已有的知识来解决问题
1,观察并总结规律
- 目标出现位置 x = 475
- 投弹点 location = 195.0
- 目标出现位置 x = 360
- 投弹点 location = 80.0
- 目标出现位置 x = 323
- 投弹点 location = 43.0
- 目标出现位置 x = 501
- 投弹点 location = 221.0
- 目标出现位置 x = 591
- 投弹点 location = 311.0
- 目标出现位置 x = 473
- 投弹点 location = 193.0
- 目标出现位置 x = 466
- 投弹点 location = 186.0
- 目标出现位置 x = 561
- 投弹点 location = 281.0
- 目标出现位置 x = 573
- 投弹点 location = 293.0
- 目标出现位置 x = 566
- 投弹点 location = 286.0
2.总结规律
设:
飞行高度=h
重力加速度=g
下落时间=t => 1/2 * g * t * t = h
飞机数度=v
目标位置=x
投弹位置=y => v * t = x - y
约t => y = x - v * Math.sqrt(2 * h / g)
令常量b = v * Math.sqrt(2 * h / g) => y = x - b
取数据
* 目标出现位置 x = 475
* 投弹点 location = 195.0
* 目标出现位置 x = 360
* 投弹点 location = 80.0
得到b = 280 => y = x - 280
private static int calc(int x) {
return x - 280;
}
3.验证
public static void main(String[] args) {
PlaneFire.lv1Ready(x -> {
int location = ai(x);
PlaneFire.fireLv1(x, location);
});
}
复习高中知识
使用神经元的知识的原理来解决这个问题
神经元只会解f(x) = wx + b方程我们前面介绍过,所以我们可以这样
y = x - 280 => f(x) = x - 280 => w = 1,b = -280
代码实现
public static void main(String[] args) {
PlaneFire.lv1Ready(x -> {
int location = ai(x);
PlaneFire.fireLv1(x, location);
});
}
//AI
private static int ai(int x){
int w = 1;
int b = -280;
return neuron(x,w,b);
}
//神经元
private static int neuron(int x,int w,int b){
return w * x - b;
}
参考工具:https://nihe.91maths.com/linear.php