R-交通事故数据分析报告

引言

该数据来源于kaggle网站中的一个项目，其原数据集（US_Accidents_Dec20）是一个数据量49列，共400多万数据量包含2016-2020年交通事故信息。
本文的目标是对这些数据进行统计分析，探寻发生事故最多的州，并探查什么时候容易发生事故，事故发生时天气状况，并对此做出可视化展示：总结分析所得信息，讲述美国发生事故的总体情况，找出影响事故发生以及影响事故严重程度的因子；最后对事故的严重程度进行预测分析。

数据基本分析

缺失值处理

查看原始数据的缺失值数量结果如下：

library('dplyr')
library('DMwR')
library('ggplot2')
library('lubridate')
#install.packages('Rmisc')
library(Rmisc)
library(mice)
#install.packages('VIM')
library(VIM)
library(zoo)
library(reshape2)
#导入数据
data = read.csv("D:/R数据/US_Accidents_Dec20.csv")
####----------------数据预处理-----------------------
head(data)
#查看数据的变量名
colnames(data) 
#查看数据的结构（4232541，49）
dim(data)
#查看数据中含有空值的列
colSums(is.na(data))
table(is.na(data))
#可以看到TMC含1516064；End_Lat含2716477；End_Lng含2716477
#Number含2687849；Temperature.F.89900；Wind_Chill.F.1896001；
#Humidity...95467；Pressure.in.76384；Visibility.mi.98668；
#列变量可视化展示
miscol = colSums(is.na(data))##列变量缺失值计数
miscol = sort(miscol,decreasing = T)  ##降序排列
miscol = miscol[miscol > 0]
p <- barplot(miscol,col = 'pink',axisnames=F,ylim=c(0,2000000),main = '列变量缺失值数量展示')
axis(side=1,p,labels = F)
labs <- names(miscol)
text(cex=0.8,x=p-0.25,y=-0.1,labs,xpd=T,srt=45,adj = c(1,1))

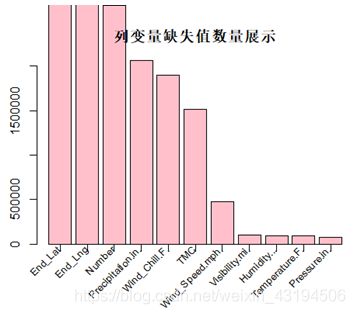
首先，本文将变量值缺失个数多于总个数的20%的交通事故案例去除，此处共去除22913个案例；而后，因街道编号、风寒指数、风速、降水量的缺失值过多，所以将这几个变量移除；然后，移除与事故发生原因不相关变量；最后，采用均值插补的方法对温度、湿度、气压和能见度四个变量的缺失值进行插补，最终保留了27个变量。

#去除空值占比过大的行
r1 <- rowSums(is.na(data))/ncol(data) >= 0.2
#r1是缺失值大于0.2的行
data1 <- data[!r1, ]
rm(r1)
colSums(is.na(data1))
dim(data1)    #4209628      
#将空值过多以及对研究影响因素作用不大的变量去除
data2 <- subset(data1, select = -c(ID,Source,TMC,End_Time,Zipcode,Timezone,
                                   End_Lat,End_Lng,Number,
                                   Distance.mi.,Description,Airport_Code,
                                   Weather_Timestamp,Wind_Chill.F.,
                                   Civil_Twilight,Nautical_Twilight,
                                   Astronomical_Twilight))

#补齐缺失值
##用均值插补温度湿度气压能见度
fun1 <- function(x) {
  x[is.na(x)] <- mean(x, na.rm = TRUE)
}
data2$Temperature.F. <- sapply(data2$Temperature.F., fun1)
data2$Humidity... <- sapply(data2$Humidity..., fun1)
data2$Pressure.in. <- sapply(data2$Pressure.in., fun1)
data2$Visibility.mi. <- sapply(data2$Visibility.mi., fun1)
##使用0填补降水量的缺失值
data2$Precipitation.in.[data1$Precipitation.in. %>% is.na()] <- 0
##测试各个变量之间有无显著线性关系
symnum(cor(data1 %>% select(Severity,Start_Lat,Start_Lng,Distance.mi.,Temperature.F.,Humidity...,Pressure.in.,
                            Pressure.in.,Visibility.mi.,Wind_Speed.mph.,Precipitation.in.), use="complete.obs"))
##对风速使用前值插补法
data2$Wind_Speed.mph.[1:5] <- zoo::na.locf(data1$Wind_Speed.mph.[1:5],fromLast = T)
data2$Wind_Speed.mph. <- zoo::na.locf(data1$Wind_Speed.mph.)
head(data2)
#table(is.na(data2$Precipitation.in.))

对27个变量的解释如下：

“Severity” 显示事故的严重程度1-4 ；
“Start_Time” 在本地时区事故的开始时间；
“Street” 街道名称；
“Side” 事故发生在哪一侧（L/R）；
“City” 城市名；
“County” 乡镇名；
“State” 州名；
“Country” 国家US ；
“Temperature.F.” 温度；
“Humidity…” 湿度；
“Pressure.in.” 气压；
“Visibility.mi.” 能见度；
“Wind_Direction” 风向；
“Weather_Condition” 天气状况（雨、雪等）；
“Amenity” 附近有无便利设施；
“Bump” 附近有无减速带；
“Crossing” 附近有无交叉路口；
“Give_Way” 附近有无该标志；
“Junction” 附近是否是交界处；
“No_Exit” 附近有无该标志；
“Railway” 附近有无铁路；
“Roundabout” 附近有无回旋处；
“Station” 附近有无车站；
“Stop” 附近有无停车标志；
Traffic_Calming" 附近有无该标志；
“Traffic_Signal” 附近有无该标志；
“Turning_Loop” 附近有无转弯提示；
"Sunrise_Sunset " 白天或晚上

2.2 各州事故总数

各州在2016-2020年间事故发生总数如下：

#----------------分析各个州之间的数据----------
data3 <-
  data2 %>%
  group_by(State) %>%
  count %>%
  ungroup
data3 %>% nrow
data3

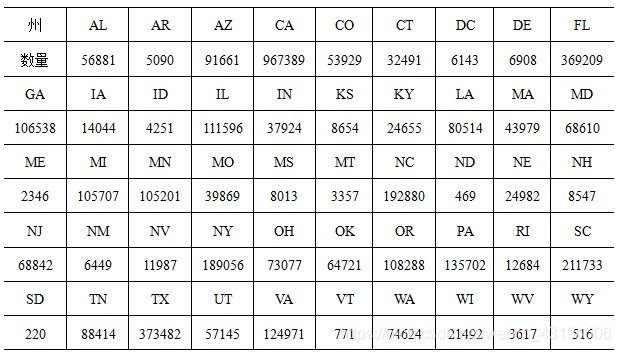
在表中可以看到，事故发生量最多的州为CA（California），CA为美国第一大州，其经济总量在2019年约等于世界第五大经济体。经济繁荣必然伴随着交通的发达，同时交通事故发生的数量也会增大。

##--------------------事故发生地图---------------
install.packages('maps')
install.packages('ggmap')
library(maps)
library(ggmap)
m <- borders("state",colour = "gray50",fill="white")
df2 <- data2 %>% select(Start_Lat,Start_Lng)  
point <- df2[sample(nrow(df2),3000),]
p1 <- ggplot(point,aes(x=Start_Lng,y=Start_Lat)) + m 
p1 + geom_point(color='steelblue',alpha=.6) + 
  labs(title='美国交通事故地图')+ 
  theme(plot.title = element_text(hjust = 0.5))

2.3时间处理

原始数据包含了2016-2020年五年间的数据，五年事故总数如下表所示：
2016-2020事故总数

年份	2016	2017	2018	2019	2020
数量	408868	712186	885327	949400	1253847

由于事故数量庞大，本文提取出2020年的数据进行统计分析。

3影响因素

3.1天气状况

本文将数据中Weather_Condition变量提出进行分析，看到该变量有85个不同的值，于是本文选取总数大于5000 的11个值，对这11个天气状况与事故出现的严重程度的关系进行交叉分析如下图所示。

#---------------提取某一年的数据进行分析-------
data2$year <- year(data2$Start_Time)
summary(data2$year)
#选择2020年的数据
data4 <- data2[data2$year == 2020,]
head(data4)
colnames(data4)
#--------------探究影响车祸程度的因子--------
data4$Severity <- as.factor(data4$Severity)
data4$Wind_Direction <- as.factor(data4$Wind_Direction)
data4$Weather_Condition <- as.factor(data4$Weather_Condition)#设为因子
str(data4)   #查看数据类型
#封装绘图函数
# data：数据源，xlab：x轴数据，fillc：填充颜色，
#pos：调整位置，xname：x轴标签文本，yname：y轴标签文本
fun_bar <- function(data, xlab, fillc, pos, xname, yname) {
  ggplot(data, aes(xlab, fill = fillc)) + 
    geom_bar(position = pos) + 
    labs(x = xname, y = yname) + 
    coord_flip() +
    theme_minimal()
}
#-----------探索不同天气状况的时候对事故程度的影响-------------
#天气状况很多，只画出一部分
rm(x1,x2,x3,x4)
x1 <-
  data4 %>%
  group_by(Weather_Condition) %>%
  count %>%
  ungroup
table(x1)
#选取weather出现的数量大于5000的
#data_wea <- subset(data4, select = c(Weather_Condition,Severity))
#data_wea <- data_wea[data_wea$Weather_Condition != "",]
table(data4$Weather_Condition)   #有空值
data5 <- data4[data4$Weather_Condition != "",]
df3 <- data5 %>% group_by(Weather_Condition) %>% dplyr::summarize(count=n())
#按照天气状况分类统计个数，挑选出个数大于5000的情况
df4 = df3[df3$count > 5000,]   #选出11个
a <- df4$Weather_Condition #selected weathers
data6 <- data5[which(data5$Weather_Condition %in% a),]
data7 <- subset(data6, select = c(Weather_Condition, Severity))
df5 <-
  data7 %>%
  group_by(Weather_Condition,Severity) %>%
  count 
df5   #交叉分析统计出11个最常出现的天气下对应程度1-4的个数
write.csv(df5,"D:/R数据/US_Accidents_2020_weather.csv", row.names=F)
#ggplot(data7,aes(x=Weather_Condition,fill=Severity))+geom_bar(position="dodge")
p3 <- fun_bar(data = data7, xlab = data7$Weather_Condition,
              fillc = data7$Severity,  #堆积条形图
              pos = 'fill', xname = 'weather', yname = 'severity')
p3
#rm(data7)

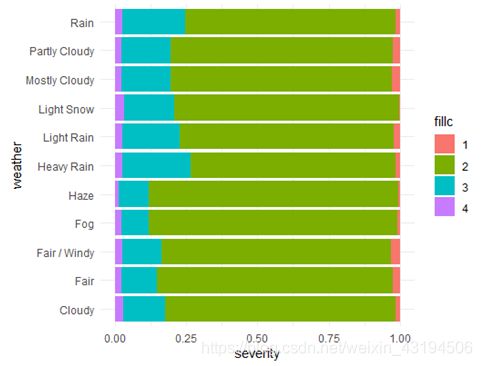
从上图可以看出发生事故最多的11个天气状况都为云雾或雨天，其中暴雨（Heavy Rain）对事故的影响相对较大，更容易照成严重的交通事故。
随后，本文选择Temperature.F.变量进行分析，画出事故数量与温度变化的直方图：

#-----------探索不同温度的时候对事故发生的影响-------------
data8 <- subset(data4, select = c(Temperature.F.))
table(is.na(data8$Temperature.F.))   #有29615个缺失值
data8 <- na.omit(data8)   #删除缺失值
binsize <- diff(range(data8$Temperature.F.))/80
ggplot(data8, aes(x = Temperature.F.)) + geom_histogram(aes(y = ..density..), binwidth = binsize,
                                                        fill = "pink", colour = "blue")+
  stat_function(fun = dnorm, args = list(mean(data8$Temperature.F.), sd(data8$Temperature.F.)), 
                size = 1) + geom_density(colour = "blue", size = 1)
rm(data8)

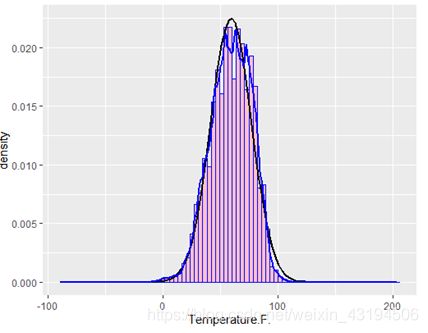
事故发生时的温度主要集中在50-70F左右，此温度接近人体最适宜温度，会有更多人的出门，增大事故发生的机率。
随后选择Humidity…、Pressure.in.、Visibility.mi.三个变量进行分析，画出三者分别对事故发生数量的影响如下：

#-----------探索不同湿度的时候对事故发生的影响-------------
data8 <- subset(data4, select = c(Humidity...))
table(is.na(data8$Humidity...))   #有32072个缺失值
data8 <- na.omit(data8)   #删除缺失值
binsize <- diff(range(data8$Humidity...))/40
ggplot(data8, aes(x = Humidity...)) + geom_histogram(aes(y = ..density..), binwidth = binsize,
                                                        fill = "pink", colour = "blue")+
  stat_function(fun = dnorm, args = list(mean(data8$Humidity...), sd(data8$Humidity...)), 
                size = 1) + geom_density(colour = "blue", size = 1)
rm(data8)

#-----------探索不同气压的时候对事故发生的影响-------------
data8 <- subset(data4, select = c(Pressure.in.))
table(is.na(data8$Pressure.in.))   #有32072个缺失值
data8 <- na.omit(data8)   #删除缺失值
binsize <- diff(range(data8$Pressure.in.))/40
ggplot(data8, aes(x = Pressure.in.)) + geom_histogram(aes(y = ..density..), binwidth = binsize,
                                                     fill = "pink", colour = "blue")+
  stat_function(fun = dnorm, args = list(mean(data8$Pressure.in.), sd(data8$Pressure.in.)), 
                size = 1) + geom_density(colour = "blue", size = 1)
rm(data8)

#-----------探索不同能见度的时候对事故发生的影响-------------
data8 <- subset(data4, select = c(Visibility.mi.))
table(is.na(data8$Visibility.mi.))   #有32072个缺失值
data8 <- na.omit(data8)   #删除缺失值
binsize <- diff(range(data8$Visibility.mi.))/40
ggplot(data8, aes(x = Visibility.mi.)) + geom_histogram(aes(y = ..density..), binwidth = binsize,
                                                      fill = "pink", colour = "blue")+
  stat_function(fun = dnorm, args = list(mean(data8$Visibility.mi.), sd(data8$Visibility.mi.)), 
                size = 1) + geom_density(colour = "blue", size = 1)
rm(data8)

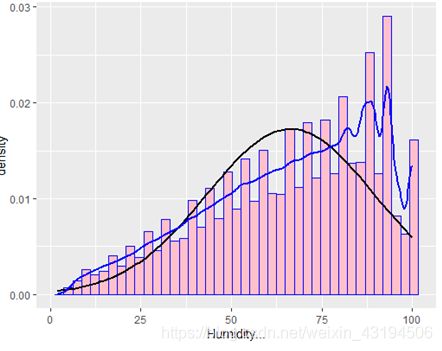
在上图中可明显得看出，能见度低的时候正是事故的高发时期，能见度低会导致车辆和行人视野受限，没有足够的时间应对紧急情况，从而导致事故的发生。
美国大部分地区气候为地中海气候，全年温暖少雨，一年四季阳光充足，十分宜居。从上图也能看出，在天气状况较好时事故发生次数最多。很大原因是天气晴朗时，会有更多人走出家门游玩，人流量和车流量都会相应增大，发生交通事故的可能性也会上升。相比之下，天气状况不好时事故发生数量反而降低，这种天气下，人们会减少出行次数。

3.2时间因素

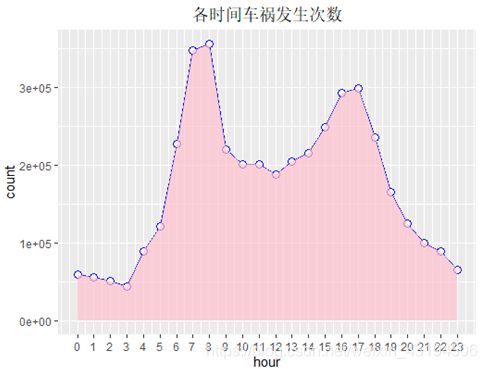
首先，对每天中交通事故发生时间进行分析，作出折线图：

#---------------分析各个时间段发生事故的数据----------
head(data2)
data2$Start_Time <- as.POSIXct(data2$Start_Time)#设置时间格式
data2$St_hour <- hour(data2$Start_Time)
df1 <- data2 %>% group_by(St_hour) %>% dplyr::summarize(count=n())
p2 <- ggplot(df1,aes(x=St_hour,y=count,fill='pink'))
p2 + geom_line(linetype=1,color='blue')+
  geom_point(size = 3, shape = 21, colour = "blue",fill='white')+
  geom_area(fill = 'pink',alpha=.7)+
  scale_x_continuous(breaks = c(0:23),name='hour')+
  labs(title='各时间车祸发生次数')+ 
  theme(plot.title = element_text(hjust = 0.5))
#rm(df1)
data2$mon <- month(data2$Start_Time)
df1 <- data2 %>% group_by(mon) %>% dplyr::summarize(count=n())
p2 <- ggplot(df1,aes(x=mon,y=count,fill='pink'))
p2 + geom_line(linetype=1,color='blue')+
  geom_point(size = 3, shape = 21, colour = "blue",fill='white')+
  geom_area(fill = 'pink',alpha=.7)+
  scale_x_continuous(breaks = c(0:23),name='month')+
  labs(title='各月车祸发生次数')+ 
  theme(plot.title = element_text(hjust = 0.5))
write.csv(data2,"D:/R数据/data2.csv", row.names=F)

从上图可知，一天之中两个事故发生高峰期位于早上6-9点与下午4-6点之间，这与人们的生活作息相关，如这两段时间内人们会集中上下班和上学放学。
对于每年中交通事故在各月中出现的次数进行分析，探查其季节规律，绘出折线图如下：

由上图可知，2016-2020年间美国在上半年的事故数明显少于后半年的事故数。

3.3路况因素

对于路况、白天黑夜这样的环境因素对于事故发生的影响，我们选取多个逻辑变量进行探寻，绘制出环境因素的堆积条形图如下：

#------------探索定性变量对事故的影响--------------
library(plyr)
library(magrittr)
data9 <- subset(data4, select = c(Crossing, Sunrise_Sunset, Precipitation.in., Traffic_Signal,
                                  Give_Way, Junction, Bump, Station, Railway, Traffic_Calming,
                                  Turning_Loop))
#Traffic_condition <- data1 %>% select(Crossing,Sunrise_Sunset,Precipitation.in.,Traffic_Signal,Give_Way,Bump)
#将降雨量转化为逻辑变量
data9$Precipitation.in.[data9$Precipitation.in. > 0] <- 'True'
data9$Precipitation.in.[data9$Precipitation.in. == 0] <- 'False'
head(data9)
#查看各个变量的结构
table(data9$Sunrise_Sunset) #Sunrise_Sunset中有空值，删去
data9 <- data9[data9$Sunrise_Sunset != "",]
data9$Sunrise_Sunset[data9$Sunrise_Sunset == 'Day'] <- 'True'
data9$Sunrise_Sunset[data9$Sunrise_Sunset == 'Night'] <- 'False'
df6 <- rbind(colSums(data9=='True'),colSums(data9=='False')) %>%cbind(Boolean=c('True','False')) %>% data.frame()
data_env <- melt(df6,
                id.vars = 'Boolean',
                variable.name = 'Environ',
                value.name = 'Accidents'
)
str(data_env)   #Accidents为字符型数据，转换为数值型
data_env$Accidents <- as.numeric(data_env$Accidents)
x1 <- ddply(data_env,'Environ',transform,
            percent_num = Accidents/sum(Accidents)*100)
p4 <- ggplot(x1,aes(x=Environ,y=percent_num,fill=Boolean))
p4 + geom_bar(stat = 'identity',color='blue')+ 
  scale_fill_brewer(palette = 11)+
  geom_text(aes(label=paste(round(percent_num),"%"),vjust=-0.3))+
  labs(title='环境因素堆积条形图')+ 
  theme(plot.title = element_text(hjust = 0.5))

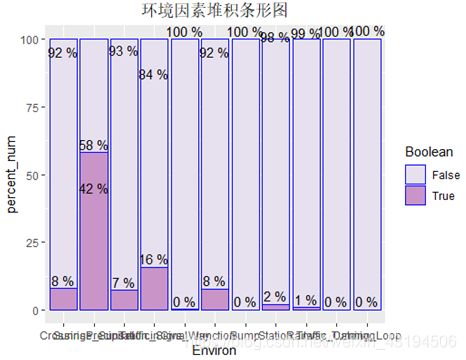
从上图可知，交通事故主要发生道路交界处、交通信号灯、车站等地方。这些地方往往路况比较复杂，车流量和人流量都比较大，容易发生交通事故。尤其是十字交叉路口，四个方向的车汇集此处，相比普通路段，碰撞的概率大大增加。

4 预测分析

本文选取Crossing、Sunrise_Sunset、Precipitation.in.、Traffic_Signal、Junction、Station、Railway、Temperature.F.、Humidity…、Pressure.in.、Visibility.mi.、St_hour、mon这13个因子对事故的严重程度建立模型进行预测。其中，将逻辑变量转化为数值型的0、1，将所有因子转化为数值型变量进行xgboost模型的建立。

#--------------------预测--------------------
install.packages('xgboost')
library(xgboost)
#由上述分析中，将有用指标提取出来
data4$mon <- month(data4$Start_Time)
data0 <- subset(data4, select = c(Crossing, Sunrise_Sunset, Precipitation.in., Traffic_Signal, Junction,
                                  Station, Railway, Temperature.F., Humidity..., Pressure.in., Visibility.mi.,
                                  St_hour, mon, Severity))
table(data0$Sunrise_Sunset)
data0 <- data0[which(data0$Sunrise_Sunset!=''),]
data0$Sunrise_Sunset[data0$Sunrise_Sunset=='Night'] <- 'False'
data0$Sunrise_Sunset[data0$Sunrise_Sunset=='Day'] <- 'True'
data0[data0=='False'] <- 0
data0[data0=='True'] <- 1
str(data0)
colnames(data0)
#将变量值转化为数值型
data0[,1:13] <- data0[,1:13] %>% apply(2,as.numeric) %>% data.frame()
y <- data0$Severity
X <- scale(data0[,-14],scale = T) %>% data.matrix()
bst <- xgb.cv(data = X,label = y,max.depth=12,eta=0.007,nrounds = 10,
              objective = "multi:softmax",num_class=5,nfold = 5,booster='gbtree')

xgmodel <- xgboost(data = X,label = y,max.depth=12,eta=0.007,nrounds = 10,
                   objective = "multi:softmax",num_class=5,booster='gbtree')
pre_y <- predict(xgmodel,X)#预测值
accuracy <- sum(pre_y==y)/length(y)#计算准确率
accuracy

最后计算出模型的准确率为0.816472，模型比较合适。

5 总结

1. 美国交通事故发生最多的州是加利福尼亚州，并且交通事故数量逐年上升。
2. 影响交通事故的主要因素有天气、路况、出行时间等。天气越好，路况越差，事故发生越频繁；
3. 出行时间则与人们的生活作息有关。各城市经济越发达，事故发生次数也越多。
4. 我们在外出之时，需要注意路况，在交叉路口、转弯标识等处注意车辆和行人。