LIQING LIN

ts7_Missing_imputation_interpolation_MICE_NaN NaT fillNA_IterativeImputer_FeatureUnion_iloc_识别列表连续组

As a data scientist, data analyst, or business analyst, you have probably discovered that obtaining a perfect clean dataset is too optimistic. What is more common, though, is that the data you are working with suffers from faws such as missing values, erroneous/ɪˈroʊniəs/ data, duplicate records, insuffcient data, or the presence of outliers in the data.

Time series data is no different, and before plugging the data into any analysis or modeling workflow, you must investigate the data first. It is vital to understand the business context around the time series data to detect and identify these problems successfully. For example, if you work with stock data, the context is very different from COVID data or sensor data.

Having that intuition or domain knowledge will allow you to anticipate what to expect and what is considered acceptable when analyzing the data. Always try to understand the business context around the data. For example, why is the data collected in the first place? How was the data collected? What business rules, logic, or transformations have been applied to the data? Were these modifications applied during the data acquisition/ˌækwɪˈzɪʃ(ə)n/(金钱、财物等的)获取 process or built into the systems that generate the data?

During the discovery phase, such prior knowledge will help you determine the best approach to clean and prepare your dataset for analysis or modeling. Missing data and outliers are two common problems that need to be dealt with during data cleaning and preparation. You will dive into outlier detection in ts8_Outlier Detection_plotly_sns_text annot_modified z-score_hist_Tukey box_cdf_resample freq_Quanti_LIQING LIN的博客-CSDN博客, Outlier Detection Using Statistical Methods, and Chapter 14, Outlier Detection Using Unsupervised Machine Learning. In this chapter, you will explore techniques to handle missing data through imputation插补 and interpolation插值.

Here is the list of recipes that we will cover in this chapter:

Performing data quality checks
Handling missing data with univariate imputation using pandas
Handling missing data with univariate imputation using scikit-learn
Handling missing data with multivariate imputation
Handling missing data with interpolation

In this chapter, two datasets will be used extensively for the imputation and interpolation recipes: the CO2 Emissions/ɪˈmɪʃ(ə)n/(尤指光/热/气等的)散发,排放 dataset, and the e-Shop Clickstream dataset. The source for the Clickstream dataset comes from clickstream data for online shopping from the UCI machine learning repository, which you can find here: https://archive.ics.uci.edu/ml/datasets/clickstream+data+for+online+shopping

The source for the CO2 emissions dataset comes from the Annual CO2 emissions report from Our World in Data, which you can find here: https://ourworldindata.org/co2-emissions.

For demonstration purposes, the two datasets have been modified by removing observations (missing data). The original versions are provided, in addition to the modified versions, to be used for evaluating the different techniques discussed in this chapter.

Throughout this chapter, you will follow similar steps for handling missing data: ingest/ɪnˈdʒest/摄取 the data into a DataFrame, identify missing data, impute missing data, evaluate it against the original data, and finally, visualize and compare the different imputation techniques.

These steps can be translated into functions for reusability. You can create functions for these steps in the process: a function to read the data into a DataFrame, a function to evaluate using the RMSE score, and a function to plot the results.

Understanding missing data

Data can be missing for a variety of reasons, such as unexpected power outages, a device that got accidentally unplugged, a sensor that just became defective/dɪˈfektɪv/有问题的,有缺陷的, a survey respondent declined to answer a question, or the data was intentionally removed for privacy and compliance/kəmˈplaɪəns/合规 reasons. In other words, missing data is inevitable.

Generally, missing data is very common, yet sometimes it is not given the proper level of attention in terms of formulating a strategy on how to handle the situation.

One approach for handling rows with missing data is to drop those observations (delete the rows). However, this may not be a good strategy if you have limited data in the first place, for example, if collecting the data is a complex and expensive process. Additionally, the drawback of deleting records, if done prematurely/ˌpreməˈtʃʊəli/过早地, is that you will not know if the missing data was due to censoring/ˈsensərɪŋ/审查 (an observation is only partially collected) or due to bias (for example, high-income participants declining to share their total household income in a survey).

A second approach may involve tagging the rows with missing data by adding a column describing or labeling the missing data. For example, suppose you know that there was a power outage on a particular day. In that case, you can add Power Outage to label the missing data and differentiate it from other missing data labeled with Missing Data if the cause is unknown.

A third approach, which this chapter is about, is estimating the missing data values. The methods can range from simple and naive to more complex techniques leveraging machine learning and complex statistical models. But how can you measure the accuracy of the estimated values for data missing in the first place?

There are different options and measures to consider, and the answer is not as simple. Therefore, you should explore different approaches, emphasizing a thorough evaluation and validation process to ensure the selected method is ideal for your situation. In this chapter, you will use Root Mean Squared Error (RMSE) to evaluate the different imputation techniques.

The process to calculate the RMSE can be broken down into a few simple steps: first, computing the error, which is the difference between the actual values and the predicted or estimated values. This is done for each observation. Since the errors may be either negative or positive, and to avoid having a zero summation, the errors (differences) are squared. Finally, all the errors are summed and divided by the total number of observations to compute the mean. This gives you the Mean Squared Error (MSE). RMSE is just the square root of the MSE.

The RMSE equation can be written as: $\large RMSE = \sqrt{\frac{\sum_{i=1}^{N}(x_i - \hat{x}_i)}{N}}$

In our estimate of the missing observations, $\large \hat{x}_i$ is the imputed value估算值, $\large x_i$ is the actual (original) value, and N is the number of observations.

RMSE for Evaluating Multiple Imputation Methods

I want to point out that RMSE is commonly used to measure the performance of predictive models (for example, comparing regression models). Generally, a lower RMSE is desirable; it tells us that the model can fit the dataset. Simply stated, it tells us the average distance (error) between the predicted value and the actual value. You want this distance minimized.

When comparing different imputation methods, we want our imputed values to resemble (as close as possible) the actual data, which contains random effects (uncertainty). This means we are not seeking a perfect prediction, and thus a lower RMSE score does not necessarily indicate a better imputation method. Ideally, you would want to find a balance, hence, in this chapter, the use of RMSE is combined with visualization to help illustrate how the different techniques compare and work.

As a reminder, we have intentionally removed some values (synthetically causing missing data) but retained the original data to compare against for when using RMSE.

Performing data quality checks

Missing data are values not captured or observed in the dataset. Values can be missing for a particular feature (column), or an entire observation (row). When ingesting the data using pandas, missing values will show up as either NaN, NaT, or NA.

Sometimes, missing observations are replaced with other values in the source system; for example, this can be a numeric filler such as 99999 or 0, or a string such as missing or N/A . When missing values are represented by 0, you need to be cautious and investigate further to determine whether those zero values are legitimate or they are indicative of missing data.

The pandas library provides convenient methods for discovering missing data and for summarizing data in a DataFrame:

pandas.read_csv — pandas 1.5.2 documentation

When reading the CSV files using pandas.read_csv() , the default behavior is to recognize and parse certain string values, such as NA , N/A , and null, to the NaN type (missing). Thus, once these values became NaN , the CSV reader could parse the co2 column as float64 (numeric) based on the remaining non-null values.

This is possible due to two parameters: na_values and keep_default_na . The na_values parameter, by default, contains a list of strings that are interpreted as NaN .
The list includes ‘#N/A’, ‘#N/A N/A’, ‘#NA’, ‘-1.#IND’, ‘-1.#QNAN’, ‘-NaN’, ‘-nan’, ‘1.#IND’, ‘1.#QNAN’, ‘’, ‘N/A’, ‘NA’, ‘NULL’, ‘NaN’, ‘n/a’, ‘nan’, ‘null’.

You can append to this list by providing additional values to the na_values parameter. Additionally, keep_default_na is set to True by default, thus using na_values with the default list for parsing.

keep_default_na bool, default True

Whether or not to include the default NaN values when parsing the data. Depending on whether na_values is passed in, the behavior is as follows:

If keep_default_na is True, and na_values are specified, na_values is appended to the default NaN values used for parsing.
If keep_default_na is True, and na_values are not specified, only the default NaN values are used for parsing.
If keep_default_na is False, and na_values are specified, only the NaN values specified na_values are used for parsing.
If keep_default_na is False, and na_values are not specified, no strings will be parsed as NaN.

Note that if na_filter is passed in as False, the keep_default_na and na_values parameters will be ignored.

1. Start by reading the two CSV fles, co2_missing.csv and clicks_missing_multiple.csv
......

import pandas as pd

ecom = 'https://raw.githubusercontent.com/PacktPublishing/Time-Series-Analysis-with-Python-Cookbook/main/datasets/Ch7/clicks_missing_multiple.csv'

ecom_df = pd.read_csv( ecom,
                       index_col='date', #####
                       parse_dates=True
                     )
ecom_df

Figure 7.1 – First five rows from the ecom_df DataFrame showing NaN and NaT

The output from the preceding code shows that there are five missing values from the source dataset.

NaN is how pandas represents empty numeric values (NaN is short for Not a Number).
NaT is how pandas represents missing Datetime values (NaT is short for Not a Time).

2. To count the number of missing values in both DataFrames, you can use the DataFrame.isnull() method. This will return True (if missing) or False (if not missing) for each value. For example, to get the total count of missing values for each column, you can use DataFrame.isnull().sum() .

m05_Extract Feature_Transformers(慎variances_)_download Adult互联网ads数据集_null value(?_csv_SVD_PCA_eigen_LIQING LIN的博客-CSDN博客

In Python, Booleans ( True or False ) are a subtype of integers. True is equivalent to 1 , and False is equivalent to 0. To validate this concept, try the following:

isinstance(True, int)

int(True)

Now, let's get the total number of missing values for each DataFrame:

ecom_df.isna().sum()

pandas.DataFrame.isna — pandas 1.5.2 documentation

ecom_df.isnull().sum()

(NaT is short for Not a Time)

ecom_df.index

ecom_df.reset_index().isna().sum()

ecom_df.reset_index().isnull().sum()

ecom_df.reset_index()

pandas automatically convert the empty values to np.NaN (missing)

import pandas as pd

ecom = 'https://raw.githubusercontent.com/PacktPublishing/Time-Series-Analysis-with-Python-Cookbook/main/datasets/Ch7/clicks_missing_multiple.csv'

ecom_df = pd.read_csv( ecom,
                       #index_col='date',
                       parse_dates=True
                     )
ecom_df[43:61]

<==
co2_missing.csv

.........

...

...

co2='https://raw.githubusercontent.com/PacktPublishing/Time-Series-Analysis-with-Python-Cookbook/main/datasets/Ch7/co2_missing.csv'

co2_df = pd.read_csv( co2,
                      #index_col='date',
                      parse_dates=True
                    )
co2_df.iloc[50:64]

<==

auto convert the string placeholder(NaN, NaT, NA) values to np.NaN (missing)

co2_df[178:195]

<==

co2_df.isnull().sum()

co2_df.isna().sum()

Notice in the preceding code that both .isnull() and .isna() were used. They both can be used interchangeably since .isnull() is an alias of .isna() .

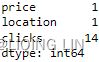
From the results, co2_df has 25 missing values from the co2 column, while ecom_df has 20 missing values in total ( 4 from the date column, 1 from the price column, 1 from the location column, and 14 from the clicks column).

3. To get the grand total for the entire ecom_df DataFrame, just chain another .sum() function to the end of the statement:

ecom_df.isnull().sum().sum()

co2_df.isna().sum().sum()

4. If you inspect the co2_missing.csv file using a text/code editor, Excel, or Jupyter (Notebook or Lab) and scroll down to rows 192-194, you will notice that there are string placeholder values in there: NA , N/A , and null.
Figure 7.2 – co2_missing.csv shows string placeholder values that were converted to NaN (missing) by pandas

5. If all you need is to check whether the DataFrame contains any missing values, use isnull().values.any() . This will output True if there are any missing values in the DataFrame:

ecom_df.isnull().values.any()

co2_df.isnull().values.any()

6. So far, .isnull() helped identify all the missing values in the DataFrames.

co2_df.isnull()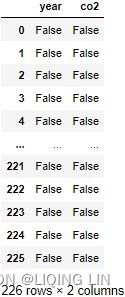

But what if the missing values were masked or replaced by other placeholder values such as ? or 99999. The presence of these values will be skipped and considered missing (NaN) in pandas( ?:m05_Extract Feature_Transformers(慎variances_)_download Adult互联网ads数据集_null value(?_csv_SVD_PCA_eigen_LIQING LIN的博客-CSDN博客

solutions:

import numpy as np
adult = adult.replace( to_replace=r'\?', value=np.nan, regex=True)
adult.iloc[10:16]

). Technically, they are not empty cells (missing) and hold values. On the other hand, domain or prior knowledge will tell us that the CO2 emission dataset is measured annually and should have values greater than 0.

Similarly, we expect the number of clicks to be numeric for the Clickstream data. If the column is not numeric, it should trigger an investigation as to why pandas could not parse the column as numeric. For example, this could be due to the presence of string values.

To gain a better insight into the DataFrame schema and data types, you can use DataFrame.info() to display the schema, total records, column names, column dtypes, count of non-missing values per column, index dtype, and the DataFrame's total memory usage:

co2_df.info()

The co2_df summary output looks reasonable, confirming that we have 25 (226-221=25) missing values in the co2 column.

ecom_df.info()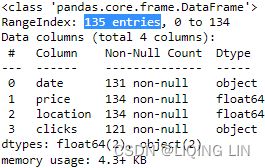

On the other hand, the summary for ecom_df indicates that the clicks column is of the object dtype, and not the expected float64(we expect the number of clicks to be numeric for the Clickstream data). Let's investigate further using basic summary statistics.

7. To get the summary statistics for a DataFrame, use the DataFrame.describe() method:

include ‘all’, list-like of dtypes or None (default), optional
A white list of data types to include in the result. Ignored for Series. Here are the options:

‘all’ : All columns of the input will be included in the output.

A list-like of dtypes : Limits the results to the provided data types.

To limit the result to numeric types submit numpy.number.
```
include=[np.number]
```
To limit it instead to object columns submit the numpy.object data type.
```
include=[object]
```
Strings can also be used in the style of select_dtypes (e.g. df.describe(include=['O'])).
To select pandas categorical columns, use 'category'
```
include=['category']
```

None (default) : The result will include all numeric columns.

exclude list-like of dtypes or None (default), optional,
A black list of data types to omit from the result. Ignored for Series. Here are the options:

A list-like of dtypes : Excludes the provided data types from the result.

To exclude numeric types submit numpy.number.
```
exclude=[np.number]
```
To exclude object columns submit the data type numpy.object.
```
exclude=[object]
```
Strings can also be used in the style of select_dtypes (e.g. df.describe(exclude=['O'])).
To exclude pandas categorical columns, use 'category'

None (default) : The result will exclude nothing.

datetime_is_numeric bool, default False
Whether to treat datetime dtypes as numeric. This affects statistics calculated for the column. For DataFrame input, this also controls whether datetime columns are included by default.

co2_df.describe( include='all',
                 datetime_is_numeric=True
               )

Figure 7.4 – co2_df summary statistics indicating zero values present in the data

Note the use of include=' all' to replace the default value None . The default behavior is to show summary statistics for only numeric columns. By changing the value to 'all' , the results will include all column types.

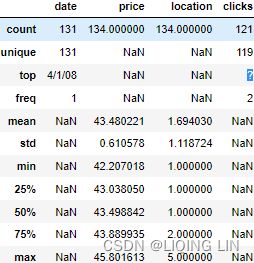
The summary statistics for the co2_df DataFrame confirms that we have zero values under the missing column (min = 0.00). As pointed out earlier, prior knowledge tells us that 0 represents a null (or missing) value. Therefore, the zeros will need to be replaced with NaN to include such values in the imputation process. Now, review the summary statistics for ecom_df .

ecom_df.describe( include=None,
                  datetime_is_numeric=True
                )

the default behavior is to show summary statistics for only numeric columns.

ecom_df.describe( include='all',
                  datetime_is_numeric=True
                )

OR include=[np.number]

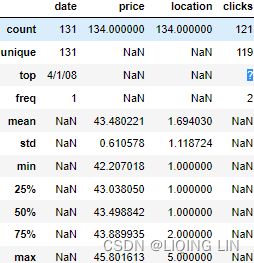Figure 7.5 – ecom_df summary statistics indicating the ? value in the clicks column

As you can see, the summary statistics for the ecom_df DataFrame indicate that we have a ? value under the clicks column. This explains why pandas did not parse the column as numeric (due to mixed types). Similarly, the ? values will need to be replaced with NaN to be treated as missing values for imputation.

Convert the 0 and ? values to NaN types

8. Convert the 0 and ? values to NaN types. This can be accomplished using the DataFrame.replace() method:

import numpy as np

co2_df.replace( to_replace=0, value=np.NaN, 
                inplace=True
              )
co2_df.isnull().sum()

<==

co2_df.describe( include='all',
                 datetime_is_numeric=True
               )

<==

ecom_df.replace( to_replace='?', value=np.NaN,
                 inplace=True
               )
ecom_df.isnull().sum()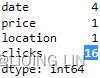

<==
sometimes, we need to call .replace( to_replace=r'\?', value=np.nan, regex=True)

ecom_df.describe( include='all',
                  datetime_is_numeric=True
                )

<==

ecom_df[43:61]

<==

Covert the dtype(such as object) to the expected dtype(such as object)

we expect the number of clicks to be numeric for the Clickstream data

ecom_df['clicks'] = ecom_df['clicks'].astype('float')
ecom_df.info()

<==

ecom_df.isnull().sum()

The new numbers do a better job of reflecting the number of actual missing values in both DataFrames.

If you change keep_default_na to False without providing new values to na_values , then none of the strings ( NA , N/A , and null ) would be parsed to NaN unless you provide a custom list. For example, if keep_default_na was set to False and no values provided to na_values , then the entire co2 column would be parsed as a string (object), and any missing values will show up as strings; in other words, they will be coming in as ' ' , which is an empty string.

keep_default_na bool, default True

Whether or not to include the default NaN values when parsing the data. Depending on whether na_values is passed in, the behavior is as follows:

If keep_default_na is True, and na_values are specified, na_values is appended to the default NaN values used for parsing.
If keep_default_na is True, and na_values are not specified, only the default NaN values are used for parsing.
If keep_default_na is False, and na_values are specified, only the NaN values specified na_values are used for parsing.
If keep_default_na is False, and na_values are not specified, no strings will be parsed as NaN.

co2='https://raw.githubusercontent.com/PacktPublishing/Time-Series-Analysis-with-Python-Cookbook/main/datasets/Ch7/co2_missing.csv'

co2_df2 = pd.read_csv( co2,
                      #index_col='date',
                      parse_dates=True,
                      keep_default_na=False, # na_values are not specified,
                    )                        # no strings will be parsed as NaN
co2_df2[178:195]

<== vs keep_default_na=True==>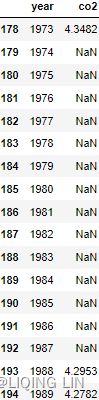
Figure 7.6 – Output from the co2_df DataFrame without NaN parsing

You will notice serveral rows have blank values (empty string).

co2_df2.isna().sum()

vs keep_default_na=True ==>

co2_df2.info()

Notice the change in dtype for the co2 columns.

vs keep_default_na=True==>

In this recipe you explored the .isna() method. Once the data is read into a DataFrame or series, you get access to the .isna() and .isnull() methods, which return True if data is missing and False otherwise. To get the counts for each column, we just chain a .sum() function, and to get the grand total, we chain another .sum() function following that:

co2_df2.isnull().sum().sum()

If you know that the data will always contain ? , which should be converted to NaN (or any other value), then you can utilize the pd.read_csv() function and update the na_values parameter. This will reduce the number of steps needed to clean the data after creating the DataFrame:

pd.read_csv( ecom,
             #index_col='date',
             parse_dates=['date'],
             na_values={'?'},
             # keep_default_na = True(default)
           )[43:61] # na_values is appended to the default NaN values

<==

Tis will replace all instances of ? and blank values with NaN

pd.read_csv( ecom,
             #index_col='date',
             parse_dates=['date'],
             na_values={'?'},
             # keep_default_na = True(default) # na_values is appended to the default NaN values
           ).isna().sum()

Handling missing data with univariate imputation插补 using pandas

Generally, there are two approaches to imputing missing data: univariate imputation and multivariate imputation. This recipe will explore univariate imputation techniques available in pandas.

In univariate imputation, you use non-missing values in a single variable (think a column or feature) to impute the missing values for that variable. For example, if you have a sales column in the dataset with some missing values, you can use a univariate imputation method to impute missing sales observations using average sales. Here, a single column (sales) was used to calculate the mean (from non-missing values) for imputation.

Some basic univariate imputation techniques include the following:

• Imputing using the mean.
• Imputing using the last observation forward (forward fill). This can be referred to as Last Observation Carried Forward (LOCF).
• Imputing using the next observation backward (backward fill). This can be referred to as Next Observation Carried Backward (NOCB).

You will use two datasets to impute missing data using different techniques and then compare the results.

You will start by importing the libraries and then read all four CSV files. You will use the original versions of datasets to compare the results of the imputations to gain a better intuition of how they perform. For the comparison measure, you will use RMSE to evaluate each technique and then visualize the outputs to compare the imputation results visually:

1. Use the read_csv() function to read the four datasets:

folder = 'https://raw.githubusercontent.com/PacktPublishing/Time-Series-Analysis-with-Python-Cookbook/main/datasets/Ch7'

co2_original = pd.read_csv( folder + '/co2_original.csv', 
                            #index_col='year',
                            parse_dates=True
                          )
co2_missing = pd.read_csv( folder + '/co2_missing_only.csv',
                           #index_col='year',
                           parse_dates=True
                         )

clicks_original = pd.read_csv( folder + '/clicks_original.csv',
                               #index_col='date',
                               parse_dates=True
                             )
clicks_missing = pd.read_csv( folder + '/clicks_missing.csv',
                              #index_col='date',
                              parse_dates=True
                            )
co2_missing

year_co2=co2_missing[co2_missing[co2_missing.columns[1]].isnull()][[co2_missing.columns[0],
                                                                    co2_missing.columns[1]
                                                                   ]]
year_co2

import numpy as np

def group_consecutive(a):
    # https://numpy.org/doc/stable/reference/generated/numpy.split.html
    return np.split( a, 
                     np.where( np.diff(a) != 1 )[0] + 1
                   )

group_consecutive(year_co2.index.to_list() )

median_x=[]
median_y=[]
for a in group_consecutive( year_co2.index.to_list() ):
    median_idx=( a[0]+a[-1] )/2
    year, last_co2= co2_missing[co2_missing.index==a[0]-1].iloc[:, 0:2].values[0]
    year, next_co2= co2_missing[co2_missing.index==a[-1]+1].iloc[:, 0:2].values[0]
    median_co2 = ( last_co2 + next_co2)/2
    #print(last_co2, next_co2)
    median_x.append(median_idx)
    median_y.append(median_co2)
    
print(median_x)
print(median_y)

import matplotlib.pyplot as plt
import matplotlib.ticker as ticker

def plot_dfs( df1, df2, col, title=None, xlabel=None, ylabel=None, offset=0.5 ):
    '''
    df1: original dataframe without missing data
    df2: dataframe with missing data
    col: column name that contains missing data
    '''
    m='missing'
    df_missing = df2.rename( columns={col: m} )
    
    columns = df_missing.loc[:, 'missing':].columns.tolist()
    # .columns : Index(['missing'], dtype='object')
    subplots_size = len( columns )
    
    # subplots_size = df2.shape[1]
    fig, ax = plt.subplots( subplots_size+1, 1, sharex = True,
                            figsize=(10,10)
                          )
    plt.subplots_adjust( hspace=0.3 )
    fig.suptitle(title, y=0.92)
    
    #print(np.array( df1[df1.columns[0]].values,))# df1['year'].values
#    df1[col].plot( ax=ax[0] )
    ax[0].plot( np.array( df1[df1.columns[0]].values,),
                df1[col].values,
              )
    
    ax[0].set_title( r'$\bf{Original Dataset}$' )
    ax[0].set_ylabel( ylabel )

    #missing
    for i, columnName in enumerate( columns ):
        #df_missing[columnName].plot( ax=ax[i+1] )  # columnName.capitalize()
        ax[i+1].plot( np.array( df_missing[df_missing.columns[0]].values,),
                      df_missing[columnName].values,
                    )
        ax[i+1].set_title( r'$\bf{}$'.format( columnName.upper() ) )

        if columnName == m:
            for j in range( len(median_x) ):
                ax[i+1].annotate('',#str(median_x[j]),
                                 ha='center', va='center',
                                 xy= (df_missing[df_missing.index==int(median_x[j])][df_missing.columns[0]], 
                                      median_y[j],
                                     ),
                                 xytext=(df_missing[df_missing.index==int(median_x[j])][df_missing.columns[0]],
                                         median_y[j]+offset
                                        ),
                                 arrowprops=dict(arrowstyle='->, head_width=0.5, head_length=0.8',
                                                 facecolor='red',ls="-",
                                                 linewidth=3, edgecolor='red',
                                                )
                                )
    ax[-1].set_xlabel( xlabel )
    ax[-1].xaxis.set_major_locator(ticker.MaxNLocator(12)) 
    plt.setp( ax[-1].get_xticklabels(), rotation=45, horizontalalignment='right', fontsize=10 )
    plt.show()

2. Visualize the CO2 DataFrames (original and missing) and specify the column with missing values ( co2 ):

plot_dfs( co2_original, 
          co2_missing, 
          'co2',
          title="Annual CO2 Emission per Capita",
          xlabel="Years",
          ylabel="x100 million tons"
        )

The plot_dfs function will produce two plots: the original CO2 dataset without missing values, and the altered dataset with missing values.

Figure 7.7–CO2 dataset showing a comparison between the missing values and the original

From Figure 7.7, you can see a noticeable upward trend in CO2 levels over time. There is missing data in three different spots.

clicks_missing

date_clicks=clicks_missing[clicks_missing['clicks'].isnull()][[clicks_missing.columns[0],
                                                               'clicks'
                                                              ]]
date_clicks

median_x=[]
median_y=[]
for a in group_consecutive( date_clicks.index.to_list() ):
    median_idx=( a[0]+a[-1] )/2
    #print(clicks_missing[clicks_missing.index==a[0]-1].values[0][[0,3]])
    year,last_co2= clicks_missing[clicks_missing.index==a[0]-1].values[0][[0,3]]
    year,next_co2= clicks_missing[clicks_missing.index==a[-1]+1].values[0][[0,3]]
    median_co2 = ( last_co2 + next_co2)/2
    #print(last_co2, next_co2)
    median_x.append(median_idx)
    median_y.append(median_co2)
    
print(median_x)
print(median_y)

plot_dfs(clicks_original, clicks_missing, 
         'clicks', 
         title="Page Clicks per Day",
         xlabel='date',
         ylabel='# of clicks',
         offset=5000
        )

Figure 7.8–Clickstream dataset showing a comparison between the missing values and the original

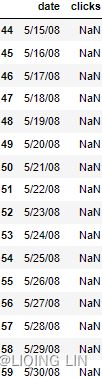
Notice, the output shows missing data from May 15 to May 31. You can confirm this by running the following code:

clicks_missing[ clicks_missing['clicks' ].isna() ]

3. Now you are ready to perform your first imputation. You will use the fillna() method which has a value parameter that takes either a numeric or a string value to substitute for all the NaN instances. Alternatively, instead of using the value parameter, .fillna() has a method parameter that can take specific string values such as ffill for forward fill, or bfill for backward fill.

Using DataFrame.fillna() is the simplest imputation method. The function can be used in two ways depending on which parameter you are using:

The value parameter, where you can pass a scalar value (numeric or string) to use to fill for all missing values
The method parameter, which takes specific string values:
- Backward filling: backfill or bfill , uses the next observation, after the missing spot(s) and flls the gaps backward
- Forward filling: ffill or pad , uses the last value before the missing spot(s) and fills the gaps forward

Let's impute the missing values utilizing the method parameter and append the results as new columns in the DataFrame. Start with the CO2 DataFrame:

co2_missing['ffill'] = co2_missing['co2'].fillna( method='ffill' )
co2_missing['bfill'] = co2_missing['co2'].fillna( method='bfill' )
co2_missing['mean'] = co2_missing['co2'].fillna( co2_missing['co2'].mean() )
co2_missing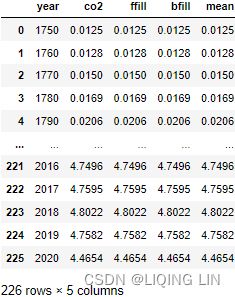

Use the rmse_score function to get the scores:

def rmse_score( df1, df2, col=None ):
    '''
    df1: original dataframe without missing data
    df2: dataframe with missing data
    col: column name that contains missing data
    
    returns: a list of scores
    '''
    df_missing = df2.rename( columns={col: 'missing'} )
    columns = df_missing.loc[:, 'missing':].columns.tolist() # co2, ffill, bfill, mean
    scores = []
    for comp_col in columns[1:]:
        rmse = np.sqrt( np.mean( ( df1[col]-df_missing[comp_col] )**2 ) )
        scores.append( rmse )
        print( f'RMSE for {comp_col}: {rmse}' )
    return scores

_ = rmse_score( co2_original,
                co2_missing,
                'co2'
              )

year_co2=co2_missing[co2_missing[co2_missing.columns[1]].isnull()][[co2_missing.columns[0],
                                                                    co2_missing.columns[1]
                                                                   ]]
median_x=[]
median_y=[]
for a in group_consecutive( year_co2.index.to_list() ):
    median_idx=( a[0]+a[-1] )/2
    year, last_co2= co2_missing[co2_missing.index==a[0]-1].iloc[:, 0:2].values[0]
    year, next_co2= co2_missing[co2_missing.index==a[-1]+1].iloc[:, 0:2].values[0]
    median_co2 = ( last_co2 + next_co2)/2
    #print(last_co2, next_co2)
    median_x.append(median_idx)
    median_y.append(median_co2)
    
print(median_x)
print(median_y)

Now, visualize the results using the plot_dfs function:

plot_dfs( co2_original,
          co2_missing,
          'co2'
        )

The preceding code produces the results as follows:

Figure 7.9 – Comparison between the three imputation methods for the CO2 DataFrame

Compare the results in Figure 7.9 with the original data in Figure 7.7. Notice that both ffill and bfill produce better results than when using the mean. Both techniques have favorable RMSE scores and visual representation.

4. Now, perform the same imputation methods on the Clickstream DataFrame:

clicks_missing['ffill'] = clicks_missing['clicks'].fillna( method='ffill' )
clicks_missing['bfill'] = clicks_missing['clicks'].fillna( method='bfill' )
clicks_missing['mean'] = clicks_missing['clicks'].fillna( clicks_missing['clicks'].mean() )
clicks_missing

Now, calculate the RMSE scores:

_ = rmse_score( clicks_original,
                clicks_missing,
                'clicks'
              )

Interestingly, for the Clickstream dataset, the mean imputation had the lowest RMSE score, in contrast to the results from the CO2 dataset.

date_clicks=clicks_missing[clicks_missing['clicks'].isnull()][[clicks_missing.columns[0],
                                                               'clicks'
                                                              ]]
median_x=[]
median_y=[]
for a in group_consecutive( date_clicks.index.to_list() ):
    median_idx=( a[0]+a[-1] )/2
    #print(clicks_missing[clicks_missing.index==a[0]-1].values[0][[0,3]])
    year,last_co2= clicks_missing[clicks_missing.index==a[0]-1].values[0][[0,3]]
    year,next_co2= clicks_missing[clicks_missing.index==a[-1]+1].values[0][[0,3]]
    median_co2 = ( last_co2 + next_co2)/2
    #print(last_co2, next_co2)
    median_x.append(median_idx)
    median_y.append(median_co2)
    
print(median_x)
print(median_y)

Let's visualize the results to get another perspective on performance:

plot_dfs( clicks_original,
          clicks_missing,
          'clicks',
          xlabel='date',
        )

You get the plots as follows:

Figure 7.10–Comparison between the three imputation methods for the Clickstream DataFrame

Compare the results in Figure 7.10 with the original data in Figure 7.8. Notice that from imputing two different datasets (CO2 and Clickstream), there is no one-size-fits-all strategy没有放之四海而皆准的策略 when it comes to handling missing data. Instead, each dataset requires a different strategy. Therefore, you should always inspect your results and align the outputs with the expectations based on the nature of your data.

There is a convenient shortcut for forward filling and backward filling in pandas. For example, instead of using DataFrame.fillna(method="ffill") , you can use DataFrame.ffill() . The same applies to bfill as well. The following shows how this can be implemented:

co2_missing['co2'].ffill()
co2_missing['co2'].bfill()

clicks_missing['clicks'].ffill()
clicks_missing["date"]=pd.to_datetime( clicks_missing["date"] )
clicks_missing.set_index(['date'])['clicks'].bfill()

Note I change datetime format

These shortcuts can be convenient when testing different imputation strategies.

To learn more about DataFrame.fillna() , please visit the official documentation page here: pandas.DataFrame.fillna — pandas 1.5.2 documentation

In the following recipe, you will perform similar univariate imputation, but this time using the scikit-learn library.

Handling missing data with univariate imputation using scikit-learn

scikit-learn is a very popular machine learning library in Python. The scikit-learn library offers a plethora/ˈpleθərə/过多,过剩 of options for everyday machine learning tasks and algorithms such as classification, regression, clustering, dimensionality reduction, model selection, and preprocessing.

Additionally, the library offers multiple options for univariate and multivariate data imputation.

1. You will be using the SimpleImputer class from the scikit-learn library to perform univariate imputation:

folder = 'https://raw.githubusercontent.com/PacktPublishing/Time-Series-Analysis-with-Python-Cookbook/main/datasets/Ch7'

co2_original = pd.read_csv( folder + '/co2_original.csv', 
                            #index_col='year',
                            parse_dates=['year']
                          )
co2_missing = pd.read_csv( folder + '/co2_missing_only.csv',
                           #index_col='year',
                           parse_dates=['year']
                         )

clicks_original = pd.read_csv( folder + '/clicks_original.csv',
                               #index_col='date',
                               parse_dates=['date']
                             )
clicks_missing = pd.read_csv( folder + '/clicks_missing.csv',
                              #index_col='date',
                              parse_dates=['date']
                            )
clicks_missing

co2_missing

2. SimpleImputer accepts different values for the strategy parameter, including mean, median, and most_frequent. Let's explore all three strategies and see how they compare. Create a list of tuples for each method:

strategy = [ ('Mean Strategy', 'mean'),
             ('Median Strategy', 'median'),
             ('Most Frequent Strategy', 'most_frequent')
           ]

You can loop through the Strategy list to apply the different imputation strategies. SimpleImputer has a fit_transform method. It combines two steps into one: fitting to the data ( .fit ), and then transforming the data ( .transform ).

Keep in mind that SimpleImputer accepts a NumPy array, so you will need to use the Series. values property followed by the .reshape(-1, 1) method to create a 2D NumPy array. Simply, what this is doing is transforming the 1D array from .values of shape (226, ) to a 2D array of shape (226, 1) , which is a column vector:

sklearn.impute.SimpleImputer — scikit-learn 1.2.0 documentation

class sklearn.impute.SimpleImputer(*, missing_values=nan, strategy='mean', fill_value=None, 
                                   verbose='deprecated', copy=True, add_indicator=False, 
                                   keep_empty_features=False
                                  )

SimpleImputer provides basic strategies that may be suitable with some data but not others. The advantage of these simple imputation strategies (including the ones from the previous Handling missing data with univariate imputation using pandas) recipe is that they are fast and straightforward to implement.

You used the SimpleImputer class to implement three simple strategies to impute missing values: mean, median, and most frequent (mode).

This is a univariate imputation technique, meaning only one feature or column was used to compute the mean, median, and most frequent value.

The SimpleImputer class has three parameters that you need to know:

missing_values int, float, str, np.nan, None or pandas.NA, default=np.nan

The placeholder for the missing values. All occurrences of missing_values will be imputed. For pandas’ dataframes with nullable integer dtypes with missing values, missing_values can be set to either np.nan or pd.NA.

SimpleImputer will impute all occurrences of the missing_values, which you can update with pandas.NA , an integer, float, or a string value.

strategy str, default=’mean’

The imputation strategy.

If “mean”, then replace missing values using the mean along each column. Can only be used with numeric data.
If “median”, then replace missing values using the median along each column. Can only be used with numeric data.
If “most_frequent”, then replace missing using the most frequent value along each column. Can be used with strings or numeric data. If there is more than one such value, only the smallest is returned.
If “constant”, then replace missing values with fill_value. Can be used with strings or numeric data.

fill_value str or numerical value, default=None

When strategy == “constant”, fill_value with a specifc value is used to replace all occurrences of missing_values. For string or object data types, fill_value must be a string. If None, fill_value will be 0 when imputing numerical data and “missing_value” for strings or object data types.

from sklearn.impute import SimpleImputer

co2_vals = co2_missing['co2'].values.reshape(-1,1)
clicks_vals = clicks_missing['clicks'].values.reshape(-1,1)

for s_name, s in strategy:
    co2_missing[s_name] = ( SimpleImputer(strategy=s).fit_transform(co2_vals) )
    clicks_missing[s_name] = ( SimpleImputer(strategy=s).fit_transform(clicks_vals) )

Now, both the clicks_missing and co2_missing DataFrames have three additional columns, one for each of the imputation strategies implemented.

3. Using the rmse_score function, you can now evaluate each strategy. Start with the CO2 data. You should get an output like the following:

_ = rmse_score( co2_original, co2_missing, 'co2' )

For the Clickstream data, you should get an output like the following:

_ = rmse_score( clicks_original, clicks_missing, 'clicks' )

Notice how the RMSE strategy rankings vary between the two datasets. For example, the Mean strategy performed best on the CO2 data, while the Median strategy did best on the Clickstream data.

#co2_missing.reset_index(inplace=True)
year_co2=co2_missing[co2_missing[co2_missing.columns[1]].isnull()][[co2_missing.columns[0],
                                                                    co2_missing.columns[1]
                                                                   ]]
median_x=[]
median_y=[]
for a in group_consecutive( year_co2.index.to_list() ):
    median_idx=( a[0]+a[-1] )/2
    year, last_co2= co2_missing[co2_missing.index==a[0]-1].iloc[:, 0:2].values[0]
    year, next_co2= co2_missing[co2_missing.index==a[-1]+1].iloc[:, 0:2].values[0]
    median_co2 = ( last_co2 + next_co2)/2
    #print(last_co2, next_co2)
    median_x.append(median_idx)
    median_y.append(median_co2)
    
print(median_x)
print(median_y)

4. Finally, use the plot_dfs function to plot the results. Start with the CO2 dataset:

plot_dfs( co2_original, co2_missing, 'co2', xlabel='year' )

Figure 7.11 – Comparing three SimpleImputer strategies for the CO2 dataset

Compare the results in Figure 7.11 with the original data in Figure 7.7.

For the Clickstream dataset, you should use the following:

date_clicks=clicks_missing[clicks_missing['clicks'].isnull()][[clicks_missing.columns[0],
                                                               'clicks'
                                                              ]]
median_x=[]
median_y=[]
for a in group_consecutive( date_clicks.index.to_list() ):
    median_idx=( a[0]+a[-1] )/2
    #print(clicks_missing[clicks_missing.index==a[0]-1].values[0][[0,3]])
    year,last_co2= clicks_missing[clicks_missing.index==a[0]-1].values[0][[0,3]]
    year,next_co2= clicks_missing[clicks_missing.index==a[-1]+1].values[0][[0,3]]
    median_co2 = ( last_co2 + next_co2)/2
    #print(last_co2, next_co2)
    median_x.append(median_idx)
    median_y.append(median_co2)
    
print(median_x)
print(median_y)

plot_dfs( clicks_original, clicks_missing, 'clicks', xlabel='date' )

Figure 7.12 – Comparing three SimpleImputer strategies for the Clickstream dataset

The pandas DataFrame, .fillna() , can provide the same functionality as SimpleImputer . For example, the mean strategy can be accomplished by using the pandas DataFrame.mean() method and passing to .fillna() .

The following example illustrates this:

avg = co2_missing['co2'].mean()
co2_missing['pandas_fillna_avg'] = co2_missing['co2'].fillna(avg)

cols = ['co2', 'Mean Strategy', 'pandas_fillna_avg']
_ = rmse_score(co2_original, co2_missing[cols], 'co2')

Notice how you were able to accomplish the same results as the SimpleImputer class from scikit-learn. The .fillna() method makes it easier to scale the imputation across the entire DataFrame (column by column). For example, if you have a sales_report_data DataFrame with multiple columns containing missing data, you can perform a mean imputation with a single line, sales_report_data.fillna( sales_report_data.mean() ) .

To learn more about scikit-learn's SimpleImputer class, please visit the official documentation page here: sklearn.impute.SimpleImputer — scikit-learn 1.2.0 documentation.

So far, you have been dealing with univariate imputation. A more powerful approach is multivariate imputation, which you will learn in the following recipe.

Handling missing data with multivariate imputation

Earlier, we discussed the fact that there are two approaches to imputing missing data: univariate imputation and multivariate imputation.

As you have seen in the previous recipes, univariate imputation involves using one variable (column) to substitute for the missing data, disregarding other variables in the dataset. Univariate imputation techniques are usually faster and simpler to implement, but a multivariate approach may produce better results in most situations.

Instead of using a single variable (column), in a multivariate imputation, the method uses multiple variables within the dataset to impute missing values. The idea is simple: Have more variables within the dataset chime/tʃaɪm/协调,一致 in to improve the predictability of missing values.

In other words, univariate imputation methods handle missing values for a particular variable in isolation of the entire dataset and just focus on that variable to derive the estimates. In multivariate imputation, the assumption is that there is some synergy/ˈsɪnərdʒi/协同增效作用,协同作用 within the variables in the dataset, and collectively集体地,共同地, they can provide better estimates to fill in for the missing values.

In this recipe, you will be working with the Clickstream dataset since it has additional variables (clicks, price, and location columns) to perform multivariate imputation for clicks.

In this recipe, you will use scikit-learn for the multivariate imputation. The library provides the IterativeImputer class, which allows you to pass a regressor to predict the missing values from other variables (columns) within the dataset:

1. Start by importing the necessary libraries, methods, and classes:

from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer
from sklearn.ensemble import ExtraTreesRegressor, BaggingRegressor
from sklearn.linear_model import ElasticNet, LinearRegression, BayesianRidge
from sklearn.neighbors import KNeighborsRegressor

Load the two Clickstream datasets into DataFrames:

clicks_original = pd.read_csv( folder + '/clicks_original.csv',
                               index_col='date', ######
                               parse_dates=['date']
                             )
clicks_missing = pd.read_csv( folder + '/clicks_missing.csv',
                              index_col='date', ######
                              parse_dates=['date']
                            )

One thing to note is that the interpolations use numerical values for the index.

##########################################################

07_Ensemble Learning and Random Forests_Bagging_Out-of-Bag_Random Forests_Extra-Trees极端随机树_Boosting_LIQING LIN的博客-CSDN博客

Bagging and Pasting

One way to get a diverse set of classifiers is to use 1.very different training algorithms, as just discussed. Another approach is to use the same training algorithm for every predictor, but to 2.train them on different random subsets of the training set. When sampling is performed with replacement, this method is called bagging装袋法(short for bootstrap aggregating自助法聚合. When sampling is performed without replacement, it is called pasting.
In other words, both bagging and pasting allow training instances to be sampled several times across multiple predictors, but only bagging allows training instances to be sampled several times for the same predictor. This sampling and training process is represented in Figure 7-4.
Figure 7-4. Pasting/bagging training set sampling and training

Once all predictors are trained, the ensemble can make a prediction for a new instance by simply aggregating the predictions of all predictors. The aggregation function is typically the statistical mode (i.e., the most frequent prediction, just like a hard voting classifier: to aggregate the predictions of each classifier and predict the class that gets the most votes.) for classification, or the average for regression. Each individual predictor has a higher bias than if it were trained on the original training set, but aggregation reduces both bias and variance. Generally, the net result is that the ensemble has a similar bias but a lower variance than a single predictor trained on the original training set. In other words, the bagging algorithm can be an effective approach to reducing the variance(too high variance~overfitting) of a model. However, bagging is ineffective in reducing model bias, that is, models that are too simple to capture the trend in the data well. This is why we want to perform bagging on an ensemble of classifiers with low bias, for example, unpruned decision trees.Figure 7-5. A single Decision Tree versus a bagging ensemble of 500 trees

As you can see in Figure 7-4, predictors can all be trained in parallel, via different CPU cores or even different servers. Similarly, predictions can be made in parallel. This is one of the reasons why bagging and pasting are such popular methods: they scale可扩展性 very well.
######################################
NOTE
The BaggingClassifier automatically performs soft voting instead of hard voting if the base classifier can estimate class probabilities (i.e., if it has a predict_proba() method), which is the case with Decision Trees classifiers.
######################################

Extra-Trees

When you are growing a tree in a Random Forest, at each node only a random subset of the features is considered for splitting (as discussed earlier). It is possible to make trees even more random by also using random thresholds for each feature rather than searching for the best possible thresholds (like regular Decision Trees do).

The random forest algorithm can be summarized in four simple steps:

1. Draw a random bootstrap sample of size n (randomly choose n samples from the training set with replacement).
2. Grow a decision tree from the bootstrap sample. At each node:
- a. Randomly select d features without replacement.
- b. Split the node using the feature that provides the best split according to the objective function, for instance, maximizing the information gain.
3. Repeat the steps 1-2 k times.
4. Aggregate the prediction by each tree to assign the class label by majority vote. Majority voting will be discussed in more detail in Chapter 7, Combining Different Models for Ensemble Learning.

We should note one slight modification in step 2 when we are training the individual decision trees: instead of evaluating all features to determine the best split at each node, we only consider a random subset of those.

A forest of such extremely random trees is simply called an Extremely Randomized Trees ensemble 极端随机树(or Extra-Trees for short). Once again, this trades more bias for a lower variance. It also makes Extra-Trees much faster to train than regular Random Forests since finding the best possible threshold for each feature at every node is one of the most time-consuming tasks of growing a tree
##############################
mpf9_Backtesting_mean-reverting_threshold_model_Survivorship bias_sklearn打印默认参数_Gini_k-mean_knn_CART_LIQING LIN的博客-CSDN博客_sklearn中knn打印参数

We start with a dataset at the parent node that consists of 40 samples from class 1 and 40 samples from class 2 that we split into two datasets and , respectively.

(Gini impurity=1 – Gini) would favor the split in scenario A() over scenario B(), which is indeed more pure:
vs

for each split, we will calculate the Gini impurities and the split producing minimum Gini impurity() will be selected as the split. And you know, that the minimum value of Gini impurity means that the node will be purer and more homogeneous更均匀.

Equation 6-1. Gini impurity<=
is the ratio of class k instances among the training instances in thenode/region.
probabilities: 0% for Iris-Setosa (0/54), 90.7% for Iris-Versicolor (49/54), and 9.3% for Iris-Virginica (5/54)
<0.5 #A node's Gini impurity is generally lower than its parent's(0.5).
=0.02119230769230769230769230769231
##############################
(step 2b: Extra-Trees use random thresholds for each feature. This extra randomness acts like a form of regularization: if a Random Forest overfits the training data, Extra-Trees might perform better).

You can create an Extra-Trees classifier using Scikit-Learn's ExtraTreesClassifier class. Its API is identical to the RandomForestClassifier class. Similarly, the Extra TreesRegressor class has the same API as the RandomForestRegressor class.
#############################
TIP
It is hard to tell in advance whether a RandomForestClassifier will perform better or worse than an ExtraTreesClassifier.
Generally, the only way to know is to try both and compare them using cross-validation (and tuning the hyperparameters using grid search).
#############################04_TrainingModels_02_regularization_L2_cost_Ridge_Lasso_Elastic Net_Early Stopping_LIQING LIN的博客-CSDN博客

Elastic Net

Equation 4-8. Ridge Regression cost function
vs
use RSS(Residuals of Sum Squares) instead of MSE
$\frac{1}{2}$ is for convenient computation, , we should remove it for Practical application
For Gradient Descent, just add 2αw to the MSE gradient vector (Equation 4-6)
+2αw (or +2α)

Equation 4-9. Ridge Regression closed-form solution 04_TrainingModels_Normal Equation(正态方程,正规方程) Derivation_Gradient Descent_Polynomial Regression_LIQING LIN的博客-CSDN博客
Note: Normal Equation(a closed-form equation)

Equation 4-10. Lasso Regression cost function
vs
use RSS(Residuals of Sum Squares) instead of MSE
Elastic Net is a middle ground between Ridge Regression and Lasso Regression. The regularization term is a simple mix of both Ridge and Lasso’s regularization terms, and you can control the mix ratio r. When r = 0, Elastic Net is equivalent to Ridge Regression, and when r = 1, it is equivalent to Lasso Regression (see Equation 4-12).
Equation 4-12. Elastic Net cost function

L1 norm: e.g.
L2 norm: sqrt( ) e.g.

class sklearn.linear_model.ElasticNet(alpha=1.0, *, l1_ratio=0.5, fit_intercept=True, 
                                      precompute=False, max_iter=1000, copy_X=True, 
                                      tol=0.0001, warm_start=False, positive=False, 
                                      random_state=None, selection='cyclic'
                                     )

Minimizes the objective function: $\frac{1}{2}$ is for convenient computation in 1 / (2 * n_samples)

1 / (2 * n_samples) * ||y - Xw||^2_2
+ alpha * l1_ratio * ||w||_1
+ 0.5 * alpha * (1 - l1_ratio) * ||w||^2_2

##########################################################

2. With IterativeImputer, you can test different estimators. So, let's try different regressors and compare the results. Create a list of the regressors (estimators) to be used in IterativeImputer :

estimators = [ ( 'bagging', BaggingRegressor(n_estimators=10) ), # ensemble of 500 Decision Tree
               ( 'extra_trees', ExtraTreesRegressor(n_estimators=10) ), # Extremely Randomized Trees ensemble
               ( 'elastic_net', ElasticNet() ),
               ( 'bayesianRidge', BayesianRidge() ),
               ( 'linear_regression', LinearRegression() ),
               ( 'knn', KNeighborsRegressor(n_neighbors=3) )
             ]

class sklearn.impute.IterativeImputer(estimator=None, *, missing_values=nan, 
                                      sample_posterior=False, max_iter=10, tol=0.001, 
                                      n_nearest_features=None, initial_strategy='mean', 
                                      imputation_order='ascending', skip_complete=False, 
                                      min_value=-inf, max_value=inf, verbose=0, 
                                      random_state=None, add_indicator=False, 
                                      keep_empty_features=False
                                     )

3. Loop through the estimators and train on the dataset using .fit() , thereby building different models, and finally apply the imputation using .transform() on the variable with missing data. The results of each estimator will be appended as a new column to the clicks_missing DataFrame so that it can be used for scoring and compare the results visually:

clicks_missing.iloc[:,1:4]

#price	location	clicks
clicks_vals = clicks_missing.iloc[:,0:3].values #clicks_missing.iloc[:,1:4].values

for e_name, e in estimators:
    est = IterativeImputer( random_state=15,
                            estimator=e
                          ).fit(clicks_vals)
    clicks_missing[e_name] = est.transform(clicks_vals)[:, 2]# the index of 'clicks' : 2

4. Using the rmse_score function, evaluate each estimator:

_ = rmse_score(clicks_original, clicks_missing, 'clicks')

clicks_original.reset_index(inplace=True)

clicks_missing.reset_index(inplace=True)
clicks_missing

Observe that Bayesian Ridge, ElasticNet, and Linear Regression produce similar results.

import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
from matplotlib.dates import DateFormatter

def plot_dfs( df1, df2, col, title=None, xlabel=None, ylabel=None, offset=0.5 ):
    '''
    df1: original dataframe without missing data
    df2: dataframe with missing data
    col: column name that contains missing data
    '''
    m='missing'
    df_missing = df2.rename( columns={col: m} )
    
    columns = df_missing.loc[:, 'missing':].columns.tolist()
    # .columns : Index(['missing'], dtype='object')
    subplots_size = len( columns )
    
    # subplots_size = df2.shape[1]
    fig, ax = plt.subplots( subplots_size+1, 1, sharex = True,
                            figsize=(10,11)
                          )
    plt.subplots_adjust( hspace=0.3 )
    fig.suptitle(title, y=0.92)
    
    #print(np.array( df1[df1.columns[0]].values,))# df1['year'].values
#    df1[col].plot( ax=ax[0] )
    ax[0].plot( np.array( df1[df1.columns[0]].values,),
                df1[col].values,
              )
    
    ax[0].set_title( r'$\bf{Original Dataset}$' )
    ax[0].set_ylabel( ylabel )
    ax[0].autoscale(enable=True, axis='x', tight=True)### ### Align both ends

    #missing
    for i, columnName in enumerate( columns ):
        #df_missing[columnName].plot( ax=ax[i+1] )  # columnName.capitalize()
        ax[i+1].plot( np.array( df_missing[df_missing.columns[0]].values,),
                      df_missing[columnName].values,
                    )
        ax[i+1].set_title( r'$\bf{}$'.format( columnName.upper() ) )

        if columnName == m:
            for j in range( len(median_x) ):
                ax[i+1].annotate('',#str(median_x[j]),
                                 ha='center', va='center',
                                 xy= (df_missing[df_missing.index==int(median_x[j])][df_missing.columns[0]], 
                                      median_y[j],
                                     ),
                                 xytext=(df_missing[df_missing.index==int(median_x[j])][df_missing.columns[0]],
                                         median_y[j]+offset
                                        ),
                                 arrowprops=dict(arrowstyle='->, head_width=0.5, head_length=0.8',
                                                 facecolor='red',ls="-",
                                                 linewidth=3, edgecolor='red',
                                                )
                                )
        ax[i+1].autoscale(enable=True, axis='x', tight=True)### ### Align both ends     
    ax[-1].set_xlabel( xlabel )
    ax[-1].xaxis.set_major_locator(ticker.MaxNLocator(12))  
    ax[-1].xaxis.set_major_formatter( DateFormatter('%Y-%m') ) # 2015-08-30 ==> 2015-08
    plt.setp( ax[-1].get_xticklabels(), rotation=45, horizontalalignment='right', fontsize=10 )
    
    plt.show()

5. Finally, plot the results for a visual comparison between the best three:

plot_dfs( clicks_original, clicks_missing, 'clicks', xlabel='date' )

Figure 7.13 – Comparing diferent estimators using IterativeImputation

Compare the results in Figure 7.13 with the original data in Figure 7.8.

Early in the chapter, we noted that the RMSE could be misleading because we did not seek the best score (smallest value) since we are not scoring a prediction model but rather an imputation model to fill for missing data. Later, you may use the data (with imputed values) to build another model for making predictions (forecasting). Thus, we do not mind some imperfections缺陷 to better resemble real data. Additionally, since we may not know the true nature of the missing data, the goal is to get a decent estimate目标是获得一个合理的估计. For example, the three with the lowest RMSE scores (BayesianRidge, ElasticNet, and Linear Regression) did not capture some of the randomness in the data.

The R MICE package inspired the IterativeImputer class from the scikit-learn library to implement Multivariate Imputation by Chained Equation ( https://www.jstatsoft.org/article/download/v045i03/550). IterativeImputer does differ
from the original implementation, which you can read more about here: 6.4. Imputation of missing values — scikit-learn 1.2.0 documentation .

Keep in mind that IterativeImputer is still in experimental mode. In the next section, you will use another implementation of MICE from the statsmodels library.

6.4. Imputation of missing values

For various reasons, many real world datasets contain missing values, often encoded as blanks, NaNs or other placeholders. Such datasets however are incompatible with scikit-learn estimators which assume that all values in an array are numerical, and that all have and hold meaning. A basic strategy to use incomplete datasets is to discard entire rows and/or columns containing missing values. However, this comes at the price of losing data which may be valuable (even though incomplete). A better strategy is to impute the missing values, i.e., to infer them from the known part of the data. See the glossary entry on imputation(Most machine learning algorithms require that their inputs have no missing values, and will not work if this requirement is violated. Algorithms that attempt to fill in (or impute) missing values are referred to as imputation algorithms).

6.4.1. Univariate vs. Multivariate Imputation

One type of imputation algorithm is univariate, which imputes values in the i-th feature dimension using only non-missing values in that feature dimension (e.g. impute.SimpleImputer). By contrast, multivariate imputation algorithms use the entire set of available feature dimensions to estimate the missing values (e.g. impute.IterativeImputer).

6.4.2. Univariate feature imputation

The SimpleImputer class provides basic strategies for imputing missing values. Missing values can be imputed with a provided constant value, or using the statistics (mean, median or most frequent) of each column in which the missing values are located. This class also allows for different missing values encodings.

The following snippet demonstrates how to replace missing values, encoded as np.nan, using the mean value of the columns (axis 0) that contain the missing values:

import numpy as np
from sklearn.impute import SimpleImputer

x_0 = [[1, 2], 
       [np.nan, 3], 
       [7, 6],
      ]# mean [(1+7)/2=4,  (2+3+6)/3=3.66666667]

imp = SimpleImputer(missing_values=np.nan, strategy='mean')
imp.fit(x_0)

==>

X = [[np.nan, 2], 
     [6, np.nan], 
     [7, 6]
    ]
print( imp.transform(X) )

The SimpleImputer class also supports sparse matrices:

import scipy.sparse as sp

X = sp.csc_matrix([[1, 2], 
                   [0, -1], 
                   [8, 4]
                  ])# mean [(1+8)/3=3,  (2+4)/2=3]
imp = SimpleImputer(missing_values=-1, strategy='mean')
imp.fit(X)

X_test = sp.csc_matrix([[-1, 2], 
                        [6, -1], 
                        [7, 6]
                       ])
print( imp.transform(X_test).toarray() )

Note that this format is not meant to be used to implicitly store missing values in the matrix because it would densify加密 it at transform time. Missing values encoded by 0 must be used with dense input.

The SimpleImputer class also supports categorical data represented as string values or pandas categoricals when using the 'most_frequent' or 'constant' strategy:

import pandas as pd
df = pd.DataFrame([["a", "x"],
                   [np.nan, "y"],
                   ["a", np.nan],
                   ["b", "y"]
                  ], 
                  dtype="category"
                 )

imp = SimpleImputer(strategy="most_frequent")
print( imp.fit_transform(df) )

6.4.3. Multivariate feature imputation

A more sophisticated approach is to use the IterativeImputer class, which models each feature with missing values as a function of other features, and uses that estimate for imputation. It does so in an iterated round-robin fashion: at each step, a feature column is designated as output y and the other feature columns are treated as inputs X. A regressor is fit on (X,y) for known y. Then, the regressor is used to predict the missing values of y. This is done for each feature in an iterative fashion, and then is repeated for max_iter imputation rounds. The results of the final imputation round are returned.

Note

This estimator is still experimental for now: default parameters or details of behaviour might change without any deprecation cycle. Resolving the following issues would help stabilize IterativeImputer: convergence criteria (#14338), default estimators (#13286), and use of random state (#15611). To use it, you need to explicitly import enable_iterative_imputer.

import numpy as np
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer

imp = IterativeImputer(max_iter=10, random_state=0)
imp.fit_transform([[1, 2], 
                   [3, 6], 
                   [4, 8], 
                   [np.nan, 3], 
                   [7, np.nan]
                  ])

X_test = [[np.nan, 2], 
          [6, np.nan],
          [np.nan, 6]
         ]
# the model learns that the second feature is double the first
print(np.round( imp.transform(X_test) ))

Both SimpleImputer and IterativeImputer can be used in a Pipeline as a way to build a composite estimator that supports imputation. See Imputing missing values before building an estimator.

6.4.3.1. Flexibility of IterativeImputer

There are many well-established imputation packages in the R data science ecosystem: Amelia, mi, mice, missForest, etc. missForest is popular, and turns out to be a particular instance of different sequential imputation algorithms that can all be implemented with IterativeImputer by passing in different regressors to be used for predicting missing feature values. In the case of missForest, this regressor is a Random Forest. See Imputing missing values with variants of IterativeImputer.

6.4.3.2. Multiple vs. Single Imputation

In the statistics community, it is common practice to perform multiple imputations, generating, for example, m separate imputations for a single feature matrix. Each of these m imputations is then put through the subsequent analysis pipeline (e.g. feature engineering, clustering, regression, classification). The m final analysis results (e.g. held-out validation errors) allow the data scientist to obtain understanding of how analytic results may differ as a consequence of the inherent固有 uncertainty caused by the missing values. The above practice is called multiple imputation.

Our implementation of IterativeImputer was inspired by the R MICE package (Multivariate Imputation by Chained Equations) [1], but differs from it by returning a single imputation instead of multiple imputations. However, IterativeImputer can also be used for multiple imputations by applying it repeatedly to the same dataset with different random seeds when sample_posterior=True. See [2], chapter 4 for more discussion on multiple vs. single imputations.

It is still an open problem as to how useful single vs. multiple imputation is in the context of prediction and classification when the user is not interested in measuring uncertainty due to missing values.

Note that a call to the transform method of IterativeImputer is not allowed to change the number of samples. Therefore multiple imputations cannot be achieved by a single call to transform.

6.4.4. Nearest neighbors imputation

The KNNImputer class provides imputation for filling in missing values using the k-Nearest Neighbors approach. By default, a euclidean distance metric that supports missing values, nan_euclidean_distances, is used to find the nearest neighbors. Each missing feature is imputed using values from n_neighbors nearest neighbors that have a value for the feature. The feature of the neighbors are averaged uniformly or weighted by distance to each neighbor. If a sample has more than one feature missing, then the neighbors for that sample can be different depending on the particular feature being imputed. When the number of available neighbors is less than n_neighbors and there are no defined distances to the training set, the training set average for that feature is used during imputation.

If there is at least one neighbor with a defined distance, the weighted or unweighted average of the remaining neighbors will be used during imputation.
If a feature is always missing in training, it is removed during transform.
For more information on the methodology, see ref. [OL2001].

The following snippet demonstrates how to replace missing values, encoded as np.nan, using the mean feature value of the two nearest neighbors of samples with missing values:

import numpy as np
from sklearn.impute import KNNImputer

nan = np.nan
X = [[1, 2, nan], 
     [3, 4, 3], 
     [nan, 6, 5], 
     [8, 8, 7]
    ]
imputer = KNNImputer( n_neighbors=2, 
                      weights="uniform"
                    )
imputer.fit_transform(X)

array([[1. , 2. , 4. ],
[3. , 4. , 3. ],
[5.5, 6. , 5. ],
[8. , 8. , 7. ]
])

6.4.5. Keeping the number of features constants

By default, the scikit-learn imputers will drop fully empty features, i.e. columns containing only missing values. For instance:

imputer = SimpleImputer()
X = np.array([[np.nan, 1], 
              [np.nan, 2], 
              [np.nan, 3]
             ])
imputer.fit_transform(X)

The first feature in X containing only np.nan was dropped after the imputation. While this feature will not help in predictive setting, dropping the columns will change the shape of X which could be problematic when using imputers in a more complex machine-learning pipeline. The parameter keep_empty_features offers the option to keep the empty features by imputing with a constant values. In most of the cases, this constant value is zero:

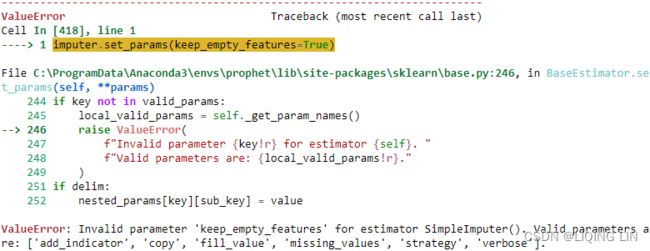
imputer.set_params(keep_empty_features=True)

ValueError: Invalid parameter 'keep_empty_features' for estimator SimpleImputer()

solution:

imputer.set_params(strategy='constant', fill_value=0)

imputer.fit_transform(X)

6.4.6. Marking imputed values

The MissingIndicator transformer is useful to transform a dataset into corresponding binary matrix indicating the presence of missing values in the dataset. This transformation is useful in conjunction with imputation. When using imputation, preserving the information about which values had been missing can be informative. Note that both the SimpleImputer and IterativeImputer have the boolean parameter add_indicator (False by default) which when set to True provides a convenient way of stacking the output of the MissingIndicator transformer with the output of the imputer.

NaN is usually used as the placeholder for missing values. However, it enforces the data type to be float. The parameter missing_values allows to specify other placeholder such as integer. In the following example, we will use -1 as missing values:

from sklearn.impute import MissingIndicator

X = np.array([[-1, -1, 1, 3],
              [4, -1, 0, -1],
              [8, -1, 1, 0]])
indicator = MissingIndicator(missing_values=-1)
mask_missing_values_only = indicator.fit_transform(X)
mask_missing_values_only

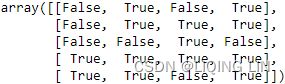
The features parameter is used to choose the features for which the mask is constructed. By default, it is 'missing-only' which returns the imputer mask of the features containing missing values at fit time:

indicator.features_

indicator.get_feature_names_out()

The features parameter can be set to 'all' to return all features whether or not they contain missing values:

indicator = MissingIndicator(missing_values=-1, features='all')
mask_all = indicator.fit_transform(X)
mask_all

indicator.features_

indicator.get_feature_names_out()

When using the MissingIndicator in a Pipeline, be sure to use the FeatureUnion or ColumnTransformer to add the indicator features to the regular features. First we obtain the iris dataset, and add some missing values to it.

from sklearn.datasets import load_iris
from sklearn.impute import SimpleImputer, MissingIndicator
from sklearn.model_selection import train_test_split
from sklearn.pipeline import FeatureUnion, make_pipeline
from sklearn.tree import DecisionTreeClassifier

X, y = load_iris(return_X_y=True)
X[:5]

y[:5]

mask = np.random.randint(0, 2, size=X.shape).astype(bool)
mask[:5]

train_test_split(X, y, test_size=100,
                 random_state=0
                )[1][:5]

the actual X_test

X[mask] = np.nan
X_train, X_test, y_train, _ = train_test_split(X, y, test_size=100,
                                               random_state=0
                                              )
X_test[:5]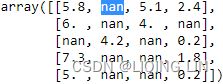

<==
Now we create a FeatureUnion. All features will be imputed using SimpleImputer, in order to enable classifiers to work with this data. Additionally, it adds the indicator variables from MissingIndicator.

transformer = FeatureUnion( transformer_list=[ ( 'features', SimpleImputer(strategy='mean') ),
                                               ( 'indicators', MissingIndicator() )
                                             ]
                          )
transformer = transformer.fit(X_train, y_train)
results = transformer.transform(X_test)
results.shape

results[:5]

+indicator: 0, 1, 0, 0 ~

transformer.transformer_list

transformer.transformer_list[1][1].features_

transformer.transformer_list[1][1].get_feature_names_out()

Of course, we cannot use the transformer to make any predictions. We should wrap this in a Pipeline with a classifier (e.g., a DecisionTreeClassifier) to be able to make predictions.

clf = make_pipeline( transformer, 
                     DecisionTreeClassifier() # for make a prediction
                   )
clf = clf.fit(X_train, y_train)
results = clf.predict(X_test) # prediction

results.shape

6.4.7. Estimators that handle NaN values

Some estimators are designed to handle NaN values without preprocessing. Below is the list of these estimators, classified by type (cluster, regressor, classifier, transform):

Estimators that allow NaN values for type regressor:
- HistGradientBoostingRegressor
Estimators that allow NaN values for type classifier:
- HistGradientBoostingClassifier
Estimators that allow NaN values for type transformer:
- IterativeImputer
- KNNImputer
- MaxAbsScaler
- MinMaxScaler
- MissingIndicator
- PowerTransformer
- QuantileTransformer
- RobustScaler
- SimpleImputer
- StandardScaler
- VarianceThreshold

MICE(Multivariate Imputation by Chained Equation)

The statsmodels library has an implementation of MICE that you can test and compare with IterariveImputer . This implementation is closer to the MICE implementation in R.

class statsmodels.imputation.mice.MICEData(data, perturbation_method='gaussian', k_pmm=20,
                                           history_callback=None
                                          )

Wrap a data set to allow missing data handling with MICE.

Parameters:

data Pandas data frame

The data set, which is copied internally.

perturbation_method str

The default perturbation method默认扰动方法

k_pmm

The number of nearest neighbors to use during predictive mean matching. Can also be specified in fit.

history_callback function

A function that is called after each complete imputation cycle. The return value is appended to history. The MICEData object is passed as the sole argument to history_callback.

Notes

Allowed perturbation methods are ‘gaussian’ (the model parameters are set to a draw from the Gaussian approximation to the posterior distribution), and ‘boot’ (the model parameters are set to the estimated values obtained when fitting a bootstrapped version of the data set).

history_callback can be implemented to have side effects such as saving the current imputed data set to disk.

MICEData.set_imputer(endog_name, formula=None, model_class=None, init_kwds=None,
                     fit_kwds=None, predict_kwds=None, k_pmm=20, perturbation_method=None,
                     regularized=False
                    )

VAR is used when you have two or more time series that have (or are assumed to have) an influence on each other's behavior当您有两个或多个时间序列对彼此的行为产生影响（或被认为具有影响）时. These are normally referred to as endogenous variables内生变量 and the relationship is bi-directional. If the variables or time series are not directly related, or we do not know if there is a direct influence within the same system, we refer to them as exogenous variables外生变量.

You will use the same DataFrames ( clicks_original and clicks_missing ) and append the statsmodels MICE imputation output to the clicks_missing DataFrame as an additional column.

from statsmodels.imputation.mice import MICE, MICEData, MICEResults
import statsmodels.api as sm

clicks_missing.set_index('date', inplace=True)
clicks_missing

Since your goal is to impute missing data, you can use the MICEData class to wrap the clicks_missing DataFrame. Start by creating an instance of MICEData and store it in a mice_data variable:

# create a MICEData object
fltr = ['price', 'location', 'clicks']
mice_data = MICEData( clicks_missing[fltr],
                      perturbation_method='gaussian'
                    )
# Perform a specified number of MICE iterations : 20 iterations
mice_data.update_all( n_iter=20 ) # Only the result of the final update will be available.
# The imputed values are stored in the class attribute self.data.

# Specify the imputation process for a single variable.
# VAR is used when you have two or more time series that have (or are assumed to have) 
# an influence on each other's behavior
mice_data.set_imputer( endog_name='clicks', # Name of the variable to be imputed.
                       formula='~ price + location', 
                       model_class = sm.OLS # Conditional model for imputation 
                     )

clicks_missing['MICE'] = mice_data.data['clicks'].values.tolist()
clicks_missing.reset_index(inplace=True)
clicks_missing

Store the results in a new column and call it MICE. This way, you can compare the scores
with results from IterativeImputer :

# def rmse_score( df1, df2, col=None ):
#     '''
#     df1: original dataframe without missing data
#     df2: dataframe with missing data
#     col: column name that contains missing data
    
#     returns: a list of scores
#     '''
#     df_missing = df2.rename( columns={col: 'missing'} )
#     columns = df_missing.loc[:, 'missing':].columns.tolist() # co2, ffill, bfill, mean
#     scores = []
#     for comp_col in columns[1:]:
#         rmse = np.sqrt( np.mean( ( df1[col]-df_missing[comp_col] )**2 ) )
#         scores.append( rmse )
#         print( f'RMSE for {comp_col}: {rmse}' )
#     return scores

_ = rmse_score( clicks_original, clicks_missing, 'clicks')

Finally, visualize the results for a final comparison. This will include some of the imputations from IterativeImputer

cols = ['date','clicks','bayesianRidge', 'bagging', 'knn', 'MICE']
plot_dfs(clicks_original, clicks_missing[cols], 'clicks', xlabel='date')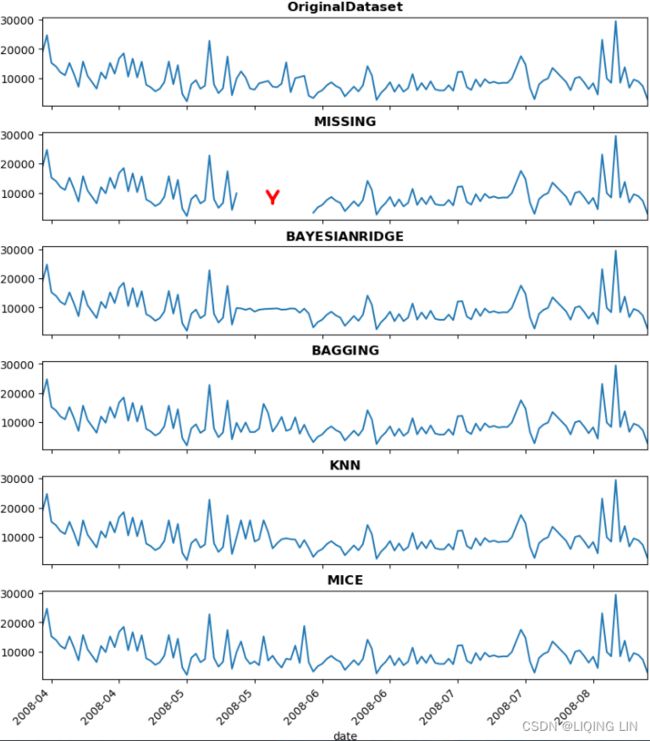

Figure 7.14–Comparing the statsmodels MICE implementation with the scikit-learn IterativeImputer

Compare the results in Figure 7.14 with the original data in Figure 7.8.

Overall, multivariate imputation techniques generally produce better results than univariate methods(see Original dataset plot VS MICE and univariate methods' plot). This is true when working with more complex time-series datasets in terms of the number of features (columns) and records. Though univariate imputers are more efficient in terms of speed and simplicity to interpret, there is a need to balance complexity, quality, and analytical requirements.

MICEData.plot_imputed_hist(col_name, ax=None, imp_hist_args=None, obs_hist_args=None,
                           all_hist_args=None
                          )

Display imputed values for one variable as a histogram.

col_name (string) – The name of the variable to be plotted.
ax (matplotlib axes) – An axes on which to draw the histograms. If not provided, one is created.
imp_hist_args (dict) – Keyword arguments to be passed to pyplot.hist when creating the histogram for imputed values.
obs_hist_args (dict) – Keyword arguments to be passed to pyplot.hist when creating the histogram for observed values.
all_hist_args (dict) – Keyword arguments to be passed to pyplot.hist when creating the histogram for all values.

_ = mice_data.plot_imputed_hist('clicks')

An interesting library, FancyImpute, that originally inspired scikit-learn's IterativeImputer offers a variety of imputation algorithms that you can check out here: GitHub - iskandr/fancyimpute: Multivariate imputation and matrix completion algorithms implemented in Python

MICEData.plot_fit_obs(col_name, lowess_args=None, lowess_min_n=40, jitter=None, 
                      plot_points=True, ax=None
                     )

Plot fitted versus imputed or observed values as a scatterplot.

Parameters:	col_name (string) – The variable to be plotted on the horizontal axis. lowess_args (dict-like) – Keyword arguments passed to lowess fit. A dictionary of dictionaries, keys are ‘o’ and ‘i’ denoting ‘observed’ and ‘imputed’, respectively. lowess_min_n (integer) – Minimum sample size to plot a lowess fit jitter (float or tuple) – Standard deviation for jittering points in the plot. Either a single scalar applied to both axes, or a tuple containing x-axis jitter and y-axis jitter, respectively. plot_points (bool) – If True, the data points are plotted. ax (matplotlib axes object) – Axes on which to plot, created if not provided.

Parameters:

col_name (string) – The variable to be plotted on the horizontal axis.
lowess_args (dict-like) – Keyword arguments passed to lowess fit. A dictionary of dictionaries, keys are ‘o’ and ‘i’ denoting ‘observed’ and ‘imputed’, respectively.
lowess_min_n (integer) – Minimum sample size to plot a lowess fit
jitter (float or tuple) – Standard deviation for jittering points in the plot. Either a single scalar applied to both axes, or a tuple containing x-axis jitter and y-axis jitter, respectively.
plot_points (bool) – If True, the data points are plotted.
ax (matplotlib axes object) – Axes on which to plot, created if not provided.

# # create a MICEData object
#fltr = ['price', 'location', 'clicks']
mice_data = MICEData(clicks_missing[fltr], 
                     perturbation_method='gaussian')
# # Perform a specified number of MICE iterations : 20 iterations
mice_data.update_all( n_iter=20 ) # Only the result of the final update will be available.
_ = mice_data.plot_fit_obs('clicks')

Handling missing data with interpolation

Another commonly used technique for imputing missing values is interpolation. The pandas library provides the DataFrame.interpolate() method for more complex univariate imputation strategies.

For example, one of the interpolation methods available is linear interpolation. Linear interpolation can be used to impute missing data by drawing a straight line between the two points surrounding the missing value (in time series, this means for a missing data point, it looks at a prior past value and the next future value to draw a line between them). A polynomial interpolation, on the other hand, will attempt to draw a curved line between the two points. Hence, each method will have a diferent mathematical operation to determine how to fill in for the missing data.

The interpolation capabilities in pandas can be extended further through the SciPy library, which ofers additional univariate and multivariate interpolations.

https://blog.csdn.net/Linli522362242/article/details/108745121

In this recipe, you will use the pandas DataFrame.interpolate() function to examine different interpolation methods, including linear, polynomial, quadratic, nearest, and spline.

You will perform multiple interpolations on two different datasets and then compare the results using RMSE and visualization:

1. Start by importing the libraries and reading the data into DataFrames:

folder = 'https://raw.githubusercontent.com/PacktPublishing/Time-Series-Analysis-with-Python-Cookbook/main/datasets/Ch7'

co2_original = pd.read_csv( folder + '/co2_original.csv', 
                            index_col='year',
                            parse_dates=['year']
                          )
co2_missing = pd.read_csv( folder + '/co2_missing_only.csv',
                           index_col='year',
                           parse_dates=['year']
                         )

clicks_original = pd.read_csv( folder + '/clicks_original.csv',
                               index_col='date',
                               parse_dates=['date']
                             )
clicks_missing = pd.read_csv( folder + '/clicks_missing.csv',
                              index_col='date',
                              parse_dates=['date']
                            )
co2_missing

One thing to note is that only linear interpolation ignores the index, while the rest use numerical values for the index.

co2_missing.interpolate()

2. Create a list of the interpolation methods to be tested: linear, quadratic, nearest, and cubic

interpolations = [ 'linear',
                   'quadratic',
                   'nearest',
                   'cubic'
                 ]

3. You will loop through the list to run different interpolations using .interpolate() . Append a new column for each interpolation output to be used for comparison:

for intp in interpolations:
    co2_missing[intp] = co2_missing['co2'].interpolate( method=intp )
    clicks_missing[intp] = clicks_missing['clicks'].interpolate( method=intp )

co2_missing.iloc[130:145]

clicks_missing.iloc[43:61]

4. There are two additional methods that it would be interesting to test: spline and polynomial. To use these methods, you will need to provide an integer value for the order parameter. You can try order = 2 for the spline method, and order = 5 for the polynomial method. For the spline method, for example, it would look like this: .interpolate(method="spline", order = 2) :

co2_missing['spline'] = co2_missing['co2'].interpolate( method='spline',
                                                        order=2
                                                      )
clicks_missing['spline'] = clicks_missing['clicks'].interpolate( method='spline',
                                                                 order=2
                                                               )
co2_missing['polynomial'] = co2_missing['co2'].interpolate( method='polynomial',
                                                            order=5
                                                          )
clicks_missing['polynomial'] = clicks_missing['clicks'].interpolate( method='polynomial',
                                                                     order=5
                                                                   )

co2_missing['spline3'] = co2_missing['co2'].interpolate( method='spline',
                                                         order=3
                                                       )
clicks_missing['spline3'] = clicks_missing['clicks'].interpolate( method='spline',
                                                                  order=3
                                                                )
co2_missing['polynomial3'] = co2_missing['co2'].interpolate( method='polynomial',
                                                             order=3
                                                           )
clicks_missing['polynomial3'] = clicks_missing['clicks'].interpolate( method='polynomial',
                                                                      order=3
                                                                    )
clicks_missing.iloc[43:61]

co2_missing.iloc[130:145]

5. Use the rmse_score function to compare the results from the different interpolation strategies. Start with CO2 data:

_ = rmse_score( co2_original, co2_missing, 'co2' )

Now, let's check the Clickstream data:

_ = rmse_score( clicks_original, clicks_missing, 'clicks' )

6. Lastly, visualize the results to gain a better idea of how each interpolation worked. Start with the CO2 dataset:

co2_original.reset_index(inplace=True)
co2_missing.reset_index(inplace=True)

year_co2=co2_missing[co2_missing[co2_missing.columns[1]].isnull()][[co2_missing.columns[0],
                                                                    co2_missing.columns[1]
                                                                   ]]
median_x=[]
median_y=[]
for a in group_consecutive( year_co2.index.to_list() ):
    median_idx=( a[0]+a[-1] )/2
    year, last_co2= co2_missing[co2_missing.index==a[0]-1].iloc[:, 0:2].values[0]
    year, next_co2= co2_missing[co2_missing.index==a[-1]+1].iloc[:, 0:2].values[0]
    median_co2 = ( last_co2 + next_co2)/2
    #print(last_co2, next_co2)
    median_x.append(median_idx)
    median_y.append(median_co2)
    
print(median_x)
print(median_y)

cols = ['year', 'co2', 'linear', 'nearest', 'polynomial', 'cubic']
plot_dfs(co2_original, co2_missing[cols], 'co2', xlabel='year')

Figure 7.15 – Comparing the different interpolation strategies on the CO2 dataset(polynomial order=5, better)

Compare the results in Figure 7.15 with the original data in Figure 7.7.

Both the linear and nearest methods seem to have a similar effect regarding how the missing values were imputed. This can be seen from the RMSE scores and plot.

Now, create the plots for the Clickstream dataset:

clicks_original.reset_index(inplace=True)
clicks_missing.reset_index(inplace=True)

date_clicks=clicks_missing[clicks_missing['clicks'].isnull()][[clicks_missing.columns[0],
                                                               'clicks'
                                                              ]]
median_x=[]
median_y=[]
for a in group_consecutive( date_clicks.index.to_list() ):
    median_idx=( a[0]+a[-1] )/2
    #print(clicks_missing[clicks_missing.index==a[0]-1].values[0][[0,3]])
    year,last_co2= clicks_missing[clicks_missing.index==a[0]-1].values[0][[0,3]]
    year,next_co2= clicks_missing[clicks_missing.index==a[-1]+1].values[0][[0,3]]
    median_co2 = ( last_co2 + next_co2)/2
    #print(last_co2, next_co2)
    median_x.append(median_idx)
    median_y.append(median_co2)
    
print(median_x)
print(median_y)

cols = ['date','clicks', 'linear', 'nearest', 'polynomial', 'spline']
plot_dfs( clicks_original, clicks_missing[cols], 'clicks', xlabel='date' )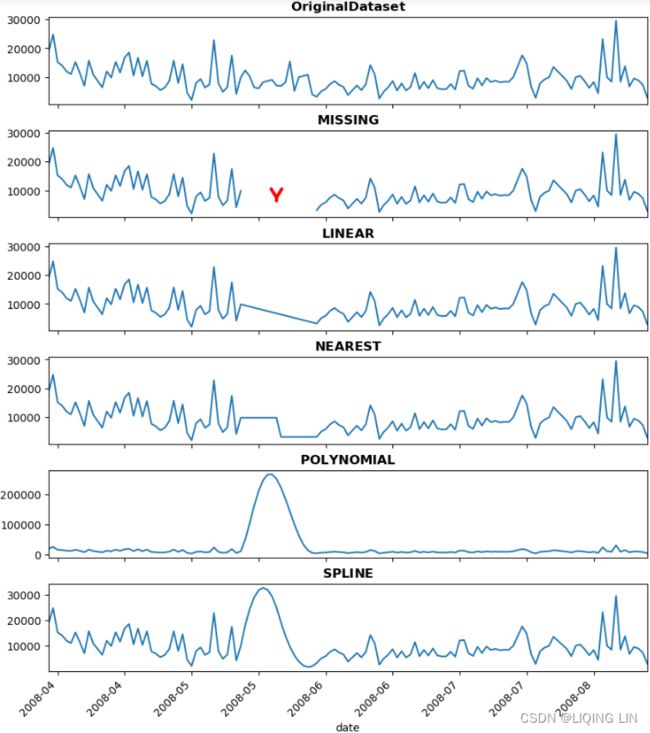

Figure 7.16 – Comparing the different interpolation strategies on the Clickstream dataset

Compare the results in Figure 7.16 with the original data in Figure 7.8.

From the output, you can see how the polynomial method exaggerated the curve when using 5 as the polynomial order. On the other hand, the Linear method attempts to draw a straight line.

One thing to note is that between the strategies implemented, only linear interpolation ignores the index, while the rest use numerical values for the index.

Overall, the interpolation technique detects patterns in neighboring data points (to the missing points) to predict what the missing values should be. The simplest form is linear interpolation, which assumes a straight line between two neighboring data points. On the other hand, a polynomial defines a curve between the two adjacent data points. Each interpolation method uses a different function and mechanism to predict the missing data.

In pandas, you will use the DataFrame.interpolate function. The default interpolation method is the linear interpolation ( method = "linear" ). There are additional parameters to provide more control over how the imputation with interpolation is done.

The limit parameter allows you to set the maximum number of consecutive NaN to fill. Recall in the previous recipe, Handling missing data with univariate imputation using pandas, that the Clickstream dataset had 16 consecutive missing points. You can limit the number of consecutive NaN , for example, to 5:

clicks_missing['clicks'].isna().sum()

example = clicks_missing['clicks'].interpolate(limit = 5)
example.isna().sum()

Only 5 data points were imputed; the remaining 11 were not.

Other libraries also ofer interpolation, including the following:

• SciPy provides a more extensive selection covering univariate and multivariate techniques: Interpolation (scipy.interpolate) — SciPy v1.9.3 Manual.
• NumPy offers a couple of interpolation options; the most widely used is the numpy.interp() function: numpy.interp — NumPy v1.24 Manual.

To learn more about DataFrame.interpolate , please visit the official documentation page here: pandas.DataFrame.interpolate — pandas 1.5.2 documentation.

ts7_Missing_imputation_interpolation_MICE_NaN NaT fillNA_IterativeImputer_FeatureUnion_iloc_识别列表连续组

Understanding missing data

RMSE for Evaluating Multiple Imputation Methods

Performing data quality checks

pandas automatically convert the empty values to np.NaN (missing)

auto convert the string placeholder(NaN, NaT, NA) values to np.NaN (missing)

Convert the 0 and ? values to NaN types

Covert the dtype(such as object) to the expected dtype(such as object)

Handling missing data with univariate imputation插补 using pandas

Handling missing data with univariate imputation using scikit-learn

Handling missing data with multivariate imputation

Bagging and Pasting

Extra-Trees

Elastic Net

6.4. Imputation of missing values

6.4.1. Univariate vs. Multivariate Imputation

6.4.2. Univariate feature imputation

6.4.3. Multivariate feature imputation

6.4.3.1. Flexibility of IterativeImputer

6.4.3.2. Multiple vs. Single Imputation

6.4.4. Nearest neighbors imputation

6.4.5. Keeping the number of features constants

6.4.6. Marking imputed values

6.4.7. Estimators that handle NaN values

MICE(Multivariate Imputation by Chained Equation)

Handling missing data with interpolation

你可能感兴趣的:(python,pandas,开发语言)