马尔科夫随机场：定义、性质，最大后验概率问题，能量最小化问题
文章目录
- 马尔可夫随机场
- 定义
-
- 前置知识：条件独立
- 马尔可夫的三个性质
- 马尔可夫三个性质的关系
- 团分解 Clique factorization
-
- 马尔可夫随机场联合概率密度可以进一步表示为以下分解模式
- 马尔可夫随机场的例子
- 成对马尔可夫随机场与其应用
马尔可夫随机场
马尔可夫随机场又称马尔可夫网络（Markov random field (MRF), Markov network or undirected graphical model）是具有马尔可夫属性的随机变量的集合，它由一个无向图来描述。
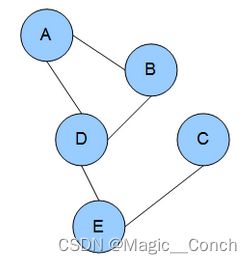上图就是马尔可夫随机场的例子，边代表依赖关系。上图中，A依赖于B、D，C依赖于E，以此类推。
定义
对给定无向图 G = ( V , E ) G=(V, E) G=(V,E)和一个由V索引的随机变量的集合 X = ( X v ) v ∈ V X=\left(X_{v}\right)_{v \in V} X=(Xv)v∈V，如果他们满足局部马尔可夫性质，就说X是关于G的马尔可夫随机场。
前置知识：条件独立
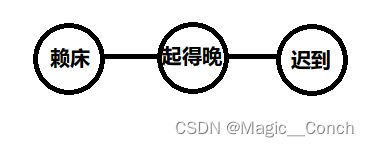
用上图的例子说明条件独立：赖床和起得晚互相有依赖，起得晚和迟到互相有依赖，但是如果提前知道起得晚的概率，赖床和起得晚就互相条件独立了。
马尔可夫的三个性质
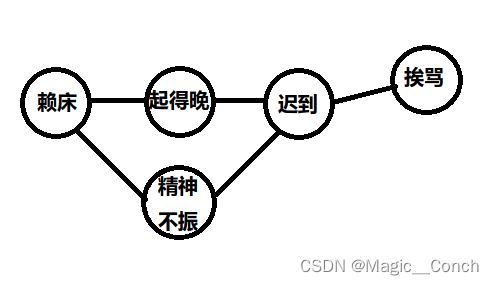
- 成对马尔可夫性质 Pairwise Markov property：给定所有其他变量，任何两个不相邻的变量是条件独立的。（比如知道了其他三个变量，赖床和迟到相互独立。）
X u ⊥ X v ∣ X V \ { u , v } X_{u} \perp X_{v} \mid X_{V \backslash\{u, v\}} Xu⊥Xv∣XV\{u,v} - 局部马尔可夫性质 Local Markov property：给定一个变量的所有邻接变量，该变量条件独立于所有其他变量（下式中， N ( v ) N(v) N(v)是v的邻接集合）。（比如知道了起得晚和精神不振变量，赖床和迟到、挨骂相互独立。）
X v ⊥ X V \ N [ v ] ∣ X N ( v ) X_{v} \perp X_{V \backslash \mathrm{N}[v]} \mid X_{\mathrm{N}(v)} Xv⊥XV\N[v]∣XN(v) - 全局马尔可夫性质：给定一个分离的子集，任何两个随机变量的子集都是条件独立的（下式中，任何由A集合的结点到B集合的结点的路径都要经过S内的结点）。（给定迟到，赖床、起得晚、精神不振这个集合内的变量和挨骂这个集合变量相互独立。）
X A ⊥ X B ∣ X S X_{A} \perp X_{B} \mid X_{S} XA⊥XB∣XS
上述公式中， ⊥ \perp ⊥代表相互独立， ∣ \mid ∣代表条件， \ \backslash \代表差集。
马尔可夫三个性质的关系
全局 > \gt >局部 > \gt >成对，然而上述的三个性质对于正分布来说是等价的（即非0概率分配）。
这三条性质的关系用下面的公式更好理解：
- Pairwise 成对：对任意不相等或不相邻的 i , j ∈ V i, j\in V i,j∈V，有 X i ⊥ X j ∣ X V \ { i , j } X_{i} \perp X_{j} \mid X_{V \backslash\{i, j\}} Xi⊥Xj∣XV\{i,j}。
- Local 局部：对任意 i ∈ V i \in V i∈V和 不包含或与 i i i邻接的集合 J ⊂ V J \subset V J⊂V，有 X i ⊥ X J ∣ X V \ ( { i } ∪ J ) X_{i} \perp X_{J} \mid X_{V \backslash(\{i\} \cup J)} Xi⊥XJ∣XV\({i}∪J)
- Global 全局：对任意不相交不邻接的 I , J ⊂ V I, J \subset V I,J⊂V，有 X I ⊥ X J ∣ X V \ ( I ∪ J ) X_{I} \perp X_{J} \mid X_{V \backslash(I \cup J)} XI⊥XJ∣XV\(I∪J)。
团分解 Clique factorization
直接根据马尔可夫随机场的性质来建立满足条件的概率分布是困难的，所以人们更普遍使用的一类马尔可夫随机场是能根据图的团进行分解的。
Clique 团：团是无向图顶点的子集，在这个子集中，每两个顶点都是邻接的。
更普遍使用的马尔可夫随机场公式如下：
P ( X = x ) = ∏ C ∈ cl ( G ) ϕ C ( x C ) P(X=x)=\prod_{C \in \operatorname{cl}(G)} \phi_{C}\left(x_{C}\right) P(X=x)=C∈cl(G)∏ϕC(xC)
上式中，X是联合概率密度；x不是单个值，而是一组值； c l ( G ) cl(G) cl(G)是G的团的集合；函数 ϕ C \phi_C ϕC是势函数，它可以指团（顶点）的势，也可以指因子（边）的势，根据实际建模需要而定。
马尔可夫随机场联合概率密度可以进一步表示为以下分解模式
P ( x 1 , … , x n ) = 1 Z Φ ∏ i = 1 ϕ i ( D i ) P\left(x_{1}, \ldots, x_{n}\right)=\frac{1}{Z_{\Phi}} \prod_{i=1} \phi_{i}\left(D_{i}\right) P(x1,…,xn)=ZΦ1i=1∏ϕi(Di)
其中， Z Φ Z_{\Phi} ZΦ为联合概率分布的归一化因子，通常称为配分函数(partition function)。 D i D_i Di是随机变量的集合，因子 ϕ i ( D i ) \phi_{i}\left(D_{i}\right) ϕi(Di)是从随机变量集合到实数域的一个映射，称为势函数或因子
Φ = { ϕ i ( D i ) , … , ϕ K ( D K ) } p ~ ( x 1 , … , x n ) = ∏ i = 1 ϕ i ( D i ) Z Φ = ∑ x 1 , … , x n p ~ ( x 1 , … , x n ) \begin{aligned} &\Phi=\left\{\phi_{i}\left(D_{i}\right), \ldots, \phi_{K}\left(D_{K}\right)\right\} \\ &\tilde{p}\left(x_{1}, \ldots, x_{n}\right)=\prod_{i=1} \phi_{i}\left(D_{i}\right) \\ &Z_{\Phi}=\sum_{x_{1}, \ldots, x_{n}} \tilde{p}\left(x_{1}, \ldots, x_{n}\right) \end{aligned} Φ={ϕi(Di),…,ϕK(DK)}p~(x1,…,xn)=i=1∏ϕi(Di)ZΦ=x1,…,xn∑p~(x1,…,xn)
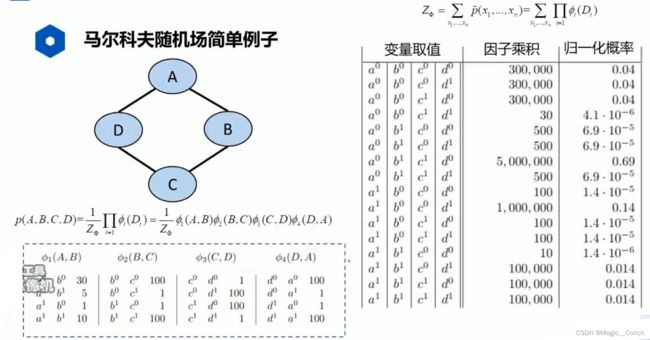
马尔可夫随机场的例子
局部势函数与边缘概率密度没有直接关系。
成对马尔可夫随机场与其应用
成对马尔可夫随机场的式子如下：
1 Z Φ ∏ p ∈ V ϕ p ( x p ) ∏ ( p , q ) ∈ E ϕ p q ( x p , x q ) \frac{1}{Z_{\Phi}} \prod_{p \in V} \phi_{p}\left(x_{p}\right) \prod_{(p, q) \in E} \phi_{p q}\left(x_{p}, x_{q}\right) ZΦ1p∈V∏ϕp(xp)(p,q)∈E∏ϕpq(xp,xq)
图像处理问题往往可以转化为定义在MRF上的最大后验概率问题：
max x p ( x ) ∝ ∏ p ∈ V ϕ p ( x p ) ∏ ( p , q ) ∈ E ϕ p q ( x p , x q ) \max _{\mathbf{x}} p(\mathbf{x}) \propto \prod_{p \in V} \phi_{p}\left(x_{p}\right) \prod_{(p, q) \in E} \phi_{p q}\left(x_{p}, x_{q}\right) xmaxp(x)∝p∈V∏ϕp(xp)(p,q)∈E∏ϕpq(xp,xq)
即求 p ( x ) p(x) p(x)最小时，x的取值，如下图所示。
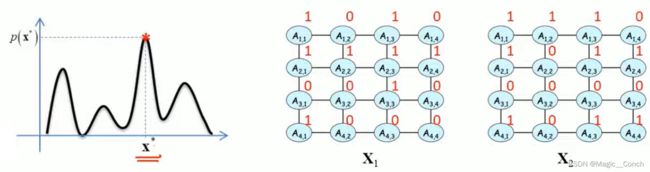
最大后验推理问题等价于能量最小化问题，令 θ p ( x p ) = − log ϕ p ( x p ) , θ p q ( x p , x q ) = − log ϕ p q ( x p , x q ) \theta_{p}\left(x_{p}\right)=-\log \phi_{p}\left(x_{p}\right), \theta_{p q}\left(x_{p}, x_{q}\right)=-\log \phi_{p q}\left(x_{p}, x_{q}\right) θp(xp)=−logϕp(xp),θpq(xp,xq)=−logϕpq(xp,xq)，有：
min x E ( x ) = ∑ p ∈ V θ p ( x p ) + ∑ ( p , q ) ∈ E θ p q ( x p , x q ) \min _{x} E(\mathbf{x})=\sum_{p \in V} \theta_{p}\left(x_{p}\right)+\sum_{(p, q) \in E} \theta_{p q}\left(x_{p}, x_{q}\right) xminE(x)=p∈V∑θp(xp)+(p,q)∈E∑θpq(xp,xq)
势函数的假设：连续像素点的取值具有连续性。