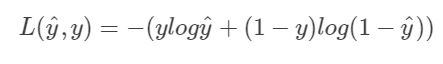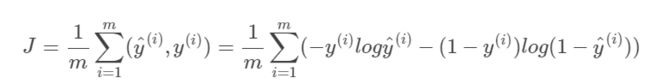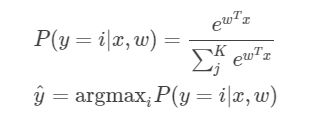SVM + 决策树 + 提升方法 (还有LR、最大熵、)
ROC曲线 和 AUC曲线
ROC (Recieve Operating Characteristic Curve), 接受者操作特征曲线。
横坐标 FPR(假阳率) 纵坐标TPR(真阳率), 绘制在图中,改变阈值,又是一条新曲线。
曲线越靠近左上角,效果越好。。。
AUC(Area Under the Curve of ROC), ROC曲线下面的面积。。、
绘制ROC曲线, ROC曲线下面的面积就是AUC的值。。 计算ACC准确率。。
特征选择
特征选择要考虑的点:
- 特征是否发散, 方差几乎为0的,也就是说样本在这个特征上没有差异, 就不行。
- 特征与目标的相关性,相关性越高的,优先选择。
特征选择的两个目的:
3. 减少特征的数量,达到降维的目的,防止过拟合,提高模型的性能;
4. 增加对特征值的理解。
特征选择的方法有三类:
1.Filter(过滤法) 移除方差过低的,
单变量的特征选择
卡方检验,
-
Wrapper(包装法):根据目标函数(通常是预测效果),每次选择若干特征,或者排除若干特征。
-
Embedded(嵌入法):先使用某些机器学习算法和模型进行训练,得到各个特征的权重系数,判断特征优劣,然后再进行过滤。
有些机器学习模型本身就具有对特征进行打分的机制,因此,很容易用到特征选择中。
回归模型: 等价于回归问题中的评估 皮尔森相关系数。
Online Learning
https://blog.csdn.net/hzwaxx/article/details/83867630
Online Learning并不是一种模型,而是一种模型的训练方法。 根据线上反馈数据,实时快速的进行模型调整,使得模型及时反映线上的变化,提高线上预测的准确率。
流程: 将模型的预测结果展现给用户,然后收集用户的反馈数据,再来训练模型,形成闭环系统。
美团等平台使用,推荐 重排序。
传统的训练方法,上线后,更新周期过长, 模型上线后是静态的。 不会和线上的状况进行互动。
Online Learning:根据线上预测结果及时作出修正。及时反应线上变化。
- Bayesian Online Learning
给出先验概率, 根据反馈结果计算后验, 将其作为下一次的先验概率,如此迭代下去。,
SVM
LibSVM 和 LibLinear
(1)LibSVM:
非线性SVM分类器, 通用的SVM分类器,
在样本有限的情况下, 核映射可能不准确, 性能不一定有线性的好。 造成比线性 更差的结果。
(2)LibLinear:
用于大规模的数据, 训练线性分类器。 针对大规模数据,线性分类器模型简单很多,性能也还不错。 主要训练速度很快,不用核处理,
占内存。 处理速度快,对于稀疏特征。
数据量足够多, 特征维度足够大,可以用线性模型。
特征数,小于样本数, 最好使用RBF, 非要用线性的化,也用liblinear。
SVM(Support Vector Machines),支持向量机, 是一种二分类模型, 基本模型是定义在特征空间上的间隔最大的线性分类器,
核函数的使用,使它成为实质上的非线性分类器,
学习策略,间隔最大化,
三类支持向量机:
1)线性可分的支持向量机,(通过硬间隔最大化,学习线性分类器,即线性可分支持向量机,又称硬间隔支持向量机)
支持向量:线性可分情况下,样本点中与分离超平面距离最近的样本点的实例,称为支持向量。
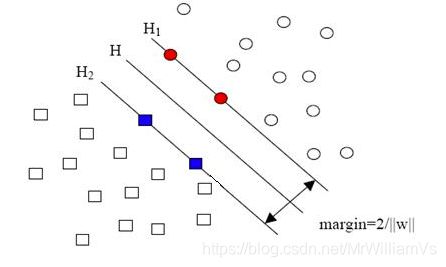
求解线性可分支持向量机的最优化问题,作为原始最优化问题,应用拉格朗日对偶性,求解对偶问题得到原始问题的最优解。 这就是线性可分支持向量机的最优解。
对偶问题更容易求解; 自然引入核函数,推广到非线性分类问题。
原始的极大极小的问题,转化为了求极小的约束问题。
先求对偶问题的解alpha, 再求原始问题的解w、b。 从而得到分离超平面和分类决策函数。
2)线性支持向量机,
(数据近似线性可分时,(含有极个别噪声),函数间隔加上一个松弛变量
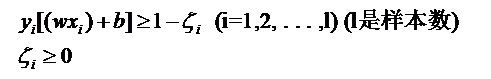
目标函数也加上松弛变量和惩罚函数C
通过软间隔最大化,学习一个线性的分类器,线性支持向量机,又称软间隔支持向量机)
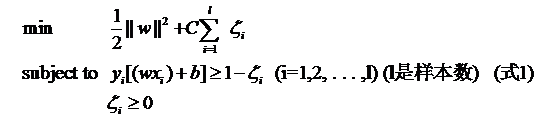
对偶方法去求解。
3)非线性支持向量机。(数据线性不可分时,使用核技巧和软间隔最大化,学习非线性支持向量机)(简单模型是复杂的基础)
核函数(Kernel Function): 表示将输入,从输入空间映射到特征空间得到的特征向量之间的内积。
隐式的在高维特征空间中学习线性支持向量机,比支持向量机更一般的机器学习方法。
求解方法: SMO算法
输入空间核特征空间是两个不同的空间。
输入空间:为欧式空间或离散集合,
特征空间:欧式空间或希尔伯特空间。
线性可分支持向量机,线性支持向量机,假设这两个空间的元素,一一对应。 将输入空间中的输入映射到特征空间中的特征向量。
输入都是由输入空间转换到特征空间,支持向量机的学习是在特征空间进行的。
感知机:利用误差最小策略,会存在无数个分离超平面。(
线性可分支持向量机:利用间隔最大化,求最优分离超平面。解是唯一的,
函数间隔(functional margin): y (wx + b), 表示分类是否正确及确信程度。
几何间隔: 对分离超平面的法向量w加某些约束,如规范化,使得间隔是确定的。
支持向量机: 求解能够正确划分训练数据集,并且几何间隔最大的分离超平面。
就是说,以充分大的确信度对训练数据进行分类。 也就是说,对预测数据也会有很好的分类预测能力。
SMO:(最小最优化算法,Sequential Minimal Optimization),实现快速高效的支持向量机学习。满足KKT条件。
决策树:
1)所有数据多可以看成是一个节点。2)根据分裂准则,从所有属性中挑选一个对节点进行分割,
递归返回的三种情况:1)当前节点包含的样本全属于同一类别,无需划分;2)当前属性集为空,或所有样本在所有属性上取值相同,无法划分;3)当前节点包含的样本集为空,不能划分。
划分准则:分支节点包含的样本尽可能属于同一类别, 节点的纯度越来越高。
信息熵:
对于样本集合D来说,pk是第k类样本所占比例。
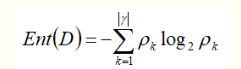
当某一类比例为1时,信息熵最小(纯度最高),为0.
当所有类别比例相同时,信息熵最大(纯度最低),![]()
gama是类别数量。
信息增益
根据信息熵, 属性a有V个不同取值, 第v个分支节点上的样本为Dv,可计算分支节点上的信息熵,
根据每个节点上的样本占比,给分支节点赋予权重 |Dv| / |D|,
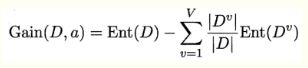
信息增益越大,用属性a进行划分所获得的“纯度提升”越大。
评价:对可取值数目较多的属性有所偏好,比如每一类别对应一个样本,这样信息增益最大,并且不具备泛化能力。 ID3算法。
增益率
C4.5 算法。

IV(a) 称为a的固有值, a的可能取值数目越多,IV(a)的值越大。
从候选属性中选择信息增益高于平均水平的属性, 再从中选择增益率最高的。
基尼指数
CART决策树,使用 基尼指数 来进行划分属性。

Gini值越小,D的纯度越高。(从数据集D中随机抽取2个样本,类别标记不一样的概率)
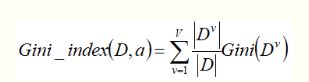
上面是,属性a的基尼指数, 选择上式最小的属性a,作为划分属性。
https://www.cnblogs.com/liuqing910/p/9121736.html
剪枝, 防止过拟合。
首先定义损失函数,正则化的极大似然函数。 选取最优特征,去分割训练数据,然后对子集继续分类, 直到没有合适的特征为止。。
这种方式,容易过拟合, 需要剪枝。 树变得简单,去掉过于细分的节点,
1。 特征选择, 信息增益,或者(信息增益比, Information Gain)
2. 决策树的生成, 对应模型的局部选择。 只考虑局部最优。 常用的, ID3, C4.5, CART。
1)ID3:用信息增益,每次选取信息增益最大的点,递归生成。用极大似然法进行模型选择。
2)C4.5,优化:用信息增益比,
3)CART: 分类与回归树,也是由特征选择,树的生成,树的剪枝组成,既可以用于分类,也可以用于回归。
树的生成:尽可能大;
树的剪枝:用验证数据集,对已生成的树剪枝,并选取最优树。
分类树:基尼指数(Gini index),特征选择。
回归树:平方误差最小化。
3.决策树的剪枝。对应模型的全局优化。极小化决策树的损失函数,平衡模型复杂度和模型拟合的损失函数。
提升(Boosting): 常用的统计学习方法, 改变训练样本的权重,学习多个分类器,并将这些分类器进行线性组合,提高分类性能。
提升方法的具体思路:对于复杂的任务,将多个专家的判断进行适当综合,得出的判断比其中任何一个专家要好。
AdaBoost,代表性的提升算法。
Boosting Tree, 提升树,提升方法的一个具体实例。
强可学习(strongly learnable): 存在一个多项式的学习算法,能够学习它,正确率很高。
弱可学习(weakly learnable):学习的正确率仅比随机猜测的略好,就是弱可学习。
发现弱学习算法容易的多, 可以将弱学习算法提升为强学习算法。
提升方法(Boosting): 1. 改变训练数据的概率分布,学习一系列弱分类器,2. 组合,构成一个强分类器。
- 提高错误分类的样本的权值,降低分类正确样本的权值,
- 加大分类误差小的弱分类器的权值, 在投票表决中起较大的作用。
Bagging(套袋法):
http://www.cnblogs.com/earendil/p/8872001.html
Bagging 和 Boosting:
样本选择上,
Boosting; 每一轮的训练集不变,只是训练集中每个样例在分类器中的权重发生变化, 各个预测函数只能顺序生成,后一个模型需要前一个模型的结果去进行调整。
Bagging:训练集是在原始数据集中有放回的选取,选出的各轮训练集之间独立。(交叉验证是一个应用例子) 对选取的k个训练集, 得到k个模型。 k个模型采用投票的方式得到结果; 或者均值作为最终结果。 每个预测函数可以并行生成。
Bagging: 减小了variance(方差), 训练的各个模型有近似相等的bias和variance。
bias(偏离, 偏置) 和 variance(方差) 之间的 权衡。
https://www.cnblogs.com/ooon/p/5711516.html
一个预测模型的误差 Error = Bias*Bias + Variance + Noise
Bias: 模型的 期望输出与真实输出的偏离程度,表示模型的拟合能力,偏高的话说明预测结果与真实结果差异很大;
Variance: 同样大小的不同的数据集训练出的模型与他们期望输出值的差异, 训练集变化,则性能变化, 偏高则说明模型很不稳定。
Noise: 表明了当前任务,任何算法所能达到的误差下界,表明问题本身的难度。
最大熵
最大熵 是 概率模型学习的一个准则, 将其推广到分类问题,得到最大熵模型。(ME, Maximum Entropy)
LR(Logistic Regression),统计学习中的经典分类算法。
最大熵和逻辑斯蒂 都是 对数线性模型。
逻辑斯蒂: 分布函数F(X): 是一条Sigmoid形曲线, 密度函数f(x),
二项逻辑斯蒂回归(binomial):用于二分类。
多项逻辑斯蒂回归(multi-nominal):用于多分类。
最大熵原理:学习概率模型时,在所有可能的概率模型(分布)中,熵最大的模型是最好的模型。
均匀分布时,熵最大。
最大熵原理,用到分类任务中,得到最大熵模型。
最大熵模型的学习过程,就是求解最大熵模型的过程。形式化为约束最优化问题。
LR:
梯度下降法,求解LR的参数

模型优化,防止过拟合,控制复杂度,引入正则化
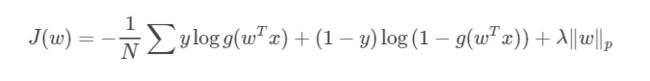
SVM和LR的对比
SVM和LR
SVM
https://blog.csdn.net/b285795298/article/details/81977271
从机器学习三要素总结, 决策函数, 损失函数, 学习算法。
以及算法复杂度, 鲁棒性。
损失函数: LR是交叉熵损失, SVM是hinge loss
学习算法: LR是梯度下降, SVM是SMO
算法鲁棒性: SVM只依赖于支持向量(对异常数据不敏感,鲁棒性高点),LR依赖所有数据
算法复杂度:SVM具有很强的非线性学习能力, LR只能学到线性关系。
LR可以很方便的扩展到多类别分类,
SVM需要使用多个二分类这种思路。
线性可分问题: 硬间隔最大化。
SVM
学习策略:在特征空间上间隔最大化, 可转化为求解凸二次规划的最优化问题,或者正则化的合页损失函数最小化问题。
由简到繁,三类情况。 简单模型是复杂模型的基础,也是复杂模型的特殊情况。
1)线性可分,支持向量机
训练数据线性可分时,通过硬间隔最大化,学习一个线性分类器, 就是线性可分支持向量机,又称硬间隔支持向量机。
间隔最大,求得的解是唯一的。
函数间隔:
几何间隔:函数间隔加上约束规范化,间隔就是确定的。这时函数间隔叫做几何间隔。
2)线性支持向量机
训练数据近似线性可分,通过软间隔最大化,学习一个线性分类器,即线性支持向量机,又称软间隔支持向量机。
某些样本点,不满足函数间隔>=1的约束条件,对每个样本点加入
松弛变量
目标函数 再加上一个关于松弛变量的惩罚项*C。
损失函数是 合页损失函数(hinge loss function)
3)非线性支持向量机
训练数据线性不可分,通过核技巧,软间隔最大化,学习非线性支持向量机。
核函数将输入从输入空间映射到特征空间得到的特征向量之间的内积,等价于在高维特征空间中,学习线性支持向量机。