实验一:人工智能之启发式搜索算法(含源码+实验报告)
文章目录
- 第1关:A*搜索求解8数码问题
-
- 任务描述
- 相关知识
-
- 评估函数
- 贪婪最佳优先搜索
- A*搜索:缩小总评估代价
- 求解思路
- 编程要求
- 测试说明
- 解题思路
- 算法伪代码
- 实验结果分析
- 总结
- 实验源码
第1关:A*搜索求解8数码问题
任务描述
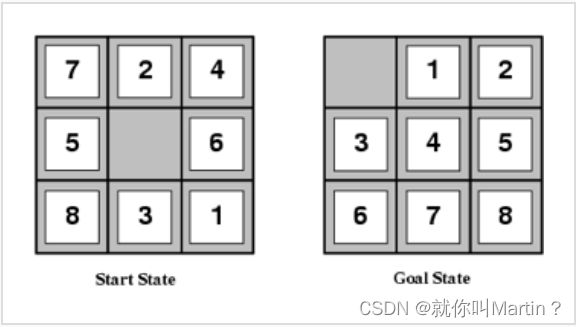
本关任务:八数码问题是在一个3×3的棋盘上有1−8位数字随机分布,以及一个空格,与空格相连的棋子可以滑动到空格中,问题的解是通过空格滑动,使得棋盘转化为目标状态,如下图所示。
为了简化问题的输入,首先将空格用数字0表示,然后将3×3的棋盘用9位长的字符串表示,则上图的初始状态为724506831,目标状态为012345678,本关卡所有目标状态均为012345678,也保证初始状态到目标状态有解。
对于上图的初始状态,将数字2移动到空格,称之为u操作(空格上移),将数字3移动到空格,称之为d操作(空格下移),将数字5移动到空格,称之为l操作(空格左移),将数字6移动到空格,称之为r操作(空格右移),则一个合法移动路径为lurdrdllurrdllurrulldrrull。
724 724 024 204 254 ... 012
506 056 756 756 706 ... 345
831 831 831 831 831 ... 678
l u r d ... l
相关知识
为了完成本关任务,你需要掌握:1.评估函数,2.贪婪最佳优先搜索,3.A*搜索:缩小总评估代价,4.求解思路。
评估函数
在有信息搜索 Informed Search 策略中,常使用的是最佳优先搜索 Best First Search
,它的结点扩展是基于评估函数值f(n)选择的。评估函数被看做是代价估计,因此代价最低的结点最先被选择扩展。对f(n)的选择决定了搜索策略,大部分的最佳优先搜索算法的f(n)由启发式函数h(n)构成:
h(n)=结点n到目标的最小代价路径的代价估计值
贪婪最佳优先搜索
贪婪最佳优先搜索 Greedy Best-First Search
试图扩展距离目标结点最近的结点,原因是这种策略可能可以非常快的找到解,因此,贪婪最佳优先搜索只使用启发式信息,即f(n)=h(n)。
A*搜索:缩小总评估代价
A* 搜索(A 星搜索)是最广为人知的最佳优先搜索,它对结点n的代价评估结合了g(n),即到达此结点n已经花费的路径代价,和h(n),即从该结点n到目标结点所花代价。
f(n)=g(n)+h(n)
由于g(n)是从开始结点到结点n的路径代价,而h(n)是从结点n到目标结点的最小路径代价的估计值因此:
f(n)=经过结点n的最小代价解的估计代价
所以,要寻找最小代价的解,首先扩展的是g(n)+h(n)值最小的结点。可以发现,A* 搜索算法与一致代价搜索算法类似,区别是 A* 搜索算法使用g(n)+h(n)而不是g(n)。
求解思路
该问题是将与空格相连的数字移动到空格的位置上,也就相当于将空格移动到与之相连的位置,因此,以空格为当前结点,扩展结点可能为上下左右四个相连的位置,若使用一般的搜索算法,可能陷入无限搜索中,永远搜不到目标解,而 A* 搜索算法则能非常好的将搜索过程导向求解目标。
问题给的是字符串数据724506831,可以还原成如下形式:
对应8数码状态 8数码状态下标ID
字符串:724506831 7 2 4 0 1 2
下标ID:012345678 5 0 6 3 4 5
8 3 1 6 7 8
那么空格的l移动操作即为下标4和下标3上所对应的数字的交换,分别为0和5,交换后的新的状态为:
对应8数码状态 8数码状态下标ID
字符串:724056831 7 2 4 0 1 2
下标ID:012345678 0 5 6 3 4 5
8 3 1 6 7 8
以此类推,空格的lrud各操作均可用以上的交换过程表达。
A* 算法的重中之重就是启发式函数h(n)的设计,不同的设计方法可能产生不同的求解路径。在这里,可以选择欧氏距离作为评估函数值:除0之外,各个数字在当前状态的下标与目标状态的下标的绝对值之和。例如:当前状态为123456780,目标状态为:012345678,数字1的下标分别为0和1,数字2的下标分别为1和2,…,数字8的下标分别为7和8,则当前状态与目标状态的评估值为h(n)=abs(1−2)+abs(2−3)+⋯+abs(7−8)=8。
编程要求
本关的编程任务是补全右侧代码片段 salvePuzzle 、 calcDistH 和 moveMap 中 Begin 至 End 中间的代码,具体要求如下:
在 salvePuzzle 中,根据输入参数init(初始状态,如724506831)和targ(目标状态,均为012345678),实现 A* 搜索算法,返回八数码问题的移动路径,如上图的移动路径:lurdrdllurrdllurrulldrrull。
在 calcDistH 中,计算当前状态(参数srcmap,如724506831)到目标状态(参数destmap,如012345678)的启发式函数值h(n),并返回h(n)。
在 moveMap 中,实现行动转换,并返回下一个状态,例如当前状态为参数curmap=724506831,当前 8 数码状态curmap中空格 0 的位置索引i=4,移动空格到位置j=3,则返回的新状态为newmap=724056831。
测试说明
平台将自动编译补全后的代码,并生成若干组测试数据,接着测试程序会调用上述函数,并判断函数返回的路径是否为合法解,若是则输出 Accepted 表示程序正确,否则程序错误。
以下是平台的测试样例:
测试输入:
724506831
预期输出:
Accepted
开始你的任务吧,祝你成功!
解题思路
1、整体思路
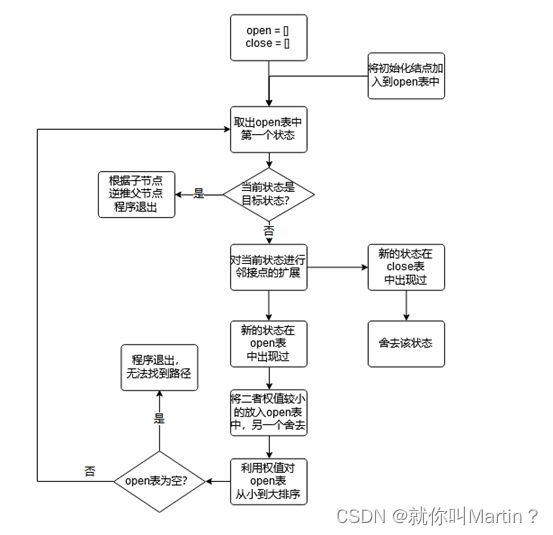
首先建立一个open表,一个close表,分别用于待存放的状态和已经使用过的状态。每次从open表中取出一个权值最小的状态,对其进行邻接点的扩展,若新的点在close表中,则舍去,若在open表中,则比较二者的权值,取最小的权值作为新的点。若都不存在,则把此状态添加到open表中,直到当前状态为目标状态,程序结束。根据最终状态逆推回去父节点,则找到了路径。
算法伪代码
1、状态转换,moveMap(cur_map,i,j)
1)程序输入:
Cur_map:当前状态;
i,j: 互换的位置;
2)程序返回:
转换后的状态;
3)程序思路:
-
if i>j: -
i,j=j,i -
tmp_i = cur_map[i] //存放i对应的值 -
tmp_j = cur_map[j] //存放j对应的值 -
tmp_map = cur_map[:i]+tmp_j+cur_map[i+1:j]+tmp_i+cur_map[j+1:] -
return tmp_map
2、启发式函数h(n),calcDistH(src_map,dest,map)
1)程序输入:
Src_map:源状态
Dest_map: 目标状态
2)程序返回:
源状态和目标状态的欧式距离。
3)程序思路:
因为字符串长度为9,所以需要遍历字符串需要9次,每次遍历时,对连个字符串的相同位置进行绝对值差值运算,最后累加。
-
clf = 0//累加欧式距离 -
for i in range(9): -
clf += abs(int(src_map[i])-int(dest_map[i])) -
return clf
4、主程序,salvePuzzle(init,targ)
1)程序输入:
init:输入状态
targ: 最终状态
2)程序返回:
有”urld”组成的路径。
3)程序思路:
1>第一部分,构建open表和close表,寻找路径。
1. Open = [init]//构建初始open表
2. Close = []//构建初始close表
3. While True:
4. Current = Open.pop(0) //权值最小的
5. Close.append(current)
6. If Current == targ://跳出条件
7. Break
8. Else:
9. New_state = Find_near(current)//对邻接点扩充
10. If new_state in close: //如果在close表,则舍去
11. Break
12. if new_state in open: //如果在open表,则判断
13. if new_state.val < old_state.val: //新的结点权值更小,替换
14. exchange(old_state,new_state)
15. if new_state not in open:
16. open.append(new_state)
17. open.sort()//根据权值排序
2>对邻接点扩充:
1. Current = Open[0]
2. Id = current.find(‘0’) //找到空格“0”的索引
3. if str(Id) not in '036': //可以左移
4. new_state = moveMap(current,Id,Id-1)
5. if str(Id) not in '258': //可以右移
6. new_state = moveMap(current,Id,Id+1)
7. if Id-3>=0: //可以上移
8. new_state = moveMap(current,Id,Id-3)
9. if Id+3<=8: //可以下移
10. new_state = moveMap(current,Id,Id+3)
3>结点权值f(n)的计算:
1. h(n) = calcDishH(current,targ)
2. f(n) = current.father.val + 2
3. Current.val = h(n) + f(n)
4>根据子节点逆推父节点:
1. Current = targ
2. Clf = ‘’//待返回的操作顺序
3. While Current != init: //跳出条件
4. For item in close:
5. If current.Father == item: //找到父节点
6. Clf += item.flag //flag为lurd
7. Current = item
8. Return Clf[::-1] //因为是逆推,所以需要翻转字符串
实验结果分析
通过实验结果可得,我已完成实验要求,正确得到预计的实验结果。
在本次实验中,起初,我将g(n)设置为初始值+1,经过运算发现结果不太相符合,仔细琢磨。可能的原因是h(n)用欧氏距离和g(n)相比可能太大了,g(n)产生的作用会变小,所以改为g(n)+2。
在对比实验中,起初放弃考虑了g(n)的值,将此实验作为了爬山实验,经过与结果对比,发现它也能得到解,但不是最优解,应该与它未考虑步长有关系,此次对比实验证明,A搜索算法在最终结果上优于爬山搜素。经过与单纯的BFS对比,发现A启发式搜索比BFS快了近10倍,由此可见可见启发式搜索的优势(测试平台是VSCode,python3)
本次实验还有需要改进的地方:
在边界检查上用了大量的if-else语句,将4中情况分开讨论,降低了代码运行速率。
总结
首先建立一个open表,一个close表,分别用于待存放的状态和已经使用过的状态。每次从open表中取出一个权值最小的状态,对其进行邻接点的扩展,在扩展时要考虑是否超出边界。扩展时的权值为f(n)=h(n)+g(n),h(n)在本题中是欧式距离,g(n)在本题中是步长,走过的步数。若新的点在close表中,则舍去,若在open表中,则比较二者的权值,取最小的权值作为新的点。若都不存在,则把此状态添加到open表中,直到当前状态为目标状态。程序结束。根据最终状态逆推回去父节点(此步骤的完成,需要依靠close表,close表中的数据格式包括当前结点,父节点,g(n)的值,h(n)的值和对应的‘urld’操作),则找到了路径的反向,此时需要逆转则得到了正确的路径。
实验源码
# -*- coding:utf-8 -*-
class Solution:
def salvePuzzle(self, init, targ):
''' 求解8数码问题
参数:
init - 初始状态 例如'123046758'
targ - 目标状态 均为'012345678'
返回值:
clf - 由udlr组成的移动路径字符串
'''
#请在这里补充代码,完成本关任务
#********** Begin **********#
clf = ''
# 状态表
state_open = []
state_close = []
state_open.append([init,99,'test',init,0])
# fn 步深
fn = 2
flag = 1
while True:
#print('state_open',state_open)
#print('state_close',state_close)
cur_state = state_open.pop(0)
state_close.append(cur_state)
if cur_state[0] == targ :
# break
# print(cur_state)
# print('state_close',state_close)
# lurdrdllurrdllurrulldrrull
while 1:
#print(cur_state)
clf += cur_state[2]
if cur_state[3] == init:
break
for id,item in enumerate(state_close[1:]):
if item[0] == cur_state[3]: #找到父节点
cur_state = item
#print(len(clf))
return clf[::-1]
i = cur_state[0].find('0')
# print(cur_state)
flag = 1
# 空格左移 l
if str(i) not in '036':
tmp_map = self.moveMap(cur_state[0],i,i-1)
if tmp_map not in [tmp[0] for tmp in state_close]:
for id,item in enumerate(state_open):
# 存在一样的状态
# print('检查')
if item[0] == tmp_map:
# 新状态更优,替换
if item[1] + item[4] > self.calcDistH(tmp_map,targ) + cur_state[4] + fn:
state_open[id] = [tmp_map,self.calcDistH(tmp_map,targ),'l',cur_state[0],cur_state[4]+fn]
# print('ti')
flag = 0
break
break
# 不存在一样的状态
if flag == 1:
state_open.append([tmp_map,self.calcDistH(tmp_map,targ),'l',cur_state[0],cur_state[4]+fn])
flag = 1
# 空格右移 r
if str(i) not in '258':
tmp_map = self.moveMap(cur_state[0],i,i+1)
if tmp_map not in [tmp[0] for tmp in state_close]:
for id,item in enumerate(state_open):
if item[0] == tmp_map:
if item[1] + item[4] > self.calcDistH(tmp_map,targ) + cur_state[4] + fn:
state_open[id] = [tmp_map,self.calcDistH(tmp_map,targ),'r',cur_state[0],cur_state[4]+fn]
flag = 0
break
# 不存在一样的状态
if flag ==1:
state_open.append([tmp_map,self.calcDistH(tmp_map,targ),'r',cur_state[0],cur_state[4]+fn])
flag = 1
# 空格上移 u
if i-3>=0:
tmp_map = self.moveMap(cur_state[0],i,i-3)
if tmp_map not in [tmp[0] for tmp in state_close]:
for id,item in enumerate(state_open):
if item[0] == tmp_map:
if item[1] + item[4] > self.calcDistH(tmp_map,targ) + cur_state[4] + fn:
state_open[id] = [tmp_map,self.calcDistH(tmp_map,targ),'u',cur_state[0],cur_state[4]+fn]
flag = 0
break
# 不存在一样的状态
if flag ==1:
state_open.append([tmp_map,self.calcDistH(tmp_map,targ),'u',cur_state[0],cur_state[4]+fn])
flag = 1
# 空格下移 d
if i+3<=8:
tmp_map = self.moveMap(cur_state[0],i,i+3)
if tmp_map not in [tmp[0] for tmp in state_close]:
for id,item in enumerate(state_open):
if item[0] == tmp_map:
if item[1] + item[4] > self.calcDistH(tmp_map,targ) + cur_state[4] + fn:
state_open[id] = [tmp_map,self.calcDistH(tmp_map,targ),'d',cur_state[0],cur_state[4]+fn]
flag = 0
break
# 不存在一样的状态
if flag ==1:
state_open.append([tmp_map,self.calcDistH(tmp_map,targ),'d',cur_state[0],cur_state[4]+fn])
#print(tmp)
# 从小到大排序h(n) 启发搜索值
state_open.sort(key=lambda x : x[1] + x[4])
#state_open.sort(key=lambda x : x[1] )
# state_list += [tmp_state_list[0][:2]] #前两个
# clf += tmp_state_list[0][2] #状态
# next_map = tmp_state_list[0][0]
# init = next_map
# print('state_list',state_list)
# print(clf)
# index +=1
# print('init',init)
# exit(0)
#********** End **********#
def calcDistH(self, src_map, dest_map):
'''启发式函数h(n)
参数:
src_map - 当前8数码状态
dest_map - 目标8数码状态
返回值:
clf - 当前状态到目标状态的启发式函数值
'''
#请在这里补充代码,完成本关任务
#********** Begin **********#
clf = 0
for i in range(9):
clf += abs(int(src_map[i])-int(dest_map[i]))
#print(clf)
return clf
#********** End **********#
def moveMap(self, cur_map, i, j):
'''状态转换(交换位置i和j)
参数:
cur_map - 当前8数码状态
i - 当前8数码状态中空格0的位置索引
j - 将空格0的位置i移动到位置j,位置j移动到位置i
返回值:
clf - 新的8数码状态
'''
#请在这里补充代码,完成本关任务
#********** Begin **********#
# print(i,j)
if i>j:
i,j=j,i
tmp_i = cur_map[i]
tmp_j = cur_map[j]
tmp_map = cur_map[:i]+tmp_j+cur_map[i+1:j]+tmp_i+cur_map[j+1:]
return tmp_map
#********** End **********#