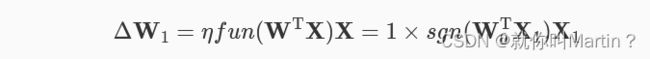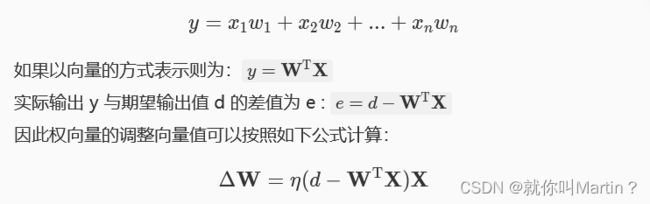实验三：神经网络之网络基础、第3关：常见学习方法

任务描述

本关任务：通过学习神经网络常见的学习方法，完成相应选择题。

相关知识

为了完成本关任务，你需要掌握：

1. 误差修正学习；
2. 赫布学习法则；
3. 最小均方规则。

误差修正学习

误差修正学习也叫 Delta 学习规则 。 误差修正学习通常与监督学习一起使用，是将系统输出与期望输出值进行比较，并使用该误差来改进模型参数 。最直接的方法是可以使用误差值来调整权值，使用诸如反向传播算法的方式 。
误差修正学习方法尝试在每次训练迭代时最小化该误差信号 。 采用误差修正学习的最流行的学习算法是反向传播算法。
神经元的作用是基于输入向量X=(x1​,x2​,x3​,…,xn​)产生相应的输出y。训练样本是一系列己知的 x和y^{​数据集，其中y}​表示预期的正确输出。我们可以使用如下公式描述实际输出和预期输出之间的误差：

E=21​(y−y^​)2

此处使用的误差函数也可以使用其他的误差函数代替。学习训练的过程是减少错误E， 直至趋近于 0 为最佳。 神经元的错误通过迭代得到最小值，每次根据当前情况进行一点修正 ， 逐渐找到最小目标函数，这与生物神经元逐渐生长的策略有一定相似度 。我们一般使用的找到最小值的方法是梯度下降，这个算法将在后面进行讲解。

赫布学习法则

赫布理论（ Hebbian Theory ）是一种神经科学理论，提出了在学习过程中对大脑神经元适应性的解释，描述了突触可塑性的基本机制， 其中突触功效的增加来源于突触前细胞重复和持续剌激突触后细胞 。
赫布学习规则是最简单、最传统的神经元学习规则 。 从人工神经元和神经网络的角度来看，赫布学习规则的原理可以被描述为一种确定如何改变模型神经元之间权值的方法 。
如果两个神经元同时被激活， 则这两个神经元之间的权值就会增加 ： 如果它们分别被激活，则它们之间的权值会降低。
赫布学习法则中倾向于同时为正或为负的节点具有较强的正权值，而倾向于相反的那些节点具有较强的负权值，这点与“条件反射 ”有一定的相似性 ， 赫布学习规则代表一种纯前馈、 无监督学习 。
一个简单的赫布学习公式：
wij​=xi​xj​，其中 wij​表示神经元 j 到神经元 i的连接权值， xi​表示神经元i的输入。值得说明的是， 一般而言，当 i 等于 j时， wij​ 的值恒为 0。而对于调节的Δwij​，则为Δwij​=wij​(n+1)−wij​(n)=ηyi​wj​，wij​(n+1)表示己经进行n+1次调整权值之后从节点j到节点 i的连接权值，η是学习速率， xj​为节点j的输出也作为节点i的输入， yi​为节点 i的输 出 。
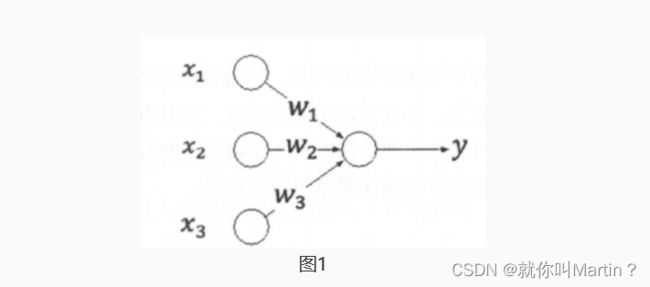
对于赫布学习规则，神经元的输出值可以用 fun(WTX)表示，因此ΔW=ηfun(WTX)X。我们通过一个例子来理解。如图1是一个简单的神经网络：

图中，输入向量X=[x1​,x2​,x3​]T，权值向量W=[w1​,w2​,w3​]T，设定初始权值向量的值为 W0​=[1,0.5,−1]T ，训练数据三组输入向量X1​=[1,0.5,1]T 、 X2​=[−2,1,2]T 、X3​=[−3,0,−0.5]，对应的输出Y=[1,0,−1]T，设定η为1 ，同时激活函数约定为阶跃函数 sgn 。 而己知W1​=W0​+ΔW， 因此需要首先计算出ΔW，对于训练数据的第一组输入向量X：

通过上述计算即可得到第一组训练的输入X1​对应的权值调整，得到新的W!​之后，继续进行输入向量X2​和X3​调整权值即可。

最小均方规则

最小均方规则 （ Least Mean Square , LMS ） 也被称作 Widrow-Hoff 学习规则，基本原理是对一组包含 n个元素的x1​,x2​,…,xn​的输入作为一个线性组合加权求和，对得到的求和结果 y 与期望输出 d进行比较，计算误差值 e ，并根据误差值的大小对权值进行调整。
例如，设定对于 n个输入元素x1​,x2​,…,xn​都有 n个对应权值向量w1​,w2​,…,wn​，则加权求和的 y 可以按照如下公式计算 ：

最小均方规则是一种非常简单易懂的学习规则，它的学习方式与神经元的激活函数没有任何关系，也不需要对激活函数求导，不仅学习速度比较快，而且有一定的计算精度。

作答要求

根据相关知识，按照要求完成右侧选择题任务。作答完毕，通过点击“测评”，可以验证答案的正确性。

答案