R语言--模型的定阶、估计和显著性检验

在前面，我们介绍了平稳非白噪声的检验方法。这章我们是在平稳非白噪声的前提下，对模型进行定阶、估计和检验。 

模型的识别与定阶

①直观识别

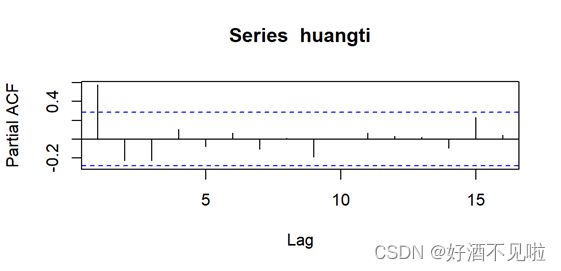
对于识别我们可以采用直观的识别方法，那就是通过自相关和偏自相关

acf(X,lag.max = )  #自相关图像
pacf(X,lag.max = )  #偏自相关图像

我们根据自相关和偏自相关所展示的图判断，如下：

 

上图分别为ACF和PACF图像 ，我们根据主观的判别法，可以看出ACF是呈现拖尾性，PACF呈现截尾性的。因此我们可以判别这是一个AR模型。接下来我们观察PACF所呈现的截尾是在滞后1阶处进行的截尾。因此，我们判断此模型为AR(1)。(关于MA模型的主观判别法放在最后了)

②扩展的自相关函数（三角格子法）

library(TSA)  #调用TSA包
eacf(X)       #画出扩展自相关图

我们看下图：

我们找到这个三角形，在三角形的角中找到“圆圈”，即模型为ARMA(0,0,1)。注ARMA(p,d,q),其中p为AR的阶数，d为差分，q为MA的阶数。

③BIC准则

library(forecast)    #调用预测包
auto.arima(x,max.p = 14,max.q = 14,ic="bic")  #我们通过BIC判别法进行模型的定阶，
#其中max.p和max.q为AR、MA的最大阶数。
#ic 有AIC BIC AICC 三个选项，系统默认AIC，这里我们可以选用bic

 我们通过bic的自动识别最优阶数对模型进行定阶，如下图（一个例子，供大家参考）：

图中，我们能够看到，系统给出的定阶模型为ARIMA(1,0,0)。与此同时，我们可以看一下系统所定阶的模型的参数ar1 = 0.5739远远大于它的2倍标准误差（s.e. = 0.1161）,故我们可以判断我们的参数显著非零。因此，我们肯定了该系统给出的模型和阶数。

④armasubset()

关于armasubset()函数，也是一种定阶的方法。因为前面文章中，对它有单独的介绍，故这里就不再多说了

res = armasubsets(X,nar = 14，nma = 14,ar.method = "ols")
#X为待拟合的时间序列，nar为AR的最大阶数，nma为MA的最大阶数
#ar.method = "ols",表示AR部分的拟合方法是最小二乘法

plot(res)  

参数估计

前面我们对模型进行识别和定阶之后，我们选出我们识别出模型以及其模型的阶数c(p,d,q)各是多少，然后对模型进行参数估计。

fit1 = arima(X,order = c(1,1,1),include.mean = T,method = "ML")
fit1
#X为时间序列
#order为我们所定阶的模型 c(p,d,q)
#include.mean = T时，模型中需要均值，F为不需要
#method为指定的参数估计方法：CSS-   ML   CSS-ML 
#三种方法分别为条件最小二乘法、极大似然估计以及两者的混合方法

模型的显著性检验

进行模型的显著性检验时，我们需要了解它检验的是什么？

模型的检验主要检验模型的有效性，而一个模型是否有效主要是看它提取信息是否充分，如何看一个信息提取是否充分呢，我们就看它的残差序列。如果残差序列中还残留着相关信息未被提取，那么说明拟合的模型不够有效。

因此，模型的显著性检验，就是观察我们的残差序列是不是白噪声。是白噪声即模型有效。

library(aTSA)
ts.diag(X)

怎么通过这四张图判断是否是白噪声呢，如下图：

左上图为残差序列自相关图。

右上图为残差序列的偏自相关图。

左下图为残差序列的白噪声图。其横轴为延迟阶数，我们从图中可以看出其Q统计量的P值都在0.05(红色虚线)显著参考线之上，认为是白噪声序列。即我们认为该模型是显著成立的。

右下图为残差序列正态性检验的QQ图，从该图中我们认为残差部分近似服从正态分布。

(基本上我们看左下角这张图就可以判断其是否为白噪声了)

补充

我们通过ACF、PACF的图像去怎么判断MA模型呢？我们要清楚：

AR(p)模型是ACF呈拖尾，PACF呈p阶截尾

MA(q)模型是ACF呈q阶截尾，PACF呈拖尾

ARMA模型是ACF呈拖尾，PACF呈拖尾，这个时候我们就需要通过其它方式去给ARMA定阶了。

上一章我们介绍了平稳非白噪声的检验，这一章我们介绍了模型的识别、定阶、参数估计、模型的检验，下一章会推出建立模型的最后一个环节---参数的显著性检验、模型优化以及序列预测。