AI人工智能（调包侠）速成之路十（AlphaZero代码实战2：蒙特卡洛树搜索）

蒙特卡罗方法（Monte Carlo method）

什么是蒙特卡罗方法
        用通过概率实验所求的概率估计来估计一个未知量，这样的方法统称为蒙特卡罗方法（Monte Carlo method）。

为什么需要蒙特卡洛方法
        在现实世界中，大量存在一些复杂性过程，由于这类模型含有不确定的随机因素，我们很难直接用一个确定性模型来分析和描述。面对这种情况．数据科学家难以作定量分析，得不到解析的结果，或者是虽有解析结果，但计算代价太大以至不能使用。在这种情况下，可以考虑采用 Monte Carlo 方法。

蒙特卡洛方法的思想
        如果我们将宇宙中的每个事物都抽象为表象和里像这两种表现形式，里像是我们不可知的，只有上帝才知道，但是表象是我们可以通过物理手段观测得到的，而连接里像和表象的元定理就是因果律，因为因果律的存在，使得我们可以通过表象反推出里像，进而探问世界的真像。当因果律不太明确的时候，我们就通过大量的模拟统计来定量计算结果。

蒙特卡洛树搜索（Monte Carlo Tree Search，MCTS）算法

什么是蒙特卡罗树搜索方法
        蒙特卡洛树搜索说就是将蒙特卡洛方法这种随机模拟的方法应用到树搜索上。蒙特卡洛树搜索是一种基于树结构的蒙特卡洛方法，是一种确定规则驱动的启发式随机搜索算法。

为什么需要蒙特卡洛树搜索方法
        基本上程序员对树搜索都很熟悉，常用的是广度优先搜索和深度优先搜索，但是AlphaZero系统下围棋的时候要搜索的局面状态有多少种呢？我们可以简单估算下数量级。围棋盘面上有19*19=361个点，每个落子点只存在三种可能（黑、白、空），因此盘面的上限为3的361次方种。如果按照300步来计算对弈一盘棋要遇到的局面选择，第一步为361种可能性，第二步为360，第三步为359······所以总数为361!（阶乘），这个数字大约等于1.73E+686。宇宙中原子总数为1.67E+80。所以人类对弈围棋的时候很多选择是根据经验排除了很多选项，然后少数几个选择里靠“直觉”加估计一个更有利的选择。蒙特卡洛树搜索就是要模拟这个过程，先选择几个大的先验概率方向搜索，然后按先验概率模拟对弈到结束，再通过对弈结果给出的奖励信号反向传播更新局面估值，最后选择一个估值有利的局面。

MCTS的5个主要核心部分：

• 树结构：树结构定义了一个可行解的解空间，每一个叶子节点到根节点的路径都对应了一个解（solution），解空间的大小为2N（N等于决策次数，即树深度）
• 蒙特卡洛方法：MSTC不需要事先给定打标样本，随机统计方法充当了驱动力的作用，通过随机统计实验获取观测结果。
• 损失评估函数：有一个根据一个确定的规则设计的可量化的损失函数（目标驱动的损失函数），它提供一个可量化的确定性反馈，用于评估解的优劣。从某种角度来说，MCTS是通过随机模拟寻找损失函数代表的背后”真实函数“。
• 反向传播线性优化：每次获得一条路径的损失结果后，采用反向传播（Backpropagation）对整条路径上的所有节点进行整体优化，优化过程连续可微
• 启发式搜索策略：算法遵循损失最小化的原则在整个搜索空间上进行启发式搜索，直到找到一组最优解或者提前终止

算法的优化核心思想总结一句话就是：在确定方向的渐进收敛（树搜索的准确性）和随机性（随机模拟的一般性）之间寻求一个最佳平衡。体现了纳什均衡的思想精髓。

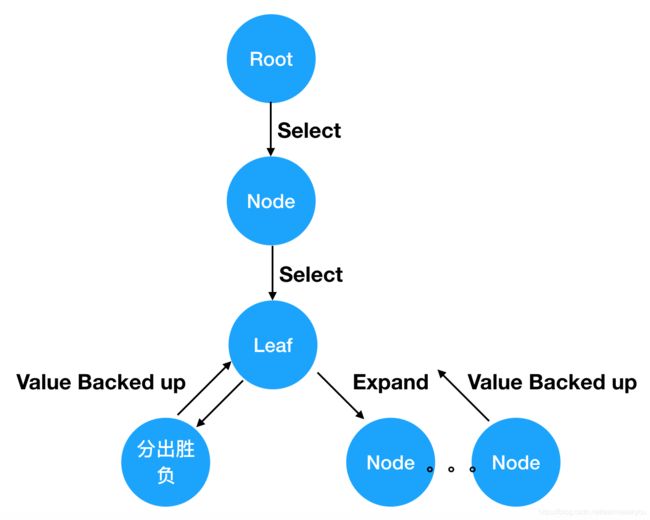
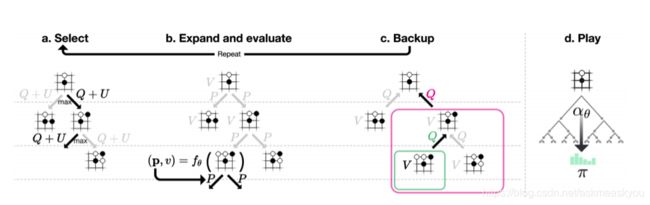
MCTS搜索就是建立一棵树的过程。蒙特卡罗树搜索大概可以被分成四步。选择(Selection)，拓展(Expansion)，模拟(Simulation)，反向传播(Backpropagation)。下面我们结合一个五子棋AI的案例代码逐个来分析。

建立一棵树

class TreeNode:
    """
    蒙特卡洛树的一个节点，每个节点存了Q值，P值，N值
    """

    def __init__(self, parent, prior_p):
        self._parent = parent
        self._children = {}  # 键是动作值，值是节点
        self._n_visits = 0
        self._Q = 0
        self._P = prior_p

MCTS本质上是我们来维护一棵树，这棵树的每个节点保存了每一个局面（situation）该如何走子（action）的信息。这些信息是，N(s, a)是访问次数，W(s, a)是总行动价值，Q(s, a)是平均行动价值，P(s, a)是被选择的概率。

选择(Selection)

    def select(self, c_puct):
        """
        选择所有子节点中Q+u(P)最大的返回。
        :param c_puct: 一个在范围(0, inf)的值，控制Q和P的比例
        :return: 二元组(action, next_node)
        """
        return max(self._children.items(), key=lambda act_node: act_node[1].get_value(c_puct))

    def get_value(self, c_puct):
        """
        得到该节点的Q+u(P)值
        :param c_puct: 一个在范围(0, inf)的值，控制Q和P的比例
        :return: 该节点的Q+u(P)值
        """
        u = c_puct * self._P * np.sqrt(self._parent._n_visits) / (1 + self._n_visits)
        return self._Q + u

每次模拟的过程都一样，从父节点的局面开始，选择一个走子。比如开局的时候，所有合法的走子都是可能的选择，那么我该选哪个走子呢？这就是select要做的事情。MCTS选择Q(s, a) + U(s, a)最大的那个action。c_puct是一个决定探索水平的常数；这种搜索控制策略最初倾向于具有高先验概率和低访问次数的行为，但是渐近地倾向于具有高行动价值的行为。

拓展(Expansion)

    def expand(self, action_priors):
        """
        展开一个叶子节点。
        :param action_priors: 一个元素为(action, P)的列表
        """
        for action, prob in action_priors:
            if action not in self._children:
                self._children[action] = TreeNode(self, prob)

我们要接着上个局面选择action，但是这个局面是个叶子节点。就是说之后可以选择哪些action不知道，这样就需要expand了，通过expand得到一系列可能的action节点。这样实际上就是在扩展这棵树，从只有根节点开始，一点一点的扩展。这个时候要用我们的神经网络出马。把当前的局面作为输入传给神经网络，神经网络会返回给我们一个action向量p和当前胜率v。其中action向量是当前局面每个合法action的走子概率。这样在当前局面下，所有可走的action以及对应的概率p就都有了。当然，神经网络还没有训练好，一开始给出的都是随机值，之后通过不断的训练，神经网络给出的估值会越来越好。

模拟(Simulation)

class MCTS:
    """
    蒙特卡洛树及其搜索方法。
    """

    def __init__(self, policy_value_fn, c_puct=5, n_playout=300):
        """
        :param policy_value_fn: 论文里面的(p,v)=f(s)函数。接受一个board作为参数并返回一个（动作，概率）列表和在[-1, 1]范围的局面胜率的函数
        :param c_puct: 论文里面的c_puct。一个在范围(0, inf)的数字，控制探索等级。值越小越依赖于Q值，值越大越依赖于P值
        :param n_playout: 找MCTS叶子节点次数，即每次搜索次数
        """
        self._root = TreeNode(None, 1.0)
        self._policy = policy_value_fn
        self._c_puct = c_puct
        self._n_playout = n_playout

    def _playout(self, state):
        """
        执行一次蒙特卡洛搜索，找到一个叶子节点，并更新路径上所有节点的值。
        :param state: 一个Board对象，在搜索过程中这个Board对象的状态会随之改变，所以这个参数传进来前需要复制一份。
        """
        node = self._root
        while not node.is_leaf():  # 找到一个叶子节点
            action, node = node.select(self._c_puct)
            state.do_move(action)

        action_probs, leaf_value = self._policy(state)  # 得到一个相对于当前玩家的(action, probability)列表和在范围[-1, 1]的V值

        end, winner = state.game_end()  # 检查游戏是否结束
        if not end:
            node.expand(action_probs)
        else:
            if winner == -1:  # 平局V值为0
                leaf_value = 0.0
            else:
                leaf_value = (1.0 if winner == state.get_current_player() else -1.0)  # 当前玩家赢了V值为1，输了V值为-1

        # 更新路径上所有节点的值
        node.update_recursive(-leaf_value)

模拟自我对弈的过程。模拟结束后，基本上能覆盖大多数高先验概率的棋局和着法，每步棋该怎么下，下完以后胜率是多少，得到什么样的局面都能在树上找到。然后从树上选择当前局面应该下哪一步棋，当模拟结束后，对于当前局面（就是树的根节点）的所有子节点就是每一步对应的action节点，选择访问计数大的行为。然后从多个action中选一个，这其实是多分类问题。

反向传播(Backpropagation)

    def update(self, leaf_value):
        """
        根据叶子节点的V值更新本节点的N值和Q值。
        :param leaf_value: 从当前玩家视角的子树评估值
        """
        self._n_visits += 1
        self._Q += (leaf_value - self._Q) / self._n_visits

任意一个局面（就是节点），要么被展开过（expand），要么没有展开过（就是叶子节点）。展开过的节点可以使用Select选择动作进入下一个局面，叶子节点就继续展开。下一个局面仍然是这个过程，如果展开过还是可以通过Select进入下下个局面，这个过程一直持续下去直到这盘棋分出胜平负了为止。就是说我现在下了一步棋，不管这步棋是好棋还是臭棋，只有下完整盘期分出胜负，才能给我下的这步棋评分。然后把评分从终局逐层向上返回。

 

        至此MCTS算法就分析完了。AlphaZero巧妙了使用MCTS搜索树和神经网络一起，通过MCTS搜索树优化神经网络参数，反过来又通过优化的神经网络指导MCTS搜索。两者一主一辅，非常优雅的解决了这类状态完全可见，信息充分的棋类问题。我们在下一篇讨论给局面状态打分的神经网络如何实现。

 

AlphaZero代码实战系列 源代码打包
下载地址：https://download.csdn.net/download/askmeaskyou/12931806