斯坦福 算法1 第三周笔记

来自斯坦福网站的Algorithms: Design and Analysis，与目前coursera上的版本内容没有变化，不过时间安排略有不同。

1 LINEAR-TIME SELECTION

selection问题指的是，给定一个长度为n的无序数组，选取其中第k大的数。为了分析简单假定每个数字不重复。

1.1 randomized selection

1.1.1 算法

简单的方法可以直接将数组排序选取第k个数作为输出。但还有更简单的方式，可以回忆快排partition的操作：partition操作结束后，数组分为左边，右边以及pivot三个部分。因此第k个数的分布也对应三种情况。于是利用递归我们就得到了一个选择第k大的数的随机选择的算法：

1.1.2 正确性

可以利用归纳法证明算法的正确性，证明过程与快排时的证明类似：

• 当n=1时，算法能正确得到第k大的数。
• 假设当n=k1,k2时算法能得到第k大的数。因此在n=k3=k1(左边长度)+k2(右边长度)+1(pivot)时，如果k<=k1，则相当于是n=k1时，显然成立。如果k = k1+1则选到pivot。如果k>k1+1，相当于是n=k2时的情况，也是成立的。因此算法正确性得证。

1.1.3 复杂度分析

算法的运行时间一定程度上依然依赖于pivot的选择。比如如果是最坏的情况（已排序的数组，每次第一个作为pivot），运行时间依然是$O(n^2)$。但是假如pivot选得足够好，能够利用master method的话，那么可以得到这个算法的运行时间是$O(n)$。

事实上，这个算法的平均情况下运行时间是$O(n)$。

证明如下：由于每次递归剩下的数组长度无法得知，因此不好使用类似快排里证明的方法。这里使用了一个新的形式，定义了一个phase j，每个phase表示当前剩下的数组长度所在的长度范围为(${\frac{3}{4}}^{j+1}n,{\frac{3}{4}}^{j}n)$之间。

其中$X_j$表示在phase j里进行了几次调用。可以先重点计算一下这个变量的期望$E[X_j]$。考虑每次递归调用时的情景：假如我们的pivot选择在25%分位到75%分位数之间，那么下一次的调用时数组长度必然小于当前数组长度的$\frac{3}{4}$，也就是必然进入下一个phase。也就是说每次调用有50%的概率从当前phase j进入下一个phase。于是$E[X_j]$等同于求掷硬币得到正面时投掷次数的期望值，求得为2。

因此整个算法的平均复杂度为：

1.2 Deterministic Selection

随机性算法中我们期望得到一个较好的pivot，而每次最好的pivot自然是中位数。这似乎陷入了一个循环问题，比较找到第n/2大的数就是我们要做的问题。不过我们依然有办法得到一个足够好的pivot，这就是deterministic selection方法。

1.2.1 算法流程

这个算法选择pivot的方式很特别，那就是先将n个数按5个一组分成n/5组，然后取每组的中位数（用其它排序方法比如归并），之后再取这n/5个数的中位数作为pivot（递归调用selection函数）。选择了pivot之后的过程与上面随机的算法相同。

于是整个算法如下：

来分析每一步的复杂度。第一部分（1.）的复杂度就是$\Theta (n)$的。因为有n/5个数组，每个进行排序的时间是常数级别，因此总时间是$\Theta (n)$。其它部分如下所示：

只有最后两步不清楚时间，因为其数组长度未知。不过实际上可以证明，6,7两步中的数组长度一定落在[0.3n,0.7n]之间。这就是因为选择pivot的特殊操作导致的。其实仔细想想不难得出答案。图形化的证明如下：

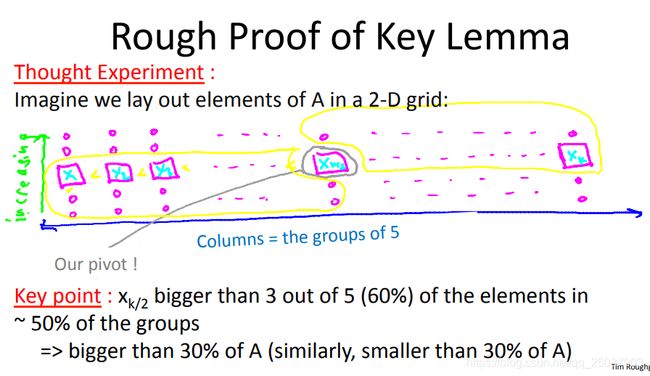
把每个小数组写为一列，共有n/5列。其中左下角必然比pivot小，即1/2*3/5 = 0.3，同理右上角比如比pivot大。于是得到最后两步递归时数组大小必然小于0.7n。也就是最终的运行时间有如下不等式：

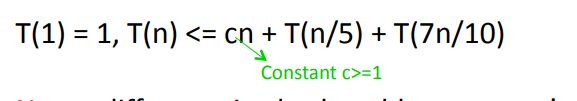
假设$T(n)=O(n)$，设一个常数a=10c，可以用归纳法做如下证明：

1.3 基于comparison的排序算法复杂度下限

定理：每个基于comparison的排序算法最坏的运行时间是$\Omega (nlogn)$。

基于camparison的排序是指只利用两个数互相比较来判断各自的大小从而排序。常见的有归并排序，快排和堆排序。而反例有桶排序，计数排序和radix排序。

定理的证明利用了鸽笼原理（背包原理？）。

• 假设有个长度为n的数组，那么这个数组中数字的排列有$n!$种。
• 假设算法最多进行k次比较就可以将这$n!$种排列进行排序。
• 而k次比较产生的序列以及对应的操作最多有$2^k$种。（长度为k的0101的序列，0或1对应不同的操作，比如交换位置等等。）
• 假如这$2^k$种序列小于$n!$，就会产生两个不同排序的数组进行了相同的操作序列的情况，不同的数组进行完全相同的操作显然不可能得到正确的排序结果。
• 因此$2^k\ge n!\ge {\frac{n}{2}}^{\frac{n}{2}}$，即$k\ge \Omega (nlogn)$

2 最小割的压缩算法

2.1 问题描述

图由点集与边集合构成。分为无向图与有向图。

图的割是指一个图分为非空的A和B两个点集的分割。一个有n个点的图最多有$2^n$个割。而一个割cut(A,B)的交叉边在无向图中表示两端分别在A和B中的边，而在有向图中的交叉边指的是尾部在A而指向集合B中点的边。

而最小割问题指的是，输入一个无向图G=(V,E)，输出一个交叉边数量最少的割。如图所示：

这个算法在图的分析，社交网络和图像分割等等领域有很多应用。

图分为有向图与无向图，区别在于边是否有方向。而又有稀疏图与稠密图。稀疏图指的是边的数量m接近点数量n的线性级别的图。而稠密图是指m接近$\Theta (n^2)$的图。

图可以用邻接矩阵表示。用一个nxn的矩阵表示每两个点之间的关系，每个矩阵的取值可以使(-1,0,1）代表方向或表示边的数量或是边的权值。

图也可以用邻接表表示。邻接表有几个部分组成：

它的空间复杂度是$O(m+n)$。在本门课里主要利用邻接表。

2.2 随机压缩算法

这个算法的想法很简单，每次选取一条边，将它们两端的点合并为一个点，去掉可能存在的自环直到只剩下两个点为止。

2.3 算法分析

这样的算法显然不可能每次都能够得到正确的最小割。但是可以计算一下这么做能够得到最小割的概率。问题的设定如下，重点是交叉边的定义：

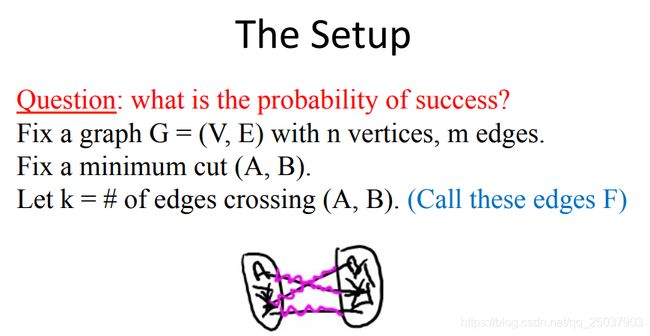
如果最后的结果是正确的，那么就需要每次选择边的时候都不选择这k条交叉边直到结束。可以将其写为一个随机事件：

其中$S_i$表示第i次选择边时选择到了F中的k条交叉边之一。于是整个时间就是他们补集的交。

可以很轻易的得到第一次选择时$Pr[S_1]$的概率是$\frac{k}{m}$，但这无法一只用来计算。因为每次迭代时减少的可能不止一条边（存在去掉自环的操作）。而相对的，每次肯定确定减少一个点，因此考虑用点的数量n来表示这个概率：

点数量n与边数量m以及最小割的交叉边数量k存在一定关系。因为每个点都对应一个割，而最小割的交叉边数量是k，因此每个点的度的和$2m\ge kn$，因此$m\ge kn/2$，即$Pr[S_1]\le 2/n$。

重复这个过程，我们发现每一次选择时都可以将概率写为用n表示的形式：

最终我们得到了整个事件的概率：

也就是说每次算法运行的成功率仅仅大于$1/n^2$。但是我们可以进行N次独立重复实验取交叉边最小的一次作为结果，而这N次独立重复实验有一次能成功的概率表示如下：

因此我们只需要进行足够多次的实验就能得到足够好的正确率保证。

2.4 最小割计数

我们知道一个树的最小割可以是n-1个，那么一个有n个点的图最多能够拥有多少个最小割呢？结果是$n(n-1)/2$，下面证明。

首先举个例子证明其下限：

因此这个最大值大于等于n(n-1)/2。

然后计算它的上限。假设一个图中存在数量为t的不同的最小割。那么每次算法运行精确得到某个最小割cut($A_i,B_i)$的概率是大于2/(n(n-1))的。而得到这t个不同的最小割是独立的事件，它们的概率可以相加，因此得到上限：

得证。