线性回归——二维线性回归方程(证明和代码实现)
前言:
前面一章推导了一下常用的几个距离公式,今天要来说一下机器学习中非常常用的一个算法,线性回归,这篇文章主要讲述的是二维情况下的线性回归问题.写这篇文章的目的有三个:一是利用平台做一次笔记;二是通过自己的理解看能够把这个知识点讲清楚也是判断自己是否掌握了;三是为后面有需要的小伙伴提供一个参考吧.不啰嗦了,开始进入正题:
一、原理讲述
-
这个应该上过高中的小伙伴都听过,也都用过,那是在高中必修3中出现的知识点,考试也是会考的,可能你想不起那个公式了,但你肯定依稀的记得 a ^ , b ^ \hat{a},\hat{b} a^,b^这两个东西,还有这个方程 y ^ = b ^ x + a ^ \hat{y}=\hat{b}x+\hat{a} y^=b^x+a^,通过这个方程来预测y的值, a ^ , b ^ \hat{a},\hat{b} a^,b^都有它们的计算方式,但是公式有点复杂,老师可能也说过一般试卷上会给,让我们在脑海来重温一下那个知识,这里先给出计算公式:
{ b ^ = ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ∑ i = 1 n ( x i − x ˉ ) 2 = ∑ i = 1 n x i y i − n x ˉ y ˉ ∑ i = 1 n x i 2 − n x ˉ 2 a ^ = y ˉ − b ^ x ˉ y ^ = b ^ x + a ^ \begin{cases} \displaystyle \hat{b}=\frac{\displaystyle \sum_{i=1}^n{(x_i-\bar{x})(y_i-\bar{y})}} {\displaystyle \sum_{i=1}^n{(x_i-\bar{x})^2}} =\frac{\displaystyle \sum_{i=1}^n{x_iy_i-n\bar{x}\bar{y}}} {\displaystyle \sum_{i=1}^n{x_i^2-n\bar{x}^2}} \\ \displaystyle \hat{a}=\bar{y}-\hat{b}\bar{x}\end{cases} \\ \hat{y}=\hat{b}x+\hat{a} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧b^=i=1∑n(xi−xˉ)2i=1∑n(xi−xˉ)(yi−yˉ)=i=1∑nxi2−nxˉ2i=1∑nxiyi−nxˉyˉa^=yˉ−b^xˉy^=b^x+a^
公式够复杂,但是看着公式里面需要的参数来说其实也没有什么难度,其中公式中最重要的两个参数就是 x ˉ , y ˉ \bar{x},\bar{y} xˉ,yˉ也就分别是x,和y的平均值,计算很简单.我们要学习一个东西既要知其然也要知其所以然,不妨我们从头来推导出这个公式: -
首先我假设 x , y x,y x,y为两个具有线性关系的变量,而且我们经有了回归方程模型 y ^ = b ^ x + a ^ \hat{y}=\hat{b}x+\hat{a} y^=b^x+a^,而且现在还有一组原始值(就是训练数据): ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ⋯ , ( x n − 1 , y n − 1 ) , ( x n , y n ) (x_1,y_1),(x_2,y_2),\cdots,\cdots,(x_{n-1},y_{n-1}),(x_n,y_n) (x1,y1),(x2,y2),⋯,⋯,(xn−1,yn−1),(xn,yn),现在我们要通过我们得到的这个模型来计算出预测值,通过想模型中填入训练数据的所有 x i x_i xi的值, 我们又可以得到一组预测数据: ( x 1 , y ^ 1 ) , ( x 2 , y ^ 2 ) , ( x n − 1 , y ^ n − 1 ) , ( x n , y ^ n ) (x_1,\hat{y}_1),(x_2,\hat{y}_2),(x_{n-1},\hat{y}_{n-1}),(x_n,\hat{y}_n) (x1,y^1),(x2,y^2),(xn−1,y^n−1),(xn,y^n),现在我们要来计算训练数据与真实数据之间的拟合度,如果我们利用下面这个公式来计算拟合度看看会发生什么:
λ = ∑ i = 1 n ( y i − y ^ i ) \displaystyle \color{Red} \lambda=\sum_{i=1}^n{(y_i-\hat{y}_i)} λ=i=1∑n(yi−y^i)
很明显这样是错误的,因为我们预测值和真实值的波动是上下波动的,也就是说误差值可正可负,那么如果我们只有两组测试数据, y 1 y_1 y1与 y ^ 1 \hat{y}_1 y^1 之差为 -5, y 2 y_2 y2与 y ^ 2 \hat{y}_2 y^2 之差为 +5,那么通过这个公式一计算你会发现误差为0,也就是说预测值和真实值是完全拟合的,但是通过我们人去看显然波动非常大.所以我们得改进一下公式变为这样:
λ = ∑ i = 1 n ( y i − y ^ i ) 2 \displaystyle \lambda=\sum_{i=1}^n{(y_i-\hat{y}_i)^2} λ=i=1∑n(yi−y^i)2
这样一来就算是负的误差通过平方后也会变成正的,所以在叠加时也不会出现正负抵消的情况了.
再推导线性回归方程前我们先来证明一上面求 b ^ \hat{b} b^为什么可以这样变形,也就是下面两个等式为什么成立(因为这两个等式在推导线性回归方程时会用到): -
等式一: ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) = ∑ i = 1 n x i y i − n x ˉ y ˉ \displaystyle \sum_{i=1}^n{(x_i-\bar{x})(y_i-\bar{y})}=\displaystyle \sum_{i=1}^n{x_iy_i-n\bar{x}\bar{y}} i=1∑n(xi−xˉ)(yi−yˉ)=i=1∑nxiyi−nxˉyˉ
证明:
将等式左边展开
= ( x 1 − x ˉ ) ( y 1 − y ˉ ) + ( x 2 − x ˉ ) ( y 2 − y ˉ ) + ⋯ + ( x n − x ˉ ) ( y n − y ˉ ) =(x_1-\bar{x})(y_1-\bar{y})+(x_2-\bar{x})(y_2-\bar{y})+\cdots+(x_n-\bar{x})(y_n-\bar{y}) =(x1−xˉ)(y1−yˉ)+(x2−xˉ)(y2−yˉ)+⋯+(xn−xˉ)(yn−yˉ)= ( x 1 y 1 − x 1 y ˉ − x ˉ y 1 + x ˉ y ˉ ) + ( x 2 y 2 − x 2 y ˉ − x ˉ y 2 + x ˉ y ˉ ) + ⋯ + ( x n y n − x n y ˉ − x ˉ y n + x ˉ y ˉ ) =(x_1y_1-x_1\bar{y}-\bar{x}y_1+\bar{x}\bar{y})+(x_2y_2-x_2\bar{y}-\bar{x}y_2+\bar{x}\bar{y})+\cdots+(x_ny_n-x_n\bar{y}-\bar{x}y_n+\bar{x}\bar{y}) =(x1y1−x1yˉ−xˉy1+xˉyˉ)+(x2y2−x2yˉ−xˉy2+xˉyˉ)+⋯+(xnyn−xnyˉ−xˉyn+xˉyˉ)
合并同类项:
= ( x 1 y 1 + x 2 y 2 + ⋯ + x n y n ) − ( x 1 y ˉ + x 2 y ˉ + ⋯ + x n y ˉ ) − ( x ˉ y 1 + x ˉ y 2 + ⋯ + x ˉ y n ) + n x ˉ y ˉ =(x_1y_1+x_2y_2+\cdots+x_ny_n)-(x_1\bar{y}+x_2\bar{y}+\cdots+x_n\bar{y})-(\bar{x}y_1+\bar{x}y_2+\cdots+\bar{x}y_n)+n\bar{x}\bar{y} =(x1y1+x2y2+⋯+xnyn)−(x1yˉ+x2yˉ+⋯+xnyˉ)−(xˉy1+xˉy2+⋯+xˉyn)+nxˉyˉ= ∑ i = 1 n x i y i − n y ˉ ( x 1 + x 2 + ⋯ + x n n ) − n x ˉ ( y 1 + y 2 + ⋯ + y n n ) + n x ˉ y ˉ =\displaystyle \sum_{i=1}^n{x_iy_i}-n\bar{y}(\frac{x_1+x_2+\cdots+x_n}{n})-n\bar{x}(\frac{y_1+y_2+\cdots+y_n}{n})+n\bar{x}\bar{y} =i=1∑nxiyi−nyˉ(nx1+x2+⋯+xn)−nxˉ(ny1+y2+⋯+yn)+nxˉyˉ
∵ x ˉ , y ˉ \bar{x},\bar{y} xˉ,yˉ分别代表所有变量x和y的平均值
∴原式 = ∑ i = 1 n x i y i − n x ˉ y ˉ − n x ˉ y ˉ + n x ˉ y ˉ =\displaystyle \sum_{i=1}^n{x_iy_i}-n\bar{x}\bar{y}-n\bar{x}\bar{y}+n\bar{x}\bar{y} =i=1∑nxiyi−nxˉyˉ−nxˉyˉ+nxˉyˉ
= ∑ i = 1 n x i y i − n x ˉ y ˉ = =\displaystyle \sum_{i=1}^n{x_iy_i-n\bar{x}\bar{y}}= =i=1∑nxiyi−nxˉyˉ=等式右端
证闭
-
等式二:
∑ i = 1 n ( x i − x ˉ ) 2 = ∑ i = 1 n x i 2 − n x ˉ 2 \displaystyle \sum_{i=1}^n{(x_i-\bar{x})^2}=\displaystyle \sum_{i=1}^n{x_i^2-n\bar{x}^2} i=1∑n(xi−xˉ)2=i=1∑nxi2−nxˉ2证明:
将等式左边展开
= ( x 1 − x ˉ ) 2 + ( x 2 − x ˉ ) 2 + ⋯ + ( x n − x ˉ ) 2 =(x_1-\bar{x})^2+(x_2-\bar{x})^2+\cdots+(x_n-\bar{x})^2 =(x1−xˉ)2+(x2−xˉ)2+⋯+(xn−xˉ)2= ( x 1 2 − 2 x 1 x ˉ + x ˉ 2 ) + ( x 2 2 − 2 x 2 x ˉ + x ˉ 2 ) + ⋯ + ( x n 2 − 2 x n x ˉ + x ˉ 2 ) =(x_1^2-2x_1\bar{x}+\bar{x}^2)+(x_2^2-2x_2\bar{x}+\bar{x}^2)+\cdots+(x_n^2-2x_n\bar{x}+\bar{x}^2) =(x12−2x1xˉ+xˉ2)+(x22−2x2xˉ+xˉ2)+⋯+(xn2−2xnxˉ+xˉ2)
合并同类项
= ( x 1 2 + x 2 2 + ⋯ + x n 2 ) − 2 x ˉ ( x 1 + x 2 + ⋯ + x n ) + n x ˉ 2 =(x_1^2+x_2^2+\cdots+x_n^2)-2\bar{x}(x_1+x_2+\cdots+x_n)+n\bar{x}^2 =(x12+x22+⋯+xn2)−2xˉ(x1+x2+⋯+xn)+nxˉ2= ∑ i = 1 n x i 2 − 2 n x ˉ ( x 1 + x 2 + ⋯ + x n n ) + n x ˉ 2 =\displaystyle \sum_{i=1}^n{x_i^2} - 2n\bar{x}(\frac{x_1+x_2+\cdots+x_n}{n})+n\bar{x}^2 =i=1∑nxi2−2nxˉ(nx1+x2+⋯+xn)+nxˉ2
= ∑ i = 1 n x i 2 − 2 n x ˉ 2 + n x ˉ 2 =\displaystyle \sum_{i=1}^n{x_i^2} - 2n\bar{x}^2+n\bar{x}^2 =i=1∑nxi2−2nxˉ2+nxˉ2
= ∑ i = 1 n x i 2 − n x ˉ 2 = =\displaystyle \sum_{i=1}^n{x_i^2} - n\bar{x}^2= =i=1∑nxi2−nxˉ2=等式右端
证闭
-
推导线性回归方程:
有了前面两个等式现在我们就可以来推导回归方程的来龙去脉了.
证明:
∵ λ = ∑ i = 1 n ( y i − y ^ i ) 2 , y ^ = b ^ x + a ^ \displaystyle \lambda=\sum_{i=1}^n{(y_i-\hat{y}_i)^2},\hat{y}=\hat{b}x+\hat{a} λ=i=1∑n(yi−y^i)2,y^=b^x+a^∴ λ = ∑ i = 1 n ( y i − b ^ x i − a ^ ) 2 \displaystyle \lambda=\sum_{i=1}^n{(y_i-\hat{b}x_i-\hat{a})^2} λ=i=1∑n(yi−b^xi−a^)2
展开得:
λ = ( y 1 − b ^ x 1 − a ^ ) 2 + ( y 2 − b ^ x 2 − a ^ ) 2 + ⋯ + ( y n − b ^ x n − a ^ ) 2 \lambda=(y_1-\hat{b}x_1-\hat{a})^2+(y_2-\hat{b}x_2-\hat{a})^2+\cdots+(y_n-\hat{b}x_n-\hat{a})^2 λ=(y1−b^x1−a^)2+(y2−b^x2−a^)2+⋯+(yn−b^xn−a^)2= [ y 1 − ( b ^ x 1 + a ^ ) ] 2 + [ y 2 − ( b ^ x 2 + a ^ ) ] 2 + ⋯ + [ y n − ( b ^ x n + a ^ ) ] 2 =[y_1-(\hat{b}x_1+\hat{a})]^2+[y_2-(\hat{b}x_2+\hat{a})]^2+\cdots+[y_n-(\hat{b}x_n+\hat{a})]^2 =[y1−(b^x1+a^)]2+[y2−(b^x2+a^)]2+⋯+[yn−(b^xn+a^)]2
= [ y 1 2 − 2 y 1 ( b ^ x 1 + a ^ ) ) + ( b ^ x 1 + a ^ ) ) 2 ] + [ y 2 2 − 2 y 2 ( b ^ x 2 + a ^ ) ) + ( b ^ x 2 + a ^ ) ) 2 ] + ⋯ + [ y n 2 − 2 y n ( b ^ x n + a ^ ) ) + ( b ^ x n + a ^ ) ) 2 ] =[y_1^2-2y_1(\hat{b}x_1+\hat{a}))+(\hat{b}x_1+\hat{a}))^2]+[y_2^2-2y_2(\hat{b}x_2+\hat{a}))+(\hat{b}x_2+\hat{a}))^2]+\cdots+[y_n^2-2y_n(\hat{b}x_n+\hat{a}))+(\hat{b}x_n+\hat{a}))^2] =[y12−2y1(b^x1+a^))+(b^x1+a^))2]+[y22−2y2(b^x2+a^))+(b^x2+a^))2]+⋯+[yn2−2yn(b^xn+a^))+(b^xn+a^))2]
= ( y 1 2 + y 2 2 + ⋯ + y n 2 ) − { [ 2 y 1 ( b ^ x 1 + a ^ ) − ( b ^ x 1 + a ^ ) 2 ] + ⋯ + [ 2 y n ( b ^ x n + a ^ ) − ( b ^ x n + a ^ ) 2 ] } =(y_1^2+y_2^2+\cdots+y_n^2)-\{[2y_1(\hat{b}x_1+\hat{a})-(\hat{b}x_1+\hat{a})^2]+\cdots+[2y_n(\hat{b}x_n+\hat{a})-(\hat{b}x_n+\hat{a})^2]\} =(y12+y22+⋯+yn2)−{[2y1(b^x1+a^)−(b^x1+a^)2]+⋯+[2yn(b^xn+a^)−(b^xn+a^)2]}
= ∑ i = 1 n y i 2 − { [ 2 y 1 ( b ^ x 1 + a ^ ) − ( b ^ x 1 + a ^ ) 2 ] + ⋯ + [ 2 y n ( b ^ x n + a ^ ) − ( b ^ x n + a ^ ) 2 ] } =\displaystyle \sum_{i=1}^n{y_i^2}-\{[2y_1(\hat{b}x_1+\hat{a})-(\hat{b}x_1+\hat{a})^2]+\cdots+[2y_n(\hat{b}x_n+\hat{a})-(\hat{b}x_n+\hat{a})^2]\} =i=1∑nyi2−{[2y1(b^x1+a^)−(b^x1+a^)2]+⋯+[2yn(b^xn+a^)−(b^xn+a^)2]}
= ∑ i = 1 n y i 2 − [ ( 2 b ^ y 1 x 1 + 2 a ^ y 1 − b ^ 2 x 1 2 − 2 a ^ b ^ x 1 − a ^ 2 ) + ⋯ + ( 2 b ^ y n x n + 2 a ^ y n − b ^ 2 x n 2 − 2 a ^ b ^ x n − a ^ 2 ) ] =\displaystyle \sum_{i=1}^n{y_i^2}-[(2\hat{b}y_1x_1+2\hat{a}y_1-\hat{b}^2x_1^2-2\hat{a}\hat{b}x_1-\hat{a}^2)+\cdots+(2\hat{b}y_nx_n+2\hat{a}y_n-\hat{b}^2x_n^2-2\hat{a}\hat{b}x_n-\hat{a}^2)] =i=1∑nyi2−[(2b^y1x1+2a^y1−b^2x12−2a^b^x1−a^2)+⋯+(2b^ynxn+2a^yn−b^2xn2−2a^b^xn−a^2)]
整理并合并同类项:
= ∑ i = 1 n y i 2 − 2 b ^ ∑ i = 1 n x i y i − 2 a ^ ∑ i = 1 n y i + b ^ 2 ∑ i = 1 n x i 2 + 2 a ^ b ^ ∑ i = 1 n x i + n a ^ 2 =\displaystyle \sum_{i=1}^n{y_i^2} -2\hat{b}\sum_{i=1}^n{x_iy_i}-2\hat{a}\sum_{i=1}^n{y_i}+\hat{b}^2\sum_{i=1}^n{x_i^2}+2\hat{a}\hat{b}\sum_{i=1}^n{x_i}+n\hat{a}^2 =i=1∑nyi2−2b^i=1∑nxiyi−2a^i=1∑nyi+b^2i=1∑nxi2+2a^b^i=1∑nxi+na^2
整理得:
= ∑ i = 1 n y i 2 − 2 n a ^ ( ∑ i = 1 n y i n − b ^ ∑ i = 1 n x i n ) − 2 b ^ ∑ i = 1 n x i y i + b ^ 2 ∑ i = 1 n x i 2 + n a ^ 2 =\displaystyle \sum_{i=1}^n{y_i^2}-2n\hat{a}\left(\frac{\displaystyle \sum_{i=1}^n{y_i}}{n}-\frac{\displaystyle \hat{b}\sum_{i=1}^n{x_i}}{n}\right)-2\hat{b}\sum_{i=1}^n{x_iy_i}+\hat{b}^2\sum_{i=1}^n{x_i^2}+n\hat{a}^2 =i=1∑nyi2−2na^⎝⎜⎜⎜⎜⎛ni=1∑nyi−nb^i=1∑nxi⎠⎟⎟⎟⎟⎞−2b^i=1∑nxiyi+b^2i=1∑nxi2+na^2= ∑ i = 1 n y i 2 − 2 n a ^ ( y ˉ − b ^ x ˉ ) − 2 b ^ ∑ i = 1 n x i y i + b ^ 2 ∑ i = 1 n x i 2 + n a ^ 2 =\displaystyle \sum_{i=1}^n{y_i^2}-2n\hat{a}\left(\bar{y}-\hat{b}\bar{x}\right)-2\hat{b}\sum_{i=1}^n{x_iy_i}+\hat{b}^2\sum_{i=1}^n{x_i^2}+n\hat{a}^2 =i=1∑nyi2−2na^(yˉ−b^xˉ)−2b^i=1∑nxiyi+b^2i=1∑nxi2+na^2
合并同类项:
= n [ a ^ 2 − 2 a ^ ( y ˉ − b ^ x ˉ ) ] + ∑ i = 1 n y i 2 − 2 b ^ ∑ i = 1 n x i y i + b ^ 2 ∑ i = 1 n x i 2 =\displaystyle n\left[\hat{a}^2 -2\hat{a}\left(\bar{y}-\hat{b}\bar{x}\right)\right]+ \sum_{i=1}^n{y_i^2}-2\hat{b}\sum_{i=1}^n{x_iy_i}+\hat{b}^2\sum_{i=1}^n{x_i^2} =n[a^2−2a^(yˉ−b^xˉ)]+i=1∑nyi2−2b^i=1∑nxiyi+b^2i=1∑nxi2
通过完全平方公式,对方括号内的元素进行配方:
= n [ a ^ 2 − 2 a ^ ( y ˉ − b ^ x ˉ ) + ( y ˉ − b ^ x ˉ ) 2 − ( y ˉ − b ^ x ˉ ) 2 ] + ∑ i = 1 n y i 2 − 2 b ^ ∑ i = 1 n x i y i + b ^ 2 ∑ i = 1 n x i 2 =\displaystyle n\left[\hat{a}^2 -2\hat{a}\left(\bar{y}-\hat{b}\bar{x}\right)+\left(\bar{y}-\hat{b}\bar{x}\right)^2-\left(\bar{y}-\hat{b}\bar{x}\right)^2\right]+ \sum_{i=1}^n{y_i^2}-2\hat{b}\sum_{i=1}^n{x_iy_i}+\hat{b}^2\sum_{i=1}^n{x_i^2} =n[a^2−2a^(yˉ−b^xˉ)+(yˉ−b^xˉ)2−(yˉ−b^xˉ)2]+i=1∑nyi2−2b^i=1∑nxiyi+b^2i=1∑nxi2= n [ a ^ − ( y ˉ − b ^ x ˉ ) ] 2 − n ( y ˉ − b ^ x ˉ ) 2 + ∑ i = 1 n y i 2 − 2 b ^ ∑ i = 1 n x i y i + b ^ 2 ∑ i = 1 n x i 2 =\displaystyle n\left[\hat{a}-\left(\bar{y}-\hat{b}\bar{x}\right)\right]^2-n\left(\bar{y}-\hat{b}\bar{x}\right)^2+ \sum_{i=1}^n{y_i^2}-2\hat{b}\sum_{i=1}^n{x_iy_i}+\hat{b}^2\sum_{i=1}^n{x_i^2} =n[a^−(yˉ−b^xˉ)]2−n(yˉ−b^xˉ)2+i=1∑nyi2−2b^i=1∑nxiyi+b^2i=1∑nxi2
展开第二项:
n [ a ^ − ( y ˉ − b ^ x ˉ ) ] 2 − n y ˉ 2 + 2 n b ^ x ˉ y ˉ − n b ^ 2 x ˉ 2 + ∑ i = 1 n y i 2 − 2 b ^ ∑ i = 1 n x i y i + b ^ 2 ∑ i = 1 n x i 2 \displaystyle n\left[\hat{a}-\left(\bar{y}-\hat{b}\bar{x}\right)\right]^2-n\bar{y}^2+2n\hat{b}\bar{x}\bar{y}-n\hat{b}^2\bar{x}^2+ \sum_{i=1}^n{y_i^2}-2\hat{b}\sum_{i=1}^n{x_iy_i}+\hat{b}^2\sum_{i=1}^n{x_i^2} n[a^−(yˉ−b^xˉ)]2−nyˉ2+2nb^xˉyˉ−nb^2xˉ2+i=1∑nyi2−2b^i=1∑nxiyi+b^2i=1∑nxi2整理一下:
= n [ a ^ − ( y ˉ − b ^ x ˉ ) ] 2 + ( ∑ i = 1 n y i 2 − n y ˉ 2 ) − ( 2 b ^ ∑ i = 1 n x i y i − 2 n b ^ x ˉ y ˉ ) + ( b ^ 2 ∑ i = 1 n x i 2 − n b ^ 2 x ˉ 2 ) =\displaystyle n\left[\hat{a}-\left(\bar{y}-\hat{b}\bar{x}\right)\right]^2+ \left(\sum_{i=1}^n{y_i^2}-n\bar{y}^2\right)-\left(2\hat{b}\sum_{i=1}^n{x_iy_i}-2n\hat{b}\bar{x}\bar{y}\right)+\left(\hat{b}^2\sum_{i=1}^n{x_i^2}-n\hat{b}^2\bar{x}^2\right) =n[a^−(yˉ−b^xˉ)]2+(i=1∑nyi2−nyˉ2)−(2b^i=1∑nxiyi−2nb^xˉyˉ)+(b^2i=1∑nxi2−nb^2xˉ2)
提取公因子:
= n [ a ^ − ( y ˉ − b ^ x ˉ ) ] 2 + ( ∑ i = 1 n y i 2 − n y ˉ 2 ) − 2 b ^ ( ∑ i = 1 n x i y i − n x ˉ y ˉ ) + b ^ 2 ( ∑ i = 1 n x i 2 − n x ˉ 2 ) =\displaystyle n\left[\hat{a}-\left(\bar{y}-\hat{b}\bar{x}\right)\right]^2+ \left(\sum_{i=1}^n{y_i^2}-n\bar{y}^2\right)-2\hat{b}\left(\sum_{i=1}^n{x_iy_i}-n\bar{x}\bar{y}\right)+\hat{b}^2\left(\sum_{i=1}^n{x_i^2}-n\bar{x}^2\right) =n[a^−(yˉ−b^xˉ)]2+(i=1∑nyi2−nyˉ2)−2b^(i=1∑nxiyi−nxˉyˉ)+b^2(i=1∑nxi2−nxˉ2)
代入等式一,等式二进行代换:
= n [ a ^ − ( y ˉ − b ^ x ˉ ) ] 2 + ∑ i = 1 n ( y i − y ˉ ) 2 − 2 b ^ ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) + b ^ 2 ∑ i = 1 n ( x i − x ˉ ) 2 =\displaystyle n\left[\hat{a}-\left(\bar{y}-\hat{b}\bar{x}\right)\right]^2+ \sum_{i=1}^n{\left({y_i}-\bar{y}\right)^2}-2\hat{b}\displaystyle \sum_{i=1}^n{(x_i-\bar{x})(y_i-\bar{y})}+\hat{b}^2\displaystyle \sum_{i=1}^n{(x_i-\bar{x})^2} =n[a^−(yˉ−b^xˉ)]2+i=1∑n(yi−yˉ)2−2b^i=1∑n(xi−xˉ)(yi−yˉ)+b^2i=1∑n(xi−xˉ)2
合并变换:
= n [ a ^ − ( y ˉ − b ^ x ˉ ) ] 2 + ∑ i = 1 n ( y i − y ˉ ) 2 + ∑ i = 1 n ( x i − x ˉ ) 2 [ b ^ 2 − 2 b ^ ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ∑ i = 1 n ( x i − x ˉ ) 2 ] =\displaystyle n\left[\hat{a}-\left(\bar{y}-\hat{b}\bar{x}\right)\right]^2+ \sum_{i=1}^n{\left({y_i}-\bar{y}\right)^2}+\displaystyle \sum_{i=1}^n{(x_i-\bar{x})^2}\left[\hat{b}^2-\frac{2\hat{b}\displaystyle \sum_{i=1}^n{(x_i-\bar{x})(y_i-\bar{y})}}{\displaystyle \sum_{i=1}^n{(x_i-\bar{x})^2}}\right] =n[a^−(yˉ−b^xˉ)]2+i=1∑n(yi−yˉ)2+i=1∑n(xi−xˉ)2⎣⎢⎢⎢⎢⎡b^2−i=1∑n(xi−xˉ)22b^i=1∑n(xi−xˉ)(yi−yˉ)⎦⎥⎥⎥⎥⎤
通过完全平方公式对最后一项配方:
= n [ a ^ − ( y ˉ − b ^ x ˉ ) ] 2 + ∑ i = 1 n ( y i − y ˉ ) 2 + ∑ i = 1 n ( x i − x ˉ ) 2 { b ^ 2 − 2 b ^ ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ∑ i = 1 n ( x i − x ˉ ) 2 + [ ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ∑ i = 1 n ( x i − x ˉ ) 2 ] 2 } − [ ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ] 2 ∑ i = 1 n ( x i − x ˉ ) 2 =\displaystyle n\left[\hat{a}-\left(\bar{y}-\hat{b}\bar{x}\right)\right]^2+ \sum_{i=1}^n{\left({y_i}-\bar{y}\right)^2}+\displaystyle \sum_{i=1}^n{(x_i-\bar{x})^2}\left\{\hat{b}^2-\frac{2\hat{b}\displaystyle \sum_{i=1}^n{(x_i-\bar{x})(y_i-\bar{y})}}{\displaystyle \sum_{i=1}^n{(x_i-\bar{x})^2}}+\left[\frac{\displaystyle \sum_{i=1}^n{(x_i-\bar{x})(y_i-\bar{y})}}{\displaystyle \sum_{i=1}^n{(x_i-\bar{x})^2}}\right]^2\right\}-\frac{\left[\displaystyle \sum_{i=1}^n{(x_i-\bar{x})(y_i-\bar{y})}\right]^2}{\displaystyle \sum_{i=1}^n{(x_i-\bar{x})^2}} =n[a^−(yˉ−b^xˉ)]2+i=1∑n(yi−yˉ)2+i=1∑n(xi−xˉ)2⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧b^2−i=1∑n(xi−xˉ)22b^i=1∑n(xi−xˉ)(yi−yˉ)+⎣⎢⎢⎢⎢⎡i=1∑n(xi−xˉ)2i=1∑n(xi−xˉ)(yi−yˉ)⎦⎥⎥⎥⎥⎤2⎭⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎫−i=1∑n(xi−xˉ)2[i=1∑n(xi−xˉ)(yi−yˉ)]2
整理得:
λ = n [ a ^ − ( y ˉ − b ^ x ˉ ) ] 2 + ∑ i = 1 n ( x i − x ˉ ) 2 [ b ^ − ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ∑ i = 1 n ( x i − x ˉ ) 2 ] 2 − [ ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ] 2 ∑ i = 1 n ( x i − x ˉ ) 2 + ∑ i = 1 n ( y i − y ˉ ) 2 \lambda =\displaystyle n\left[\hat{a}-\left(\bar{y}-\hat{b}\bar{x}\right)\right]^2+\displaystyle \sum_{i=1}^n{(x_i-\bar{x})^2}\left[\hat{b}-\frac{\displaystyle \sum_{i=1}^n{(x_i-\bar{x})(y_i-\bar{y})}}{\displaystyle \sum_{i=1}^n{(x_i-\bar{x})^2}}\right]^2-\frac{\left[\displaystyle \sum_{i=1}^n{(x_i-\bar{x})(y_i-\bar{y})}\right]^2}{\displaystyle \sum_{i=1}^n{(x_i-\bar{x})^2}}+ \sum_{i=1}^n{\left({y_i}-\bar{y}\right)^2} λ=n[a^−(yˉ−b^xˉ)]2+i=1∑n(xi−xˉ)2⎣⎢⎢⎢⎢⎡b^−i=1∑n(xi−xˉ)2i=1∑n(xi−xˉ)(yi−yˉ)⎦⎥⎥⎥⎥⎤2−i=1∑n(xi−xˉ)2[i=1∑n(xi−xˉ)(yi−yˉ)]2+i=1∑n(yi−yˉ)2因为现在我们是要求 a ^ , b ^ \hat{a},\hat{b} a^,b^所以不含有 a ^ , b ^ \hat{a},\hat{b} a^,b^的项全部看做常数即可,那么等式可以变形为:
λ = n [ a ^ − ( y ˉ − b ^ x ˉ ) ] 2 + t 1 [ b ^ − ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ∑ i = 1 n ( x i − x ˉ ) 2 ] 2 − t 2 + t 3 \lambda =\displaystyle n\left[\hat{a}-\left(\bar{y}-\hat{b}\bar{x}\right)\right]^2+\displaystyle t_1\left[\hat{b}-\frac{\displaystyle \sum_{i=1}^n{(x_i-\bar{x})(y_i-\bar{y})}}{\displaystyle \sum_{i=1}^n{(x_i-\bar{x})^2}}\right]^2-t_2+ t_3 λ=n[a^−(yˉ−b^xˉ)]2+t1⎣⎢⎢⎢⎢⎡b^−i=1∑n(xi−xˉ)2i=1∑n(xi−xˉ)(yi−yˉ)⎦⎥⎥⎥⎥⎤2−t2+t3
因为 λ \lambda λ 为误差系数,那么越趋近于0表明拟合程度越好,即我们需要求:
min ( λ ) \min(\lambda) min(λ)
然后根据方程可以知道,前两项都有平方,所以为非负数,所以前两项如果为0,那么 λ \lambda λ 的值就能达到最小.所以解方程即可得到:
{ b ^ = ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ∑ i = 1 n ( x i − x ˉ ) 2 = ∑ i = 1 n x i y i − n x ˉ y ˉ ∑ i = 1 n x i 2 − n x ˉ 2 a ^ = y ˉ − b ^ x ˉ \begin{cases} \displaystyle \hat{b}=\frac{\displaystyle \sum_{i=1}^n{(x_i-\bar{x})(y_i-\bar{y})}} {\displaystyle \sum_{i=1}^n{(x_i-\bar{x})^2}} =\frac{\displaystyle \sum_{i=1}^n{x_iy_i-n\bar{x}\bar{y}}} {\displaystyle \sum_{i=1}^n{x_i^2-n\bar{x}^2}} \\ \displaystyle \hat{a}=\bar{y}-\hat{b}\bar{x}\end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧b^=i=1∑n(xi−xˉ)2i=1∑n(xi−xˉ)(yi−yˉ)=i=1∑nxi2−nxˉ2i=1∑nxiyi−nxˉyˉa^=yˉ−b^xˉ
二、代码实现
- 有了公式再来使用代码实现就很简单了,这里我们先定义一个训练模型的函数,也就是求 a ^ , b ^ \hat{a},\hat{b} a^,b^的值:
import matplotlib.pyplot as plt
import numpy as np
def train_model(x_data,y_data):
x_size = np.size(x_data)
y_size = np.size(y_data)
mean_x = np.mean(x_data)
mean_y = np.mean(y_data)
# 求b帽
b = np.sum((x_data-mean_x)*(y_data-mean_y))/np.sum(np.power(x_data - mean_x,2))
# 求a帽
a = mean_y - b*mean_x
return a,b
- 随机生成数据:
# 从1到30 均匀的分成10份
x = np.linspace(1,30,10)
# 定义原数据,也就是真实的y值,为了模拟真实情况,所以加上随机值进行波动
y = x*10 + 5 + np.random.randint(-100,100,10)
- 训练模型并生成训练数据:
a,b = train_model(x,y)
y_ = b*x+a
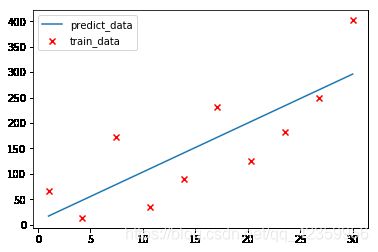
- 原数据和预测数据一起画在图中:
plt.scatter(x,y,c="r",marker="x",label="train_data")
plt.plot(x,y_,label="predict_data")
plt.legend()
后言:
哇…感觉这篇博客写了好久,主要是Tex语法还不是很熟悉,用起来有时候还需要取查,不过孰能生巧嘛,多用几次就熟练了,下一章将为大家讲述适用范围更广的线性回归方法,也是实际开发中会常用到的,今天的文章就到这里了,如果文章有错误,欢迎小伙伴指出,将不胜感激.错误也是一种成长,加油!