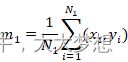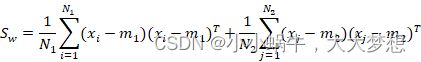LDA分类器
1.1 题目的主要研究内容
(1)介绍LDA分类器的原理和算法流程,并且熟练的运用LDA算法进行两类样本的分类运算;
(2)运用LDA算法对两类样本进行分类运算:
![]() :{(4,2),(2,4),(2,3),(3,6),(4,4)}
:{(4,2),(2,4),(2,3),(3,6),(4,4)}
![]() :{(9,10),(6,8),(9,5),(8,7),(10,8)}
:{(9,10),(6,8),(9,5),(8,7),(10,8)}
1.2 题目研究的工作基础或实验条件
(1)手动推演
通过手动推演实现算法流程,并且计算出分类结果;
(2)软件环境
通过MATLAB软件实现算法流程来验证手动推演结果,并且画出分类结果图。
1.3 设计思想
假设两类样本![]() :{(
:{(![]() ,
,![]() ),(
),(![]() ,
,![]() ),…,(
),…,(![]() ,
,![]() )},
)},![]() :{(
:{(![]() ,
,![]() ),(
),(![]() ,
,![]() ),…,(
),…,(![]() ,
,![]() )},其中i=
)},其中i=![]()
![]() ,j=
,j=![]()
![]() 。
。
(1)计算第一类样本均值向量![]()
![]() 和第二类样本均值
和第二类样本均值![]()
![]() 以及总样本均值m;
以及总样本均值m;
(2)计算散度矩阵,包括类内散度矩阵Sw和类间散度矩阵Sb;
![]()
(3)计算![]()
![]() 的所有特征向量和对应的特征值;
的所有特征向量和对应的特征值;
(4)选择最大特征值对应的特征向量W;
(5)对样本进行降维,得到对应的降维样本Y,其中Y=X·W。
1.4 流程图
图1 LDA算法流程图
1.5 主要程序代码(要求必须有注释)
定义FisherLDA函数代码:
function [W] = FisherLDA(w1,w2)
%W为最大特征值对应的特征向量
%w1 第一类样本
%w2 第二类样本
%第一步:计算样本均值向量
m1=mean(w1);%第一类样本均值
m2=mean(w2);%第二类样本均值
m=mean([w1;w2]);%总样本均值
%第二步:计算类内三都矩阵Sw
n1=size(w1,1);%计算第一类样本数量
n2=size(w2,1);%计算第二类样本数量
%求第一类样本的散度矩阵s1
s1=0;
for i=1:n1
s1=s1+(w1(i,:)-m1)'*(w1(i,:)-m1);
end
%求第二类样本的散度矩阵s2
s2=0;
for i=1:n2
s2=s2+(w2(i,:)-m2)'*(w2(i,:)-m2);
end
Sw=(n1*s1+n2*s2)/(n1+n2);
%第三步:计算类间散度矩阵Sb
Sb=(n1*(m-m1)'*(m-m1)+n2*(m-m2)'*(m-m2))/(n1+n2);
%第四步:求最大特征值和特征向量
%[V,D]=eig(inv(Sw)*Sb);%特征向量V,特征值D
A = repmat(0.1,[1,size(Sw,1)]);%repmat为创建所有元素值为0.1的1行size(Sw,1)列的矩阵
B = diag(A);%生成对角阵
[V,D]=eig(inv(Sw+B)*Sb);%求矩阵的全部特征值构成对角阵D,并求矩阵的特征向量构成V的列向量
[a,b]=max(max(D));%a为列最大值,b为列最大值的行号
W=V(:,b);%最大特征值对应的特征向量W
end
主函数LDA代码:
%给出两类样本
cls1_data=[4 2;2 4;2 3;3 6;4 4];
cls2_data=[9 10;6 8;9 5;8 7;10 8];
%样本投影前的二维坐标的点
plot(cls1_data(:,1),cls1_data(:,2),'.r');
hold on;
plot(cls2_data(:,1),cls2_data(:,2),'*b');
hold on;
%通过调用FisherLDA函数求出最大特征值对应的特征向量
W=FisherLDA(cls1_data,cls2_data);
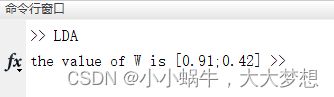
fprintf('the value of W is [%4.2f;%4.2f] ',W);
%画出样本投影直线
new1=cls1_data*W;
new2=cls2_data*W;
k=W(2)/W(1);
plot([0,12],[0,12*k],'-k');
axis([0 12 0 12]);
hold on;
%画出样本投影到直线上的点
for i=1:5
temp=cls1_data(i,:);
newx=(temp(1)+k*temp(2))/(k*k+1);
newy=k*newx;
plot(newx,newy,'*r');
end
for i=1:5
temp=cls2_data(i,:);
newx=(temp(1)+k*temp(2))/(k*k+1);
newy=k*newx;
plot(newx,newy,'ob');
end
1.6 运行结果及分析
通过图2的最佳向量W运行结果图可以看出MATLAB仿真出来的结果和手动推演的结果基本一致,不仅验证了手动推演的正确性,也验证了LDA的算法原理流程;通过图3的降维分类运行结果图可以看出是将二维平面里的坐标点降维到一维直线上,在一维直线上可以看出每一类样本点的类内距离最小,两类样本的类间距离最大,进一步验证了LDA算法的原理流程。
图2 最佳向量W运行结果图
图3 降维分类运行结果图