深蓝学院-视觉SLAM课程-第4讲作业(T5矩阵微分,T6手写高斯牛顿,T7批量MLE)
课程Github地址:https://github.com/wrk666/VSLAM-Course/tree/master
5. T5矩阵微分
5.1 实值行向量偏导
这块儿之前一直不太懂,趁着这个机会补一补。
看结论的话直接到5.5节,稍微理解一下的话再看看5.1和5.2,具体矩阵微分的引出在5.3。
行向量偏导和列向量偏导对应,对列向量偏导一般叫做梯度。

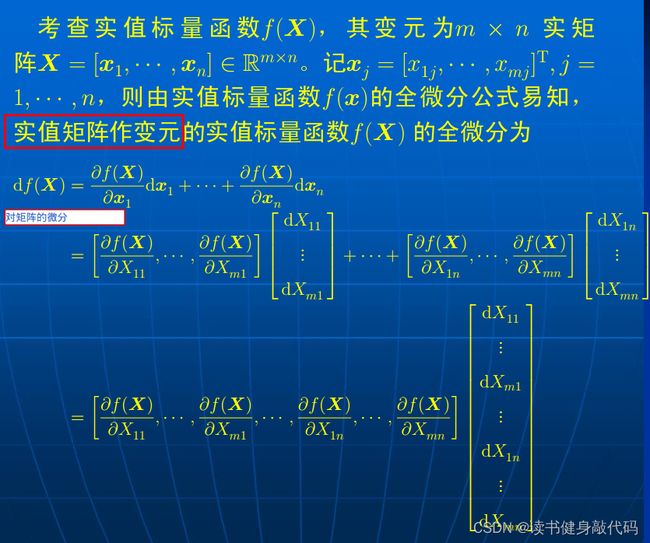
求 f ( X ) f(X) f(X)对 X X X的行向量偏导

vec()是矩阵的向量化函数,将矩阵变为列向量。则按照上面的步骤:
对于矩阵
[ X 11 ⋯ X 1 n ⋮ ⋱ ⋮ X m 1 ⋯ X m n ] \begin{bmatrix} X_{11} & \cdots &X_{1n} \\ \vdots & \ddots & \vdots \\ X_{m1} & \cdots & X_{mn} \end{bmatrix} ⎣⎢⎡X11⋮Xm1⋯⋱⋯X1n⋮Xmn⎦⎥⎤
先将X列向量化,
[ X 11 ⋮ X m 1 ⋮ X 1 n ⋮ X m n ] \begin{bmatrix} X_{11} \\ \vdots\\ X_{m1}\\ \vdots \\ X_{1n}\\ \vdots \\ X_{mn} \end{bmatrix} ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡X11⋮Xm1⋮X1n⋮Xmn⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
转置变为行向量,
[ X 11 ⋯ X m 1 ⋯ X 1 n ⋯ X m n ] = v e c T ( X ) \begin{bmatrix} X_{11} & \cdots & X_{m1} &\cdots & X_{1n} & \cdots X_{mn} \end{bmatrix}=vec^T(X) [X11⋯Xm1⋯X1n⋯Xmn]=vecT(X)
即可求得:

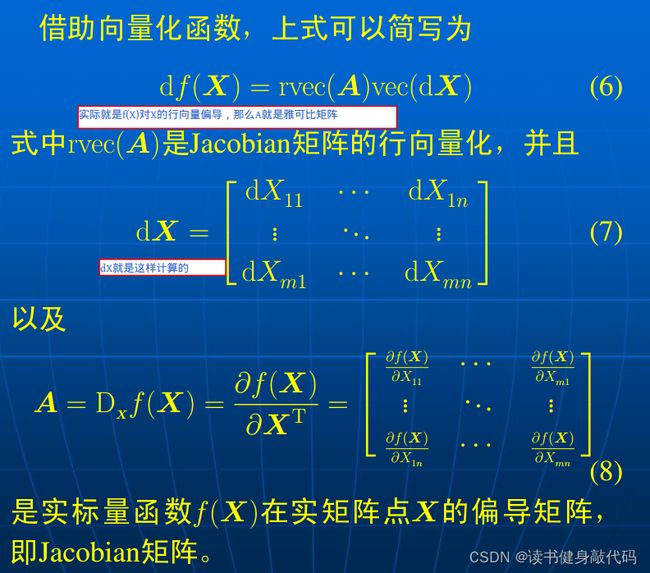
若直接以矩阵形式定义 f ( X ) f(X) f(X)在 X X X处的偏导,那就是求Jacobian矩阵(Jacobian矩阵也叫协(同)梯度矩阵,也有一些性质,目前用不到就暂不做介绍):

所以Jacobian矩阵就为:

行向量偏导与Jacobian有以下关系:
5.2 实列向量偏导
m × 1 m\times 1 m×1列向量偏导算子(即梯度算子):
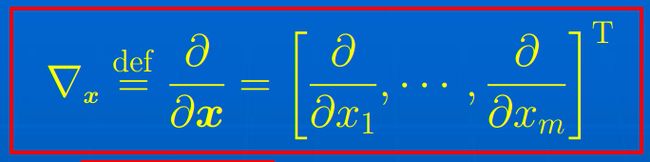
标量函数对列向量的偏导:

对矩阵的梯度算子(列向量偏导算子),将矩阵列向量化再逐个求导:

所以易得标量函数对矩阵X的的梯度矩阵的列向量形式为:

将上述结果矩阵化即得标量函数 f ( X ) f(X) f(X)的梯度矩阵,这是我们在优化中很常用的:
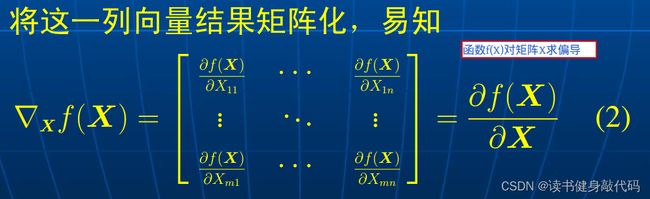
简单来说,对标量函数 f ( X ) f(X) f(X):
求其Jacobian矩阵:就是将 X X X转置,分别对 X i j X_{ij} Xij求偏导;
求梯度矩阵:直接对 X i j X_{ij} Xij求偏导
所以也可得:Jacobian矩阵是梯度矩阵的转置:


负梯度方向被称作变元 x \boldsymbol{x} x的的梯度流,记作:

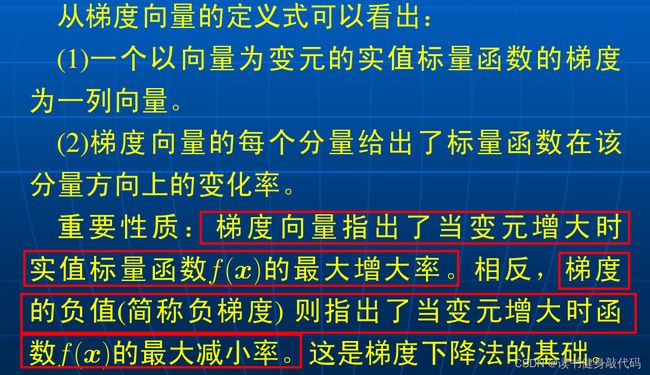
梯度向量指出了函数 f ( X ) f(X) f(X)的最大增大率,所以要实现梯度下降就得采用负梯度方向。
5.3 实值标量函数的Hessian矩阵



简单来说,求Hessian矩阵就是先求列向量偏导,再求行向量偏导。
5.4 矩阵微分


相对于实值函数 f ( ⋅ ) f(\cdot) f(⋅)还有向量函数 f ( ⋅ ) \boldsymbol{f}(\cdot) f(⋅),实矩阵函数 F ( ⋅ ) \boldsymbol{F}(\cdot) F(⋅),目前用不到,暂不做介绍。
5.4部分小结
实矩阵A(Jocabian矩阵)即为实值标量函数 f ( X ) f(X) f(X)相对于 X X X的一阶偏导矩阵。
且:
- Jocabian矩阵是唯一的
- Jocabian是梯度矩阵的转置,求 f ( X ) f(X) f(X)对于 X X X的梯度矩阵可由雅可比的转置直接给出(前面已经说过了)。
- 矩阵微分可以写成规范形式 d f ( X ) = t r ( A d X ) df(X)=tr(AdX) df(X)=tr(AdX)
5.5 实矩阵微分的计算


后面的可能不太常用,贴个结论:




介绍到这里,T5应该能很轻松拿下了。
其实还有很多东西需要再看,这里讲的主要是实值函数的矩阵/向量微分,第1问里面求的是向量对向量的微分,这里放几个博客:
矩阵求导术(上):主要是实值函数的矩阵微分。
矩阵求导术(下):主要是向量,矩阵函数的矩阵微分。
需要注意的是,向量对向量的微分的定义有些杂乱,不太清楚哪个是正确的
第1种定义:

第2种定义:
上面是列向量对列向量的导数,但是这篇博客中说的是列向量对行向量的微分以及行向量对列向量的微分

但是还是暂且接受下面这个结论来做题:
d f = ∂ f T ∂ x d x d\bm f=\frac{\partial{\bm{f}^T}}{\partial{\bm{x}}}d\bm x df=∂x∂fTdx
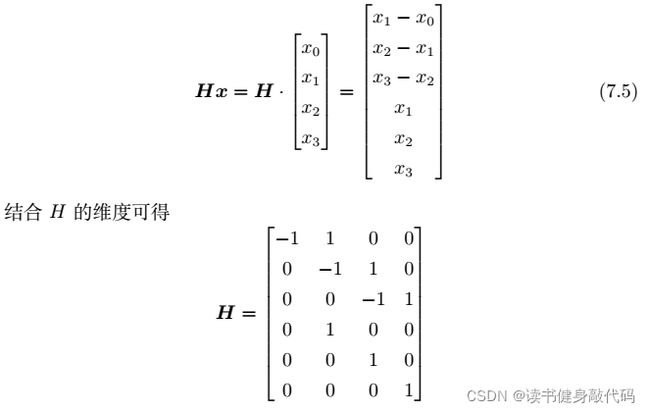
我的作业T5:
作业中求的应该是导数而不是微分,严格来写应该是
∂ A x ∂ x \frac{\partial{\bm{Ax}}}{\partial{\bm x}} ∂x∂Ax
说是对行向量求微分,(如果是对行向量的话,那上面的第二个)但是我搞不清楚了…
2022.3.7更新
其实实用的主要是向量对向量的求导,关键在于这个导数是怎么定义的,有地方定义成 ∂ 列 向 量 ∂ 列 向 量 \frac{\partial 列向量}{\partial 列向量} ∂列向量∂列向量,有地方定义成 ∂ 列 向 量 ∂ 行 向 量 \frac{\partial 列向量}{\partial 行向量} ∂行向量∂列向量,不管它怎么定义,我们求向量对向量的导数时,先抓住原则1:
![]()
先按照坟墓相同的维数分别对分母的各个元素求导
若是 ∂ 列 向 量 ∂ 列 向 量 \frac{\partial 列向量}{\partial 列向量} ∂列向量∂列向量的定义,则按原则2:

最终得到的求导结果就是:

如果是 ∂ 列 向 量 ∂ 行 向 量 \frac{\partial 列向量}{\partial 行向量} ∂行向量∂列向量的定义,那么原则2就是:按照分子展开
《14讲》的附录B就是这样定义的:

妈妈再也不用担心我的向量对向量求导了~



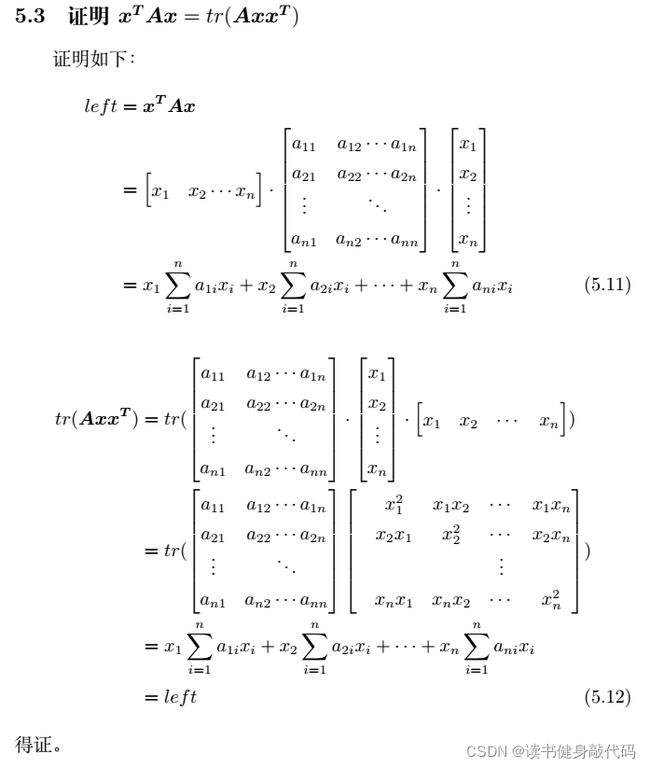
不知道有没有别的更简洁的方法,网上有别的答案,但是过程太短,我看不太懂,比如这篇里面的:

还有助教给的这个性质我也理解不了
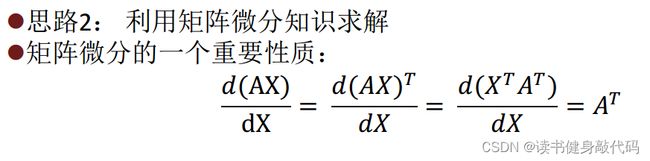
看了b站的一个视频,算是比较清楚地理解了矩阵微分(向量对向量求导)




6. T6 手写高斯牛顿的曲线拟合
for (int i = 0; i < N; i++) {
double xi = x_data[i], yi = y_data[i]; // 第i个 数 据 点
// start your code here
double error = yi - exp(ae * xi * xi + be * xi + ce); // 第i个数 据 点 的 计 算 误 差
Vector3d J; // 雅 可 比 矩 阵(是 一 个 列 向 量)
J[0] = -xi * xi * exp(ae * xi * xi + be * xi + ce); // de/da
J[1] = -xi * exp(ae * xi * xi + be * xi + ce); // de/db
J[2] = -exp(ae * xi * xi + be * xi + ce); // de/dc
//Hx=b
H += J * J.transpose (); // GN近 似 的H
b += -error * J;
// end your code here
cost += error * error;
}
// 求 解 线 性 方 程 Hx=b, 建 议 用ldlt
// start your code here
Vector3d dx = H.ldlt ().solve(b); //MatrixBase的Cholesky分 解 求 解 线 性 方 程 组
// end your code here
CMakeLists.txt:
cmake_minimum_required (VERSION 3.21)
project(T6)
set(CMAKE_CXX_STANDARD 11)
# OpenCV
find_package(OpenCV REQUIRED)
include_directories (${ OpenCV_INCLUDE_DIRS })
# Eigen
include_directories ("/usr/include/eigen3")
add_executable(gaussnewton gaussnewton.cpp)
target_link_libraries (gaussnewton ${OpenCV_LIBS })
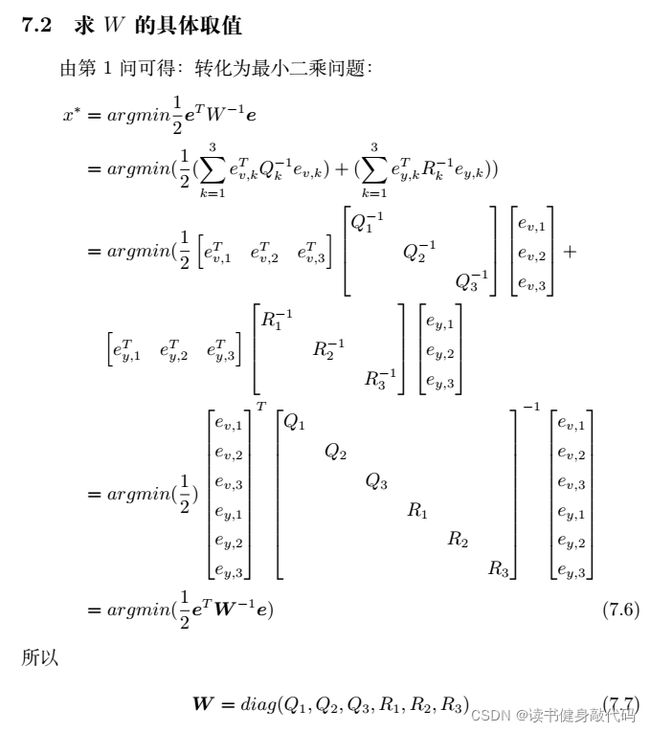
7. T7 批量最大似然估计
3.T3 鱼眼模型与去畸变
一些opencv的使用:
openCV 需要显示的图片太大超出了屏幕范围
Mat inputImg,outputImg;
cv::resize(inputImg,outputImg,cv::Size(1280,720)); //Size(1280,720)缩放后的图片尺寸
知道这里的point[2]是什么意思了,求的是原来的图像距离光心的距离r

上面这个不对,本来从像素到相机系就已经能进行去畸变了,去完畸变之后在转到像素系就行了,没必要求 P 0 P_0 P0的坐标。
鱼眼模型讲的好
助教的作业
剩下的可以看开头提到的Github,作业和程序都在里面。