Theta*: 连续环境下平滑的任意角度的路径规划

  此文翻译自这篇文章Theta*: Any-Angle PathPlanning for Smoother Trajectories in Continuous Environments，简单介绍了Theta*算法，这是一种基于A*的搜索算法。笔者翻译不妥的地方，还望谅解。

游戏AI的中心问题之一就是寻找一条看起来真实的短路径。路径规划通常可以分为两部分：简化一个连续的环境为一个离散化的图，并且通过搜索这个图来得到一条从给定的起始点到目标点的路径。视频游戏开发者（和机器人专家）为了解决这个离散问题开发了许多种方法：2D网格（正方形网格），六角形或三角形格子，3D网格（立方体网格），可视图，路点图，空间填充体（spacefilling volumes），导航网格，分层方法像是四叉树，概率道路图（PRMs）和快速探索随机树（RRTs）。

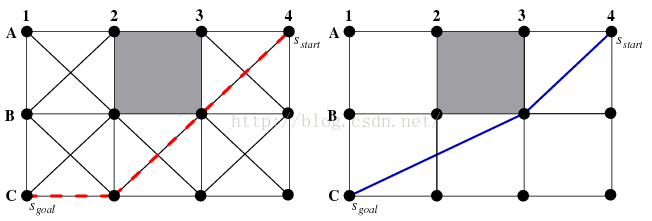
然而，由于A*的简单性和最优性，几乎总是会选择它作为搜索算法。这是因为A*能确保在图中找到一条最短的路径。A*的问题是虽然它能在图中找到一条最短的路径，但是这条路径并不是真实、连续的环境中的最短路径。A*通过图中的边来传播信息和约束路径的形成，图中的边会智能的约束路径的方向。插图1和2是一个连续环境分别离散化为2D网格和导航网格。2D网格和导航网格上的最短路径（插图1和2左侧）比连续环境中的最短路径（插图1和2右侧）更长，看上去更不真实。

插图1:2D网格中路径对比真实路径

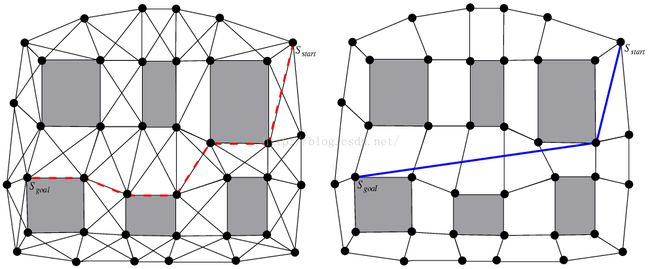
插图2： 导航网格中路径对比真实路径

  实际上A*的这种搜索到看上去不真实的较长路径的特性在视频游戏开发者社区中已经被很好的理解了。对于这个问题的一个通常的解决方式是施加一个后处理平滑技术来平滑所得到的路径。然而，选择这种后处理技术来找到一条看上去真实的路径是十分困难的。一个原因是A*搜索只保证找到最短路径的其中一条，然而一些路径可能会比其他路径更有效率的来执行平滑处理。比如A*能非常有效率的在2D网格中找到一条路径，它找到的路径是非常难以做平滑处理的且看起来非常不真实，因为它偏向于找对角线的路径。见插图3中红色的路径。

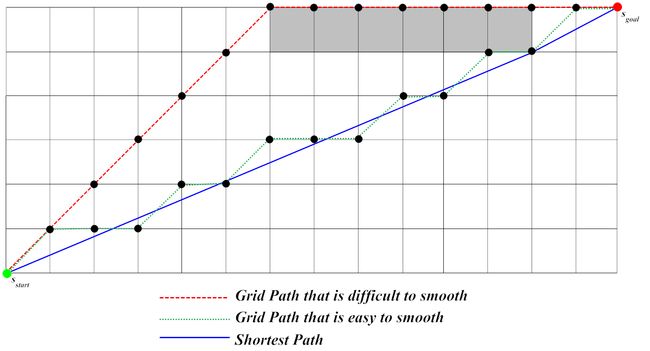
插图3：使用了平滑处理的A*寻路

A* 美学优化

  这曾是作者（Alex Nash）与Sven Koenig，KennyDaniel 和Ariel Felner一起写的一篇论文的主题。在论文里我们展示了一种新的搜索算法，称为Theta*。Theta*是A*的一种变体，它会沿着图的边传播信息，但不会使路径限制在图的边上（寻找“任意角度”的路径）。Theta*是易于理解和实现的，快速的，且能找到看起来真实的短路径。Theta*的伪代码只比A*的伪代码多几行且有相近的执行速度，但是找到的路径几乎等同于最短路径（Theta*不需要后处理）。

  简洁起见，这边文章将使用2D网格来描述连续环境，灰色的方块代表障碍不能通过，白色的方块则可以通过。另外，我们使用网格的角点作为顶点而不是网格的中心点。不过这两个假设对于Theta*算法来说都不是必须的。我们的目标是从开始点到目标点之间找到一条看起来真实的短路径，且不能穿过障碍。如插图1所示。Theta* 的动机是结合两个现有的路径规划技术的优良属性。

• 可视图：可视图包含起始顶点，目标顶点和所有障碍物的角点。当且仅当一个顶点能够通过视线“看”到另一个顶点时，它会通过一条直线与另一顶点相连。也就是说，两顶点之间的连线不能穿过阻塞的格子。在可视图上的最短路径也同样是连续环境上的最短路径。如插图1右侧所示。然而路径规划在非常大的可视图上有一些慢，因为边的数目是随格子的数目呈二次方增长的。

• 网格：路径规划在网格上比可视图执行的要快，因为边的数目与格子数目呈线性关系。然而，通过格子的边来生成路径是次优的且看起来不真实，因为路径被人为的约束了，如插图1（左侧）所示。

  在本文中我们假设每个格子都有8个相邻的格子，设定V表示网格顶点的集合，s_start是搜索的开始点，s_goal是目标点。c(s,s')是顶点s 和 s'的直线距离，lineofsight(s,s') 是真当且仅当s 和 s'能互相通过视线“看”到。nghbr_vis(s)是顶点s能够“看”到的邻接点。

A*算法

插图4：A*伪代码

  Theta*建立在A*算法之上，因此值得在此介绍一下。A*使用h(s) 来预估顶点间的距离（h-values）。A*会为每个顶点维护两个值：（1）g-value是从开始点到当前点s的最短路径的长度。（2）父节点在搜索结束时用来提取路径。路径的提取是通过目标点的父指针不断回溯到起始点得到的。A*同时会维护两个结构：（1）Open List是一个包含顶点以扩展优先级排序的表。（2）Closed List包含了那些已经搜索了的顶点。A*会更新g_value和顶点s到未展开的邻接点s’：通过计算从开始点到s的路径（g(s)）和从s到s’的直线距离（c(s,s')）来计算出一个长度g(s) + c(s,s')。如果新的路径比当前最短路径还要短的话，它会更新g-value和s’的父节点。

  这些通过A*找到的路径经常开起来像是被一个醉汉创建出来的。这不仅是因为这些路径比最短路径要长，而且这些路径是被人工约束在网格上的。处理这个问题的最常见的技术就是后处理那条通过A*得到的路径。一种方法是拉紧这些路径，就像他们围绕在障碍上的 “橡胶带”。后处理技术缩短了路径，但是感觉上是装饰品。A*只考虑约束在网格边上的路径，于是搜索不能做出更加合理的决定。由此产生了这样一个事实：路径的拓扑结构是由A*搜索来决定的，而搜索算法却不知道后处理处理后的路径。此外，正像我们在插图3中看到的，选择一个能够简单有效的后处理平滑算法可能会是非常困难的。在一些情况下，后处理根本不能减少路径的长度，且有可能比最短路径增长8%。我们因此开发了Theta*，它在搜索期间不再约束路径在格子的边上，于是能够做出更合理的决定。

Theta* 算法

插图5：Theta* 算法伪代码

  Theta*与A*关键的不同是Theta*允许一个顶点的父亲可以是任意顶点，而A*只允许顶点的父亲必须是邻接点。Main函数和UpdateVertex函数和插图4中的相同因此没有列出来。我们使用一致的函数h(s) =c(s,s_goal) 来计算直线距离。Theta*与A*基本是一致的，除了Theta*会通过考虑以下两种路径来更新顶点s未展开的邻接点的g-value：

• 路径 1：和A*要做的一样，Theta*考虑从开始点到顶点s[= g(s)]和从s到s’的直线距离[= c(s,s')],得到一个长度g(s) + c(s,s')。

• 路径2：为了实现任意角度的路径，Theta*也会考虑从开始点到s的父节点的距离parent(s) [= g(parent(s))]和从parent(s)到s’的直线距离[= c(parent(s),s')], 如果s’能够“看”到s的话；由此得到一个距离g(parent(s)) + c(parent(s),s')。如果s’能够“看”到parent(s)的话，由三角形不等式知道路径2一定比路径1要短。

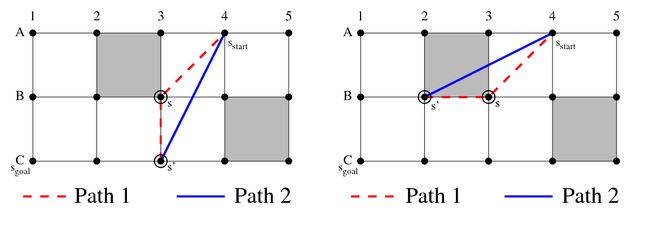
插图6：Theta*算法通过路径1和路径2分别更新点s

  如果任意一个路径比最短路径还要短，Theta*就会更新g-value和s’的父节点。比如：考虑插图6中从B3点（父节点A4）开始。B2是一个可扩展的邻接点，但是B2“看”不到A4，因此只能获得路径1（右图）。C3也是一个可扩展的邻接点，它可以“看”到A4，因此就可以得到路径2（左图）。

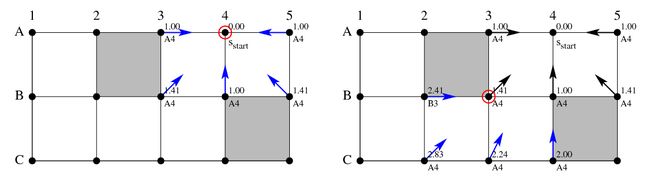
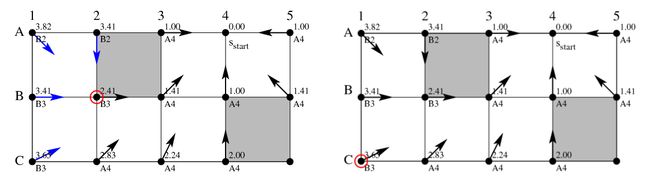
插图7：Theta*的追溯图

  插图7展示了Theta*一个完整的追溯图。每一个顶点用g-value 来作为标记，并且用一个箭头指向了它的父节点。空心圆指示出了当前正在扩展的顶点。开始点A4先开始扩展，之后是B3，B2和C1。

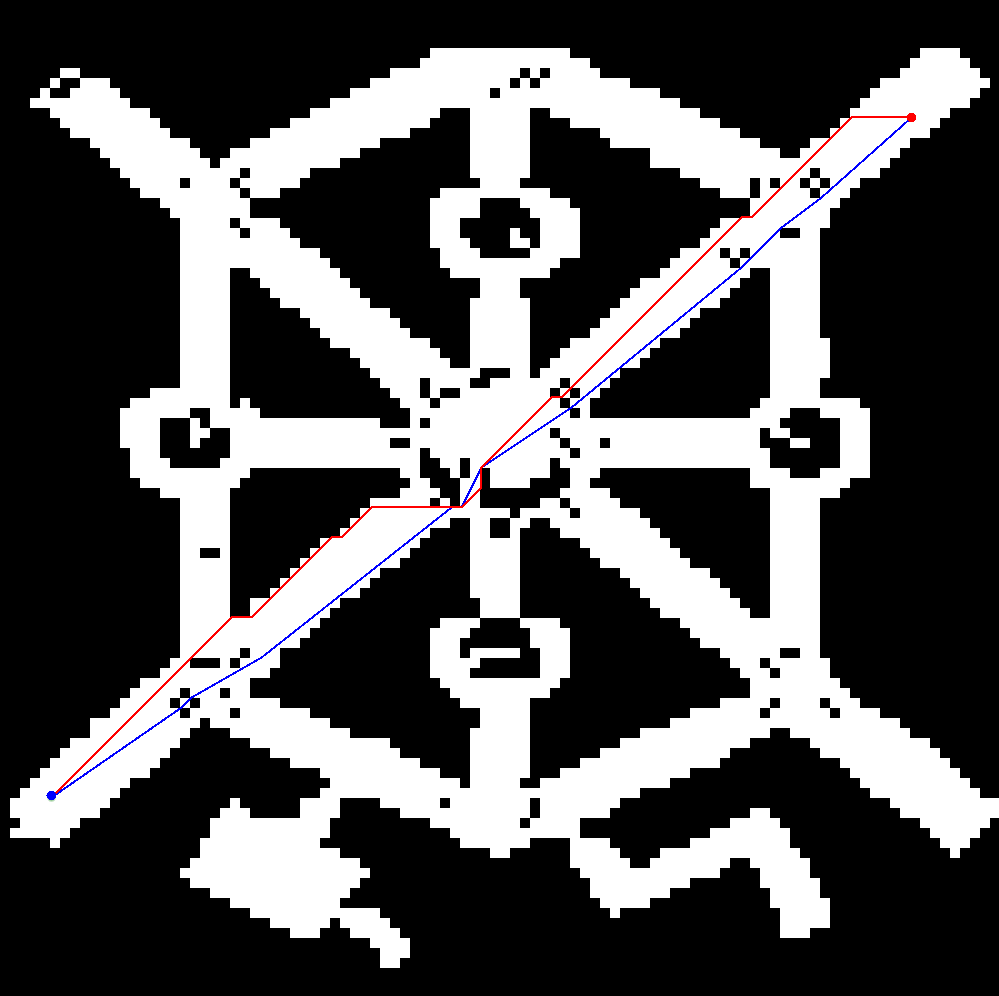
插图8：Theta*路径（蓝色）和A*路径（红色）

  插图8比较了Theta*和A*在Bioware的一个著名RPG博德之门中的一张地图上的搜索路径，这张地图被分为了100*100的正方形格子。Theta*算法的路径明显要更短看上去也更加真实。此外，A*算法的后处理平滑也不能把A*得到的路径处理成Theta*算法得到的路径，因为它们的拓扑结构是不一样的。

视线算法（Line-of-Sight）

  视线算法在正方形格子上可以执行的非常快，只需要比较整数值就可以了。因为执行视线算法很像是在两点之间绘制直线时，在光栅显示器上绘制点图形。所绘制的点对应于直线穿过的单元。于是，当且仅当所绘制的点没有落在阻塞的格子上两点能互相“看”到。这允许Theta*使用一个标准的整数运算了执行视线测试，而不使用浮点运算；如插图9所示，只有当对应的格子被阻塞时grid[x,y] 才是true. 方便起见，插图9中的伪代码在路径穿过阻塞格子会返回true。然而，Theta*不管路径是否能穿过阻塞的格子都是完整和正确的。

插图9：在正方形格子上的视线算法的伪代码

  当Theta*不保证能在连续环境中找到一条最短路径时，它会花费更大比例的时间找到最短路径。比如，插图10中，Theta*在连续环境中从那个大红点到每个蓝点都找到了最短路径。我们使用了一张游戏地图（博德之门）和一张随机地图来进行广泛的分析。

  我们发现平均来说Theta*找到的路径的长度与最短路径的比率在游戏地图上是1.007，在随机地图上是1.002.这明显比A*的比率1.04要好。Theta*只是比用octile distance heuristic 优化过的A*版本要慢一点。然而，当你结合后处理来看时，Theta*会更讨人喜欢。此外，在octileheuristic根本不存在的情况下，并不值得在导航网格上进行深度的优化。Theta*在可视图上比标准版A*的速度要快一个数量级。