寻路优化（二）——二维地图上theta*算法的设计探索

这篇文章是基于上一篇文章的研究上进行的，使得路径更加的平滑和自然，特此记录。有错误欢迎大家批评指正。如需转载请注明出处，http://www.cnblogs.com/Leonhard-/p/6866070.html，这是对作者最起码的尊重，谢谢大家。

本文结构如下：

一、Theta*算法、LazyTheta*算法背景介绍

二、Lazy Theta*算法介绍与实现简述

三、深入思考优化需求

　　1.网格中的阻挡判定

　　2.效果受A*算法影响

　　3.lazy theta* cost的限制

四、总结

 

一、Theta*算法、LazyTheta*算法背景介绍

　　在上一篇文章中，考虑的是用A*得到一条“最优”的算法，且尽可能的去防止玩家选择上的“抖动”。这里“最优”是基于一个前提，那就是必须沿着地图网格里的格子，一个格子一个格子的跳，像跳棋一样，也就是说，角色移动的角度只能是45的倍数。一条可能的移动路径如下：

　　这又出现了新问题，假设我们在现实生活中，走路会这么走吗？这让我们的寻路显得非常的僵硬。那最直接的方法就是直接从起点直接走向终点。那此时允许角色往任意角度移动的Theta*算法就派上了用场，而LazyTheta*在Theta*上做了一个性能优化，只对其中的一部分有必要处理的点进行处理。本文的目的就是讨论在二维网格地图上使用lazy theta*算法。

二、Lazy Theta*算法介绍与实现简述

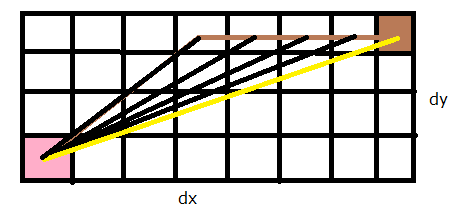
　　theta*算法和lazy theta*算法和A*算法大部分是一样的，只是theta*类算法比A*多了一个收缩父节点的操作，具体的theta*算法和lazy theta*算法的介绍可以参看这篇blog，这里就不再对重复的内容进行复制粘贴。这里简单的对实现思路进行一个简要的描述，如上图的路径，我们发现其实不需要记录A*算法结果的每一个点，只需要记录起点（s）和终点（d）还有拐角的点（p）三点即可，中间的值就可以通过插值得出。此时，我们把p把的父节点记录为s，而d的父节点记录为p。这样的话，在我们利用A*计算路径的过程之后，将A*算法得到的路径节点进行一一的检测，如果pcurrent、pcurrent->parent和pcurrent->parent->parent三点共线，那么我们直接把pcurrent->parent = pcurrent->parent->parent(A* with post-smoothed paths)。而theta算法，则在此基础上进一步优化，当我们把节点加入到open队列时，我们对该节点进行测试，如果pcurrent和pcurrent->parent->parent之间是否存在一条路径，则把pcurrent->parent = pcurrent->parent->parent并重新设置pcurrent的cost值，如果不存在就什么都不做。而Lazy theta*则是，把节点测试放到了节点从heap里弹出之后，减少了不必要的节点计算。下图为计算的过程。黑色斜线为中间计算结果，黄色线段为最后的结果，也就是说，在这幅图里，Lazy theta*的最终结果就是两个点，起点和终点。

三、深入思考优化需求

　　1.网格中的阻挡判定

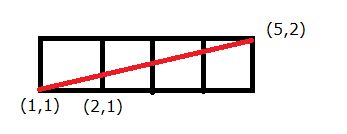
　　在之前的A*算法寻路中，要判定一个格子是否被占用，只需要对MapManager进行一次查询操作即可，但是现在的移动是任意角度的移动，这需要进一步考虑如何判定任意两个点之间是否存在一条路径。以dx>dy >0的情况为例子。

　　此时，当我们要判定当X=2时，在地图上是否能够通过时，此时我们需要判定（2,1）和（2,2）两个点的可达性，如果两点都可达，那么直线上的点在X=2时才可达。（也可以只判定一个点，但是这我们项目里，也可能会出现奇怪的现象，具体情况具体分析。而计算方法则可以通过给出直线方程的隐式方程来快速计算）

　　2.效果受A*算法影响

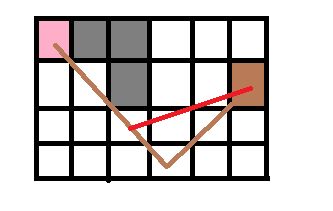
　　theta*算法可以优化A*的路径，但是如果A*算法部分做的不够好的话，theta*效果会大打折扣。下面以例子说明。

　　

　　如果A*的寻路结果如棕色线条时，我们期待的theta*优化结果如红色线条所示，但是，实际上拐角左边的线上的每一个点的parent都为s点，当进行拐角右边路线规划时，会计算该条线上每一点与source点的可达性，但是如图所示，此时的每一条线段是不可达的，所以，这种情况红色线条的优化不会发生。如果要让红色线条被优化的话，需要参照上一篇文章，修改A*的估值函数来实现。

　　3.lazy theta* cost的限制

　　如果优化线条成立，那么就得给予被优化的节点一个新的cost值。那么这个cost值有什么要求呢？这起码得符合三角形法则（斜边不能大于两边之和，也不能小于两边之差）。否则，在特殊的情况下会出现意想不到的问题，例如下图，按理说，走的10->20->30是最短的路径，但是因为优化路径的奇怪权值，会导致结果按100->200走。

四、总结

　　theta*算法可以让路径规划先得平滑自然，而且可以实现任意角度朝向的移动，还可以很方便的实现非网格地图的寻路计算。但是这相比A*算法也会增加额外的计算量，具体使用时，需要在效果和性能中间做一个权衡。

转载于:https://www.cnblogs.com/Leonhard-/p/6866070.html