NLP面试知识汇总
NLP面试知识汇总
- NLP面试知识汇总
-
-
- 1. ngram模型
- 2. word2vec
-
- Skip-gram
- CBOW
- word2vec训练trick
-
- 知识补充 *霍夫曼树*
- h i e r a r c h i c a l s o f t m a x hierarchical \ softmax hierarchical softmax 分层softmax
- n e g a t i v e s a m p l i n g negative \ sampling negative sampling 负采样
- 预训练模型问题
-
- Transformer模型结构
- BERT的输入和输出分别是什么?
- 不考虑多头的原因, s e l f a t t e n t i o n self \ attention self attention中词向量不乘 Q K V QKV QKV参数矩阵,会有什么问题?
- BERT的mask方式?
- 使用BERT预训练模型为什么最多只能输入512个词,最多只能两个句子合成一句?
- 为什么BERT在第一句前会加一个[CLS]标志?或者者说[CLS]位置的作用?
- S e l f A t t e n t i o n Self \ Attention Self Attention 的时间复杂度是怎么计算的?
- M u l t i h e a d S e l f A t t e n t i o n Multi\ head \ Self \ Attention Multi head Self Attention 的时间复杂度是怎么计算的?
-
NLP面试知识汇总
1. ngram模型
是一种统计语言模型。常用的有unigram(1-gram),bi-ngram,tri-gram。
理论依据:
ngram根据概率公式推导,依据条件概率和乘法公式,假设有两个词A和B,在A后出现B的概率为: p ( B ∣ A ) = p ( A B ) p ( A ) p(B|A)=\frac{p(AB)}{p(A)} p(B∣A)=p(A)p(AB)上述式子可解释为在 A A A同时出现时 A B AB AB同时出现的概率,有 p ( B ∣ A ) = c ( A B ) c ( A ) p(B|A)=\frac{c(AB)}{c(A)} p(B∣A)=c(A)c(AB)其中 c ( A B ) c(AB) c(AB)为文中 A B AB AB出现的次数, c ( A ) c(A) c(A)为 A A A出现的次数。
变为乘法公式有: p ( A B ) = p ( B ∣ A ) p ( A ) p(AB)=p(B|A)p(A) p(AB)=p(B∣A)p(A)从而得到ngram概率公式: p ( A 1 A 2 . . . A n ) = p ( A 1 ) p ( A 2 ∣ A 1 ) p ( A 3 ∣ A 2 A 1 ) . . . p ( A n ∣ A n − 1 . . . A 1 ) p(A_1A_2...A_n)=p(A_1)p(A_2|A_1)p(A_3|A_2A_1)...p(A_n|A_{n-1}...A_1) p(A1A2...An)=p(A1)p(A2∣A1)p(A3∣A2A1)...p(An∣An−1...A1)引入马尔科夫假设,即当前词的出现仅与之前几个词有关。即:
p ( A 1 , A 2 , . . . A n ) = p ( A i ∣ A i − m + 1 . . . A i − 1 ) p(A_1,A_2,...A_n)=p(A_i|A_{i-m+1}...A_{i-1}) p(A1,A2,...An)=p(Ai∣Ai−m+1...Ai−1)ngram模型中n的影响:
* n变大时:对下一个词的约束性信息增大,更大的辨别力,更稀疏,并且n-gram统计的的总数更多,为 [ w o r d − n u m V ] [word-num^V] [word−numV]个。
* n变小时:高频词次数更多,统计结果更可靠,更高的可靠性 ,但是约束信息更少。
n为特定值时,假设 ∣ V ∣ = 2 e 4 |V|=2e4 ∣V∣=2e4,统计次数为:
| n | ngram个数 |
|---|---|
| 1 | 4e8 |
| 2 | 8e12 |
| 3 | 1.6e17 |
2. word2vec
NLP中,最细粒度的是 词,词组成 句子,句子组成 段落、篇章、文档。而word2vec就是表征词的技术。
为什么要有Word2vec???
利用模型处理需要将文本转换成数值形式,即嵌入到一个数学空间,这种嵌入方式,就叫词嵌入 word embedding,而 Word2vec 就是词嵌入 word embedding 的一种,是一种无监督预训练方法。
Word2vec的两个学习方式 : Skip-gram和CBOW
word2vec到底怎样训练:
答:上述可知,处理文本需要将文本转换为可处理的数值形式,也就是利用词袋模型,转换为one-hot形式输送入模型进行训练,而在模型处理的过程中,会对one-hot进行一系列的线性或非线性变换,而在one-hot向量线性变换且降维操作中得到的产物,就是最终需要的词向量,也就是该层的权重。
Skip-gram
利用中心词预测上下文,一般为上下两个词。目标函数形式化为 最大化对数似然函数:
A i m f u n = ∑ w ∈ C l o g p ( C o n t e x t ( w ) ∣ w ) Aim \ fun=\sum_{w \in C}log \ p(Context(w)|w) Aim fun=w∈C∑log p(Context(w)∣w)
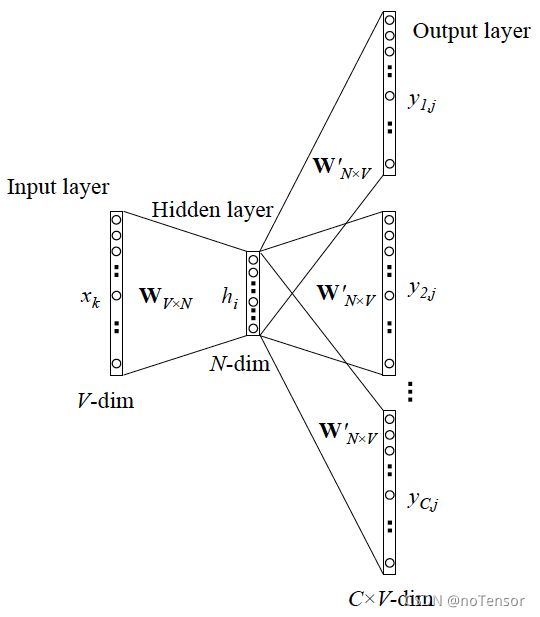
图中 W V ∗ N W_{V*N} WV∗N 即最终需要的整张词表,假设有 x i = [ 0 , 0 , 1 , . . . , 0 ] T ∈ R 1 e 5 x_i=[0,0,1,...,0]^T \in R^{1e5} xi=[0,0,1,...,0]T∈R1e5, 词表大小为 W 1 e 5 ∗ 768 W_{1e5*768} W1e5∗768,表示为 1 e 5 1e5 1e5个词,每个词768维向量。 x i ∗ W 1 e 5 ∗ 768 x_i*W_{1e5*768} xi∗W1e5∗768就会得到 W W W中第2行的向量,用以表征 x i x_i xi,维度从 1 e 5 1e5 1e5下降到768维。
CBOW
如图所示,训练方式为利用上下文词预测中心词。目标函数形式化为 最大化对数似然函数:
A i m f u n = ∑ w ∈ C l o g p ( w ∣ C o n t e x t ( w ) ) Aim \ fun=\sum_{w \in C}log \ p(w|Context(w)) Aim fun=w∈C∑log p(w∣Context(w))

word2vec训练trick
知识补充 霍夫曼树
原理来源:Huffman编码:一种用于无损数据压缩的熵编码(权编码)算法。
目标:出现概率高的符号使用较短的编码,出现概率低的符号则使用较长的编码。
数据结构:最优二叉树,表示一种带权路径长度 最短的二叉树。带权路径长度,指的就是叶子结点的权值乘以该结点到根结点的路径长度。
h i e r a r c h i c a l s o f t m a x hierarchical \ softmax hierarchical softmax 分层softmax
霍夫曼树在 word2vec 中的应用就是首先将词典中的每个词按照词频大小构建出一棵 Huffman 树,即用于后续的 s o f t m a x softmax softmax:
- 保证词频大处于浅层,词频低处于深层,每一个词都处于这棵 Huffman 树上的某个叶子节点。
- 将原本的一个 ∣ V ∣ |V| ∣V∣分类问题变成了 l o g 2 ∣ V ∣ log_2|V| log2∣V∣次的二分类问题。原先要计算 p ( w t c t ∣ ) p(w_tc_t|) p(wtct∣)的时候,普通 s o f t m a x softmax softmax要求词典中每个词的概率大小。在 H i e r a c h i c a l S o f t m a x Hierachical Softmax HierachicalSoftmax中,只需要把它变成在 H u f f m a n Huffman Huffman树中的路径预测问题就可以了,因为当前词 w c w_c wc在 H u f f m a n Huffman Huffman树中对应到一条路径,这条路径由这棵二叉树中从根节点开始,经过一系列中间的父节点,最终到达当前这个词的叶子节点而组成,那么在每一个父节点上,都对应的是一个二分类问题。
n e g a t i v e s a m p l i n g negative \ sampling negative sampling 负采样
普通 s o f t m a x softmax softmax的计算量太大是因为把词典中所有其他非目标词都当做负例,而负采样的思想是 每次按照一定概率随机采样一些词当做负例,从而就只需要计算这些负采样出来的负例,那么概率公式便相应变为: p ( w t ∣ c t ) = e x p ( e ′ ( w t ) T x ) ) ∑ i = 1 K e x p ′ ( w i ) T x x = ∑ i ∈ c e ( w i ) p(w_t|c_t)=\frac{exp(e^{'}(w_t)^Tx))}{\sum_{i=1}^{K}exp^{'}(w_i)^Tx} \quad x=\sum_{i \in c}e(w_i) p(wt∣ct)=∑i=1Kexp′(wi)Txexp(e′(wt)Tx))x=i∈c∑e(wi) 与普通 s o f t m a x softmax softmax 进行比较会发现,将原来的 ∣ V ∣ |V| ∣V∣分类问题变成了 K K K分类问题。
预训练模型问题
Transformer模型结构
和大多数seq2seq模型一样,transformer的结构也是由encoder和decoder组成。
- Encoder
每个Layer由两个sub-layer组成,分别是multi head self attention mechanism和fully connected feed-forward network。其中每层都加了residual connection和layer normalisation,因此可以将sub-layer的输出表示为: s u b _ l a y e r _ o u t p u t sub\_layer\_output sub_layer_output
BERT的输入和输出分别是什么?
输入: Token Embeddings + Segment Embeddings + Position Embeddings
Token Embeddings : 字向量,即每个字的表示
Segment Embeddings :表示当前字在第几个句子,对应Bert的NSP任务
Position Embeddings :位置向量表示
不考虑多头的原因, s e l f a t t e n t i o n self \ attention self attention中词向量不乘 Q K V QKV QKV参数矩阵,会有什么问题?
s e l f a t t e n t i o n self \ attention self attention 核心 是 用文本中的其它词来增强目标词的语义表示,从而更好的利用上下文的信息。
计算过程中一般会有 q = k = v q=k=v q=k=v,相等实际上指来自同一个基础向量。在实际计算时,因为乘了参数矩阵, q , k , v q,k,v q,k,v一般不相等。
那如果不乘,每个词对应的 q , k , v q,k,v q,k,v就是完全一样的。相同量级的情况下, q i q_i qi与 k i k_i ki点积的值会是最大的。在 s o f t m a x softmax softmax后的加权平均中, w i w_i wi词本身所占的比重将会是最大的,使得其他词的比重很少,无法有效利用上下文信息来增强当前词的语义表示。而乘以参数矩阵后,会使得每个词的 q , k , v q,k,v q,k,v都不一样,能很大程度上减轻上述的影响。
BERT的mask方式?
BERT的mask方式 :选择mask的 15%,并且其中有 80% 情况下使用mask掉这个词,10% 情况下采用一个任意词替换,剩余 10% 情况下保持原词汇不变。
为什么要mask 15%,而不是其它数值?为什么15%中还要分为80%mask,10%替换,10%保持?
原 论文 中表示是受到 完形填空 的启发。 而 p = 0.15 p=0.15 p=0.15的一个解释为:在一个大小为 1 / p = 100 / 15 ≈ 7 1/p=100/15\approx 7 1/p=100/15≈7的窗口中随机选一个词,类似CBOW中滑动窗口的中心词。
而分为 80%mask,10%替换,10%保持 的原因:
- 80%mask主要是保证模型能利用上下文预测该位置的词。
- 10%的概率用任意词替换去预测正确的词,相当于文本纠错任务,为BERT模型赋予了一定的文本纠错能力。
- 10%的概率保持不变,缓解了finetune时候与预训练时候输入不匹配的问题(预训练时候输入句子当中有mask,而finetune时候输入是完整无缺的句子,即为输入不匹配问题)。
缺点:
- 针对有两个及两个以上连续字组成的词,随机mask字割裂了连续字之间的相关性,使模型不太容易学习到词组的语义信息。
- 就是每批次数据中只有 15% 的标记被预测,这意味着模型可能需要更多的预训练步骤来收敛。
使用BERT预训练模型为什么最多只能输入512个词,最多只能两个句子合成一句?
可以更改 BERT config,设置更大 max_position_embeddings 和 type_vocab_size 值去满足自己的需求。
为什么BERT在第一句前会加一个[CLS]标志?或者者说[CLS]位置的作用?
加一个[CLS]标志,最后一层该位对应向量可以作为整句话的语义表示,从而 用于下游任务。无明显语义信息的符号 会更“公平”地融合文本中各个词的语义信息,从而更好的表示整句话的语义。
具体来说, s e l f a t t e n t i o n self \ attention self attention用文本中的其它词来增强自身所蕴含的语义信息,但是本身的语义会占主要部分,因此,[CLS]位本身没有语义,经过12层,得到的是融合所有词的加权平均信息,相比其他正常词,可以更好的表征句子语义。
S e l f A t t e n t i o n Self \ Attention Self Attention 的时间复杂度是怎么计算的?
S e l f A t t e n t i o n Self \ Attention Self Attention时间复杂度: O ( n 2 d ) O(n^2d) O(n2d),这里, n n n是序列的长度, d d d是 e m b e d d i n g embedding embedding的维度。
三个步骤:相似度计算, s o f t m a x softmax softmax和加权平均,时间复杂度分别是:
相似度计算为 Q ∈ R n ∗ d Q \in R^{n*d} Q∈Rn∗d和 K ∈ R d ∗ n K\in R^{d*n} K∈Rd∗n的两个矩阵相乘: ( n , d ) ∗ ( d ∗ n ) = O ( n 2 d ) (n,d)*(d*n)=O(n^2d) (n,d)∗(d∗n)=O(n2d) ,得到一个 ( n ∗ n ) (n*n) (n∗n)的矩阵
为何相似度计算复杂度为: O ( n 2 d ) ? O(n^2d)? O(n2d)?
- Q Q Q矩阵的每行会和 K K K矩阵的每列对应相乘相加,所以 r o w ∗ c o l row*col row∗col的复杂度为 d d d(维度)。
- Q Q Q和 K K K分别有 n n n行和 n n n列,执行 n ∗ n n*n n∗n次第一条的操作。
- 综上,时间复杂度为 O ( n 2 d ) O(n^2d) O(n2d)
s o f t m a x softmax softmax时间复杂度为: O ( n 2 ) O(n^2) O(n2)
加权平均可以看作大小为 ( n , n ) (n,n) (n,n)和 ( n , d ) (n,d) (n,d)的两个矩阵相乘,得到一个 ( n , d ) (n,d) (n,d)的矩阵,复杂度为 O ( n 2 d ) O(n^2d) O(n2d)
为何相似度计算复杂度为: O ( n 2 d ) ? O(n^2d)? O(n2d)? 与相似度计算复杂度有区别
- ( n , n ) (n,n) (n,n)相似度矩阵的每行会和 V V V矩阵的每列对应相乘相加,所以 r o w ∗ c o l row*col row∗col的复杂度为 n n n(行和列的维度)。
- ( n , n ) (n,n) (n,n)和 V V V分别有 n n n行和 d d d列,执行 n ∗ d n*d n∗d次第一条的操作。
- 综上,时间复杂度为 O ( n 2 d ) O(n^2d) O(n2d)
综上, S e l f A t t e n t i o n Self \ Attention Self Attention 的时间复杂度是 O ( n 2 d ) O(n^2d) O(n2d)。
M u l t i h e a d S e l f A t t e n t i o n Multi\ head \ Self \ Attention Multi head Self Attention 的时间复杂度是怎么计算的?
借鉴 S e l f A t t e n t i o n Self \ Attention Self Attention时间复杂度的计算,多头注意力在代码中是 t r a n s p o s e s a n d r e s h a p e s transposes \ and \ reshapes transposes and reshapes。
怎么理解?
代码中将 e m b e d d i n g embedding embedding的维度做了 t r a n s p o s e s transposes transposes,即 d i m = h e a d ∗ p e r _ h e a d _ d i m dim=head*per\_head\_dim dim=head∗per_head_dim,此时的维度为 [ b a t c h _ s i z e , t e x t _ l e n g t h , h e a d , p e r _ h e a d _ d i m ] [batch\_size,\ text\_length,\ \textcolor{red}{head},\ per\_head\_dim] [batch_size, text_length, head, per_head_dim], 然后 r e s h a p e s reshapes reshapes,即维度变为 [ b a t c h _ s i z e , h e a d , t e x t _ l e n g t h , p e r _ h e a d _ d i m ] [batch\_size,\ \textcolor{red}{head},\ text\_length,\ per\_head\_dim] [batch_size, head, text_length, per_head_dim]。
此时单样本的复杂度计算为:
- 相似度计算: Q ∈ R h e a d ∗ t e x t _ l e n g t h ∗ p e r _ h e a d _ d i m ∗ K T ∈ R h e a d ∗ p e r _ h e a d _ d i m ∗ t e x t _ l e n g t h = O ( h e a d ∗ t e x t _ l e n g t h 2 ∗ p e r _ h e a d _ d i m ) Q\in R^{head*text\_length*per\_head\_dim}*K^T\in R^{head*per\_head\_dim*text\_length}=O(head*text\_length^2*per\_head\_dim) Q∈Rhead∗text_length∗per_head_dim∗KT∈Rhead∗per_head_dim∗text_length=O(head∗text_length2∗per_head_dim),由于 d i m = h e a d ∗ p e r _ h e a d _ d i m dim=head*per\_head\_dim dim=head∗per_head_dim,所以复杂度为 O ( t e x t _ l e n g t h 2 d i m ) O(text\_length^2dim) O(text_length2dim),即 O ( n 2 d ) O(n^2d) O(n2d),后续 s o f t m a x softmax softmax计算与加权平均计算的复杂度同理。最后可得 M u l t i h e a d S e l f A t t e n t i o n Multi\ head \ Self \ Attention Multi head Self Attention复杂度与 S e l f A t t e n t i o n Self \ Attention Self Attention复杂度一样。
未完待续
