强化学习EasyRL学习笔记（五）、近端策略优化算法PPO

介绍

  Easy RL是由清华大学、北京大学以及中国科学院大学的三名硕士生编写的一门强化学习入门书籍，又称为“蘑菇书”Easy RL github地址。笔者主要从事博弈论、多智能体强化学习等方面的研究。最近在学习该本书，故将学习笔记和心得在这里记录下来，供大家观看交流。之后笔者也会继续更新有关多智能体和强化学习的内容，包括强化学习算法原理和代码实现、论文复现、强化学习竞赛等，对文章内容有任何问题或想一起学习强化学习相关内容可以邮件联系。（[email protected]）

五、近端策略优化PPO

1、同策略与异策略

  在第四章中介绍的PG、REINFORCE、A2C算法，都存在一个问题，就是数据采样效率比较低，每次策略更新之后，之前采样的数据都无法再使用。这是因为，策略更新前后，参数发生了改变，而轨迹的概率分布与参数密切相关，如果在参数更新之后还使用原来参数生成的轨迹，显然是非常不合理的。而只要是与环境互动的策略以及进行更新的策略属于同一个策略，都会存在这样的问题。

​ 如果考虑不使用同策略，而是用一个策略进行采样，而更新另一个策略，也会出现问题：
$$\nabla R_{\theta }=E_{{\tau }_k\sim {\pi }_{\theta }({\tau }^k)}\sum _{t=1}^n\nabla log{\pi }_{\theta }(a_t^k|s_t^k)R({\tau }^k)=E_{{\tau }_k\sim {\pi }_{\theta }({\tau }^k)}\nabla log{\pi }_{\theta }({\tau }^k)R({\tau }^k)$$
  在上面的更新过程中，假设采样的数据来自于分布${\pi }_{{\theta }^{\prime }}$,而更新时则对参数$\theta$进行更新(或者说要计算的是$E_{{\tau }_k\sim {\pi }_{\theta }({\tau }^k)}\nabla log{\pi }_{\theta }({\tau }^k)R({\tau }^k)$)，显然会出现问题。对此，可以首先假设以下情形：

  假设有一个分布p(x),在p(x)中采样出x，并计算f(x)的期望，显然其计算公式为：
$$E_{x\sim p(x)}[f(x)]=\int p(x)f(x)dx$$
  若此时并不知道p(x)，而只知道另一个概率分布q(x)，即只能够在q(x)中进行采样，那么可以用以下的方式来计算$E_{x\sim p(x)}[f(x)]$:
$$\begin{gathered} E_{x\sim p(x)}[f(x)]=\int p(x)f(x)dx=\int q(x)\frac{p(x)}{q(x)}f(x)dx \\ =E_{x\sim q(x)}[\frac{p(x)}{q(x)}f(x)] \end{gathered}$$
  经过上述推导可知，原式等价于在q(x)中采样x,去计算$\frac{p(x)}{q(x)}f(x)$的期望。因为策略梯度也可以改写为:
$$\begin{gathered} \nabla R_{\theta }=E_{{\tau }_k\sim {\pi }_{\theta }({\tau }^k)}\nabla log{\pi }_{\theta }({\tau }^k)R({\tau }^k) \\ =E_{{\tau }_k\sim {\pi }_{{\theta }^{\prime }}({\tau }^k)}\frac{p_{\theta }({\tau }^k)}{p_{{\theta }^{\prime }}({\tau }^k)}\nabla log{\pi }_{\theta }({\tau }^k)R({\tau }^k) \end{gathered}$$
  上述过程也称为重要性采样，$\frac{p_{\theta }({\tau }^k)}{p_{{\theta }^{\prime }}({\tau }^k)}$被称为重要性权重。借助上式，即可以实现通过策略${\pi }_{{\theta }^{\prime }}$采样，而更新策略${\pi }_{\theta }$，即用异策略的思想实现策略梯度，这也是TRPO以及PPO的重要思想。

  在实际做PG时，并不是给一条轨迹同样的奖赏，而是将每个状态-动作对分开计算，实际更新梯度的过程为：
$$E_{(s_t,a_t)\sim {\pi }_{\theta }}[A^{\theta }(s_t,a_t)\nabla log{\pi }_{\theta }(a_t^k|s_t^k)]$$
  其中，A表示奖赏减去基线，即优势函数。

  将上述过程该为异策略，即可得到：
$$\begin{gathered} E_{(s_t,a_t)\sim {\pi }_{{\theta }^{\prime }}}[\frac{p_{\theta }(s_t,a_t)}{p_{{\theta }^{\prime }}(s_t,a_t)}{A}^{{\theta }^{\prime }}(s_t,a_t)\nabla log{\pi }_{\theta }(a_t^k|s_t^k)] \\ =E_{(s_t,a_t)\sim {\pi }_{{\theta }^{\prime }}}[\frac{p_{\theta }(a_t|s_t)p_{\theta }(s_t)}{p_{{\theta }^{\prime }}(a_t|s_t)p_{{\theta }^{\prime }}(s_t)}{A}^{{\theta }^{\prime }}(s_t,a_t)\nabla log{\pi }_{\theta }(a_t^k|s_t^k)] \end{gathered}$$
  假设$p_{\theta }(s_t)=p_{{\theta }^{\prime }}(s_t)$,因为这个概率比较难算，因此得到：
$$E_{(s_t,a_t)\sim {\pi }_{{\theta }^{\prime }}}[\frac{p_{\theta }(a_t|s_t)}{p_{{\theta }^{\prime }}(a_t|s_t)}{A}^{{\theta }^{\prime }}(s_t,a_t)\nabla log{\pi }_{\theta }(a_t^k|s_t^k)]$$
  其中，$p_{\theta }(a_t|s_t)$很容易计算，可以再策略网络的输出中找到。上式是目标函数的梯度，此时可以反推出目标函数为：
$$J^{{\theta }^{\prime }}(\theta )=E_{(s_t,a_t)\sim {\pi }_{{\theta }^{\prime }}}[\frac{p_{\theta }(a_t|s_t)}{p_{{\theta }^{\prime }}(a_t|s_t)}{A}^{{\theta }^{\prime }}(s_t,a_t)]$$

2、TRPO/PPO算法

  经过上述分析发现，可以通过策略${\pi }_{{\theta }^{\prime }}$采样，而更新策略${\pi }_{\theta }$。但问题是，实际上策略${\pi }_{{\theta }^{\prime }}$和${\pi }_{\theta }$不能相差太多，尽管通过在两个分布中采样对不同的函数进行计算可以得到等价的期望，但实际上$Va{r}_{x\sim q(x)}[f(x)]和Va{r}_{x\sim q(x)}[\frac{p(x)}{q(x)}f(x)]$却可能因为两个分布的差异过大而导致差距很大，从而影响重要性采样的效果。

  对此，TRPO算法和PPO算法对${\pi }_{{\theta }^{\prime }}$和${\pi }_{\theta }$的差距做了约束，要求其差异要在一定范围内,也就是让$p_{\theta }(a_t|s_t)$和$p_{{\theta }^{\prime }}(a_t|s_t)$差异不要太大。TRPO和PPO的办法是让这两个概率分布的KL散度不要太大，在TRPO中，优化的目标函数为一个带约束的优化问题：
$$J_{TRPO}^{{\theta }^{\prime }}(\theta )=E_{(s_t,a_t)\sim {\pi }_{{\theta }^{\prime }}}[\frac{p_{\theta }(a_t|s_t)}{p_{{\theta }^{\prime }}(a_t|s_t)}{A}^{{\theta }^{\prime }}(s_t,a_t)],KL(\theta ,{\theta }^{\prime })<\delta$$
  PPO在TRPO的基础上进行了改动，首先将目标函数改为无约束的，即将KL散度作为正则化项加入目标函数中，有：
$$J_{PPO}^{{\theta }^{\prime }}(\theta )=E_{(s_t,a_t)\sim {\pi }_{{\theta }^{\prime }}}[\frac{p_{\theta }(a_t|s_t)}{p_{{\theta }^{\prime }}(a_t|s_t)}{A}^{{\theta }^{\prime }}(s_t,a_t)]-\beta KL(\theta ,{\theta }^{\prime })$$

KL散度：又称为相对熵，用于衡量两个概率分布之间的差异性。KL散度越小，表明两个分布的差距越小。
$$KL(P||Q)=\int P(x)log\frac{P(x)}{Q(x)}dx$$

  这里计算的KL散度是计算在$\theta$和${\theta }^{\prime }$下每个状态下输出的动作空间上概率分布的差异。

3、近端策略优化算法惩罚PPO-penalty

  PPO有两个重要的变种，分别是近端策略惩罚PP01和近端策略裁剪PPO2。PPO1算法基本就是基于上面的步骤，目标函数为：
$$J_{PPO1}^{{\theta }^k}(\theta )=\sum _{(s_t,a_t)\sim {\theta }^k}\frac{p_{\theta }(a_t|s_t)}{p_{{\theta }^k}(a_t|s_t)}{A}^{{\theta }^k}(s_t,a_t)-\beta KL(\theta ,{\theta }^k)$$
  PPO1的基本步骤为：

1. 借助策略${\theta }^k$与环境进行互动，采样得到大量状态-动作对。
2. 使用上面得到的数据，估计优势函数$$A^{{\theta }^k}(s_t,a_t)$$
3. 计算目标函数的梯度，进行多次参数更新(PS：这里参数完成一次更新之后，由于不用考虑采样的有更新的参数分布不同，所以可以继续进行更新，完成多次的参数更新。)，从而得到${\theta }^{k+1}$
4. 令${\theta }^k={\theta }^{k+1}$,重复进行上面的过程。

  PS：可以看出这里与环境互动的${\theta }^k$是过去的策略${\theta }_{old}$，因此PPO实际上是一种同策略算法。

  实际上，这里还有一个针对KL函数惩罚系数的自适应调整，即如果更新过后KL散度过大(可以设定一个阈值KLmax)，说明参数$\beta$过小，没有起到惩罚作用，因此应该增大$\beta$.反之，如果KL散度太小(也设定一个阈值KLmin)，说明$\beta$太大，惩罚太强，我们怕他只优化后面的一项，则应该减小$beta$.

4、近端策略优化算法裁剪PPO-clip

  PPO2算法没有控制KL散度，而是通过裁剪的方法控制$\frac{p_{\theta }(a_t|s_t)}{p_{{\theta }^k}(a_t|s_t)}$,其目标函数为：
$$\begin{gathered} J_{PPO2}^{{\theta }^k}(\theta )=\sum _{(s_t,a_t)\sim {\pi }_{{\theta }^k}}min\{\frac{p_{\theta }(a_t|s_t)}{p_{{\theta }^k}(a_t|s_t)}{A}^{{\theta }_k}(s_t,a_t), \\ clip(\frac{p_{\theta }(a_t|s_t)}{p_{{\theta }^k}(a_t|s_t)},1-ϵ,1+ϵ)A^{{\theta }_k}(s_t,a_t)\} \end{gathered}$$
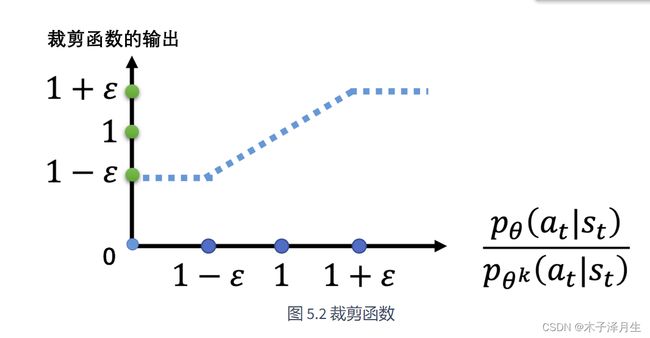
  其中，clip函数相当于完成了一个裁剪，若$\frac{p_{\theta }(a_t|s_t)}{p_{{\theta }^k}(a_t|s_t)}$小于$1-ϵ$,则返回$1-ϵ$；若$\frac{p_{\theta }(a_t|s_t)}{p_{{\theta }^k}(a_t|s_t)}$大于$1+ϵ$，则返回$1+ϵ$；否则返回$\frac{p_{\theta }(a_t|s_t)}{p_{{\theta }^k}(a_t|s_t)}$。剪裁函数的图像为：

  目标函数的效果为：

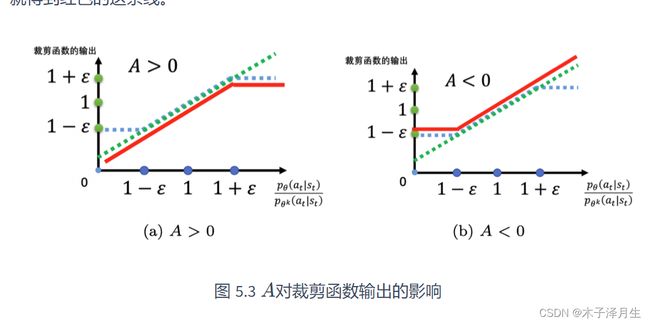
  图中画出了裁剪函数clip，以及函数$\frac{p_{\theta }(a_t|s_t)}{p_{{\theta }^k}(a_t|s_t)}$。当优势函数A大于0时，在最外层取了一个min，因此有了图a的红线。当A<0时，此时取min相当于对上述两个函数取最大，因此有了图b中的红线。

  对于上图，当优势函数大于0时，应该增大该状态-动作对出现的概率函数$p_{\theta }(a_t|s_t)$。当与此同时，也不能令其太大，当增大到比值$\frac{p_{\theta }(a_t|s_t)}{p_{{\theta }^k}(a_t|s_t)}$超过1+$ϵ$时，就不会再继续增加。同样，当A小于0，应该减少该概率函数，但最低减小到$\frac{p_{\theta }(a_t|s_t)}{p_{{\theta }^k}(a_t|s_t)}=1-ϵ$.

  PS: 对于这里取min作用的解释：如果只用clip函数，也就相当于两边都给封住，那当A>0时，在优化过程中，有可能在$1-ϵ$处收敛了(因为在这附近时，发现目标函数一直不变),但实际上我们希望得到更大的目标函数值。同样，当A<0时，有可能在1+$ϵ$处收敛了，由于A<0,因此此时得到的目标函数值是较小的。

  因此，min的作用就是，只封住一端。当A大于0时，我们希望分子变大，此时只约束这个比值不要太大，封顶即可，不用封底。而A小于0时，我们希望分子变小，此时只约束这个比值不要太小，封底即可，不用封顶。