泊松分布和指数分布
一、泊松分布
1.1 泊松分布的定义
日常生活中,大量事件是有固定频率的。
- 某医院平均每小时出生3个婴儿
- 某公司平均每10分钟接到1个电话
- 某超市平均每天销售4包xx牌奶粉
- 某网站平均每分钟有2次访问
它们的特点就是,我们可以预估这些事件的总数,但是没法知道具体的发生时间。已知平均每小时出生3个婴儿,请问下一个小时,会出生几个?
有可能一下子出生6个,也有可能一个都不出生。这是我们没法知道的。
泊松分布就是描述某段时间内,事件具体的发生概率。
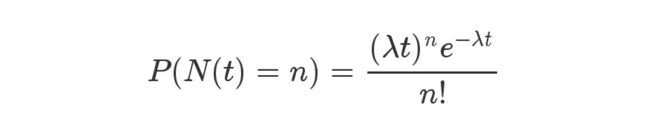
上面就是泊松分布的公式。等号的左边,P 表示概率,N表示某种函数关系,t 表示时间,n 表示数量,1小时内出生3个婴儿的概率,就表示为 P(N(1) = 3) 。等号的右边,λ 表示事件的频率。
接下来两个小时,一个婴儿都不出生的概率是0.25%,基本不可能发生。

接下来一个小时,至少出生两个婴儿的概率是80%。
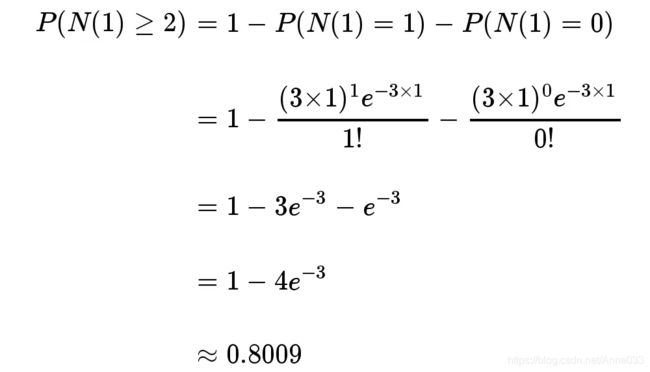
泊松分布的图形大概是下面的样子。

可以看到,在频率附近,事件的发生概率最高,然后向两边对称下降,即变得越大和越小都不太可能。每小时出生3个婴儿,这是最可能的结果,出生得越多或越少,就越不可能。
1.2 如何理解泊松分布?
1.2.1 甜在心馒头店
公司楼下有家馒头店:

每天早上六点到十点营业,生意挺好,就是发愁一个事情,应该准备多少个馒头才能既不浪费又能充分供应?

你“甜在心馒头店”又不是小米,搞什么饥饿营销啊?老板当然也知道这一点,就拿起纸笔来开始思考。
1.2.2 老板的思考
老板尝试把营业时间抽象为一根线段,把这段时间用T来表示:

把T均分为四个时间段:
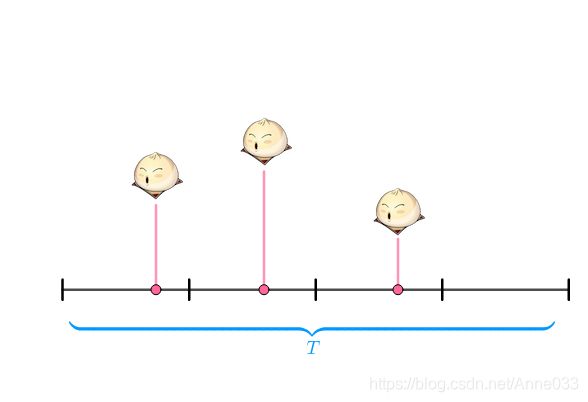
此时,在每一个时间段上,要不卖出了(一个)馒头,要不没有卖出:

在每个时间段,就有点像抛硬币,要不是正面(卖出),要不是反面(没有卖出)
T内那么卖出3个馒头的概率,就和抛了4次硬币(4个时间段),其中3次正面(卖出3个)的概率一样了。
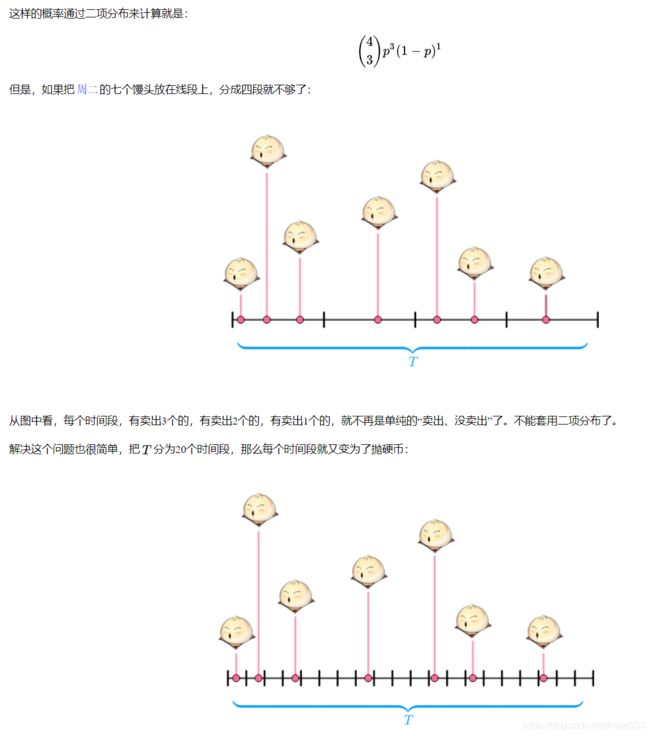

1.2.3 p的计算
“那么”,老板用笔敲了敲桌子,“只剩下一个问题,概率p怎么求?”

1.2.4 泊松分布
1.2.5 馒头店的问题的解决
老板依然蹙眉,不知道 μ \mu μ啊?
没关系,刚才不是计算了样本均值:
X ‾ = 5 \overline{X}=5 X=5
可以用它来近似:
X ‾ ≈ μ \overline{X}\approx\mu X≈μ
于是:
P ( X = k ) = 5 k k ! e − 5 P(X=k)=\frac{5^k}{k!}e^{-5} P(X=k)=k!5ke−5
画出概率质量函数的曲线就是:
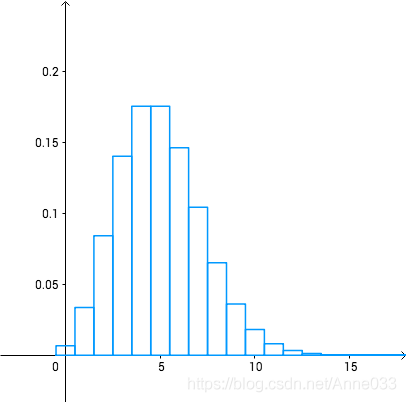
可以看到,如果每天准备8个馒头的话,那么足够卖的概率就是把前8个的概率加起来:

这样93%的情况够用,偶尔卖缺货也有助于品牌形象。
老板算出一脑门的汗,“那就这么定了!”
1.2.6 总结
这个故事告诉我们,要努力学习啊,要不以后馒头都没得卖。
生活中还有很多泊松分布。比如物理中的半衰期,我们只知道物质衰变一半的时间期望是多少,但是因为不确定性原理,我们没有办法知道具体哪个原子会在什么时候衰变?所以可以用泊松分布来计算。
1.3 泊松分布使用范围
Poisson分布主要用于描述在单位时间(空间)中稀有事件的发生数. 即需满足以下四个条件:
1、给定区域内的特定事件产生的次数,可以是根据时间,长度,面积来定义;
2、各段相等区域内的特定事件产生的概率是一样的;
3、各区域内,事件发生的概率是相互独立的;
4、当给定区域变得非常小时,两次以上事件发生的概率趋向于0。
例如:
1、放射性物质在单位时间内的放射次数;
2、在单位容积充分摇匀的水中的细菌数;
3、野外单位空间中的某种昆虫数等。
1.4 泊松分布的期望和方差
由泊松分布知 E [ N ( t ) − N ( t 0 ) ] = D [ N ( t ) − N ( t 0 ) ] = λ ( t − t 0 ) E[N(t) − N(t_0)] = D[N(t) − N(t_0)] = λ(t − t_0) E[N(t)−N(t0)]=D[N(t)−N(t0)]=λ(t−t0)
特别的,令 t 0 = 0 t_0=0 t0=0.由于假设 N ( 0 ) = 0 N(0)=0 N(0)=0,故可推知泊松过程的均值函数和方差函数分别为 E [ N ( t ) ] = λ t , D [ N ( t ) ] = λ t E[N(t)] = λt,D[N(t)] = λt E[N(t)]=λt,D[N(t)]=λt,
泊松过程的强度 λ \lambda λ(常数)等于单位长时间间隔内出现的质点数目的期望值。即对泊松分布有: E ( X ) = D ( X ) = λ E(X) = D(X) = \lambda E(X)=D(X)=λ
15. 泊松分布的特征
1、泊松分布是一种描述和分析稀有事件的概率分布。要观察到这类事件,样本含量 n n n必须很大。
2、 λ \lambda λ是泊松分布所依赖的唯一参数。 λ \lambda λ值愈小,分布愈偏倚,随着 λ \lambda λ的增大,分布趋于对称。
3、当 λ = 20 \lambda= 20 λ=20时,分布泊松接近于正态分布;当 λ = 50 \lambda= 50 λ=50时,可以认为泊松分布呈正态分布。在实际工作中,当时就可以用正态分布来近似地处理泊松分布的问题。
二、指数分布
2.1 指数分布的定义
指数分布是事件的时间间隔的概率。
下面这些都属于指数分布。
- 婴儿出生的时间间隔
- 来电的时间间隔
- 奶粉销售的时间间隔
- 网站访问的时间间隔
指数分布的公式可以从泊松分布推断出来。如果下一个婴儿要间隔时间 t ,就等同于 t 之内没有任何婴儿出生。

反过来,事件在时间 t 之内发生的概率,就是1减去上面的值。

接下来15分钟,会有婴儿出生的概率是52.76%。

接下来的15分钟到30分钟,会有婴儿出生的概率是24.92%。
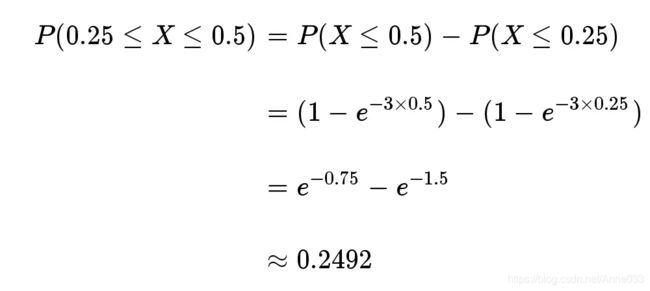
指数分布的图形大概是下面的样子。
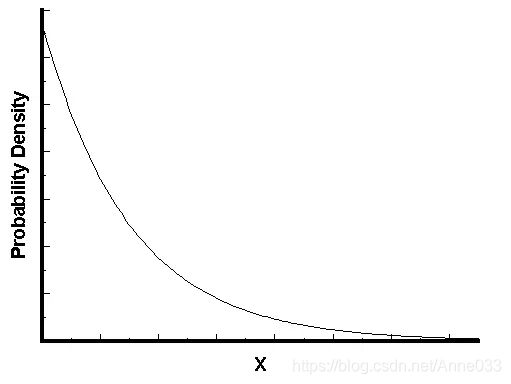
可以看到,随着间隔时间变长,事件的发生概率急剧下降,呈指数式衰减。想一想,如果每小时平均出生3个婴儿,上面已经算过了,下一个婴儿间隔2小时才出生的概率是0.25%,那么间隔3小时、间隔4小时的概率,是不是更接近于0?
指指数分布的概率密度为:

式中: x x x是给定的时间; λ \lambda λ为单位时间事件发生的次数; e = 2.71828 e=2.71828 e=2.71828。
2.2 指数分布的特征
指数分布具有以下特征:
(1)随机变量 X X X的取值范围是从0到无穷;
(2)极大值在 x = 0 x=0 x=0处,即 f ( x ) = λ f(x)=\lambda f(x)=λ;
(3)函数为右偏,且随着 x x x的增大,曲线稳步递减;
(4)随机变量的期望值和方差为 μ = 1 / λ , σ 2 = 1 / λ 2 \mu=1/\lambda,\sigma^2=1/\lambda^2 μ=1/λ,σ2=1/λ2。
通过对概率密度函数的积分,就可以得到相应的概率,其表达式有两种
P ( X ≥ x ) = e − λ x P(X\geq x)=e^{-\lambda x} P(X≥x)=e−λx
P ( X ≤ x ) = 1 - e − λ x P(X\leq x)=1-e^{-\lambda x} P(X≤x)=1-e−λx
例:某电视机生产厂生产的电视机平均10年出现大的故障,且故障发生的次数服从泊松分布。
问(1)该电视机使用15年后还没有出现大故障的比例;(2)如果厂家想提供大故障免费维修的质量担保,但不能超过全部产量的20%,试确定提供担保的年数。
解:
(1)设X为电视机出现大故障的时间。已知 μ = 10 \mu=10 μ=10年,则 λ = 1 / μ = 0.1 \lambda=1/\mu=0.1 λ=1/μ=0.1,于是, P ( X ≥ x ) = e − λ x = e − 0.1 ∗ 15 ≈ 0.223 P(X≥x)=e^{-λx}=e^{-0.1*15}≈0.223 P(X≥x)=e−λx=e−0.1∗15≈0.223。则15年后,没有出现大故障的电视机约占22.3%。
(2)问题要求比例不超过20%,这是求X的右侧概率面积,现在根据公式确定适当的X值。
从表中可以看到:担保2年时,出现大故障的比例是18.1%,不超过20%。担保3年时,出现大故障的比例为25.9%,已经超过20%。所以,厂家应以2年为担保期。
三、总结
一句话总结:泊松分布是单位时间内独立事件发生次数的概率分布,指数分布是独立事件的时间间隔的概率分布。
请注意是”独立事件”,泊松分布和指数分布的前提是,事件之间不能有关联,否则就不能运用上面的公式。
https://www.matongxue.com/madocs/858/
http://www.woshipm.com/pmd/163461.html
https://www.cnblogs.com/think-and-do/p/6483335.html



