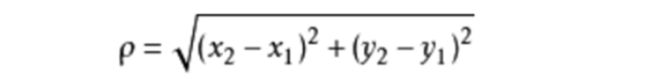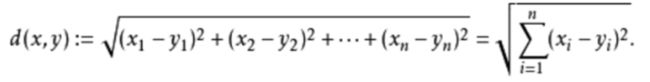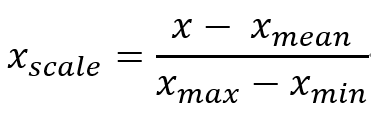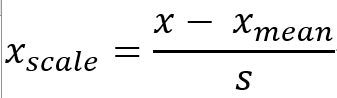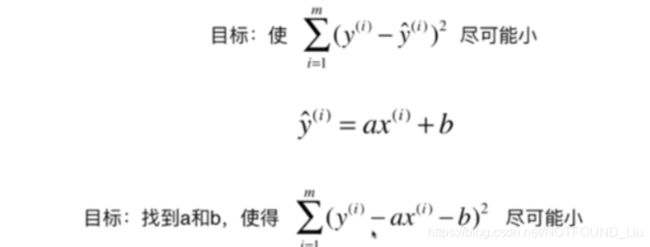软件技术部第一次机器学习培训
软件技术部第一次机器学习培训
学习方式
监督学习
在监督式学习下,输入数据被称为“训练数据”,每组训练数据有一个明确的标识或结果。在建立预测模型的时候,监督式学习建立一个学习过程,将预测结果与“训练数据”的实际结果进行比较,不断的调整预测模型,直到模型的预测结果达到一个预期的准确率。监督式学习的常见应用场景如分类问题和回归问题。
非监督学习
在非监督式学习中,数据并不被特别标识,学习模型是为了推断出数据的一些内在结构。常见的应用场景包括关联规则的学习以及聚类等。(例如K-means算法)
半监督学习
在半监督式学习方式下,输入数据部分被标识,部分没有被标识,这种学习模型可以用来进行预测,但是模型首先需要学习数据的内在结构以便合理的组织数据来进行预测。应用场景包括分类和回归,算法算法首先试图对未标识数据进行建模,在此基础上再对标识的数据进行预测。
强化学习
在强化学习方式下,输入数据作为对模型的反馈,不像监督模型那样,输入数据仅仅是作为一个检查模型对错的方式,在强化学习下,输入数据直接反馈到模型,模型必须对此立刻作出调整。(例如游戏AI)
监督学习解决的两类主要问题
分类问题
通过训练,使得计算机可以将新的输入进行判断并分到某个已经规定的类别,或者将一系列输入进行自分类
回归问题
我们需要回归一个结果。在实际的回归问题中,我们常常会有一个训练集来训练“参数”,在经过训练之后就可以利用这些已有参数进行计算。
KNN算法
KNN算法介绍
KNN(K-Nearest Neighbor)算法是机器学习算法中最基础、最简单的算法之一。它既能用于分类,也能用于回归。KNN通过测量不同特征值之间的距离来进行分类。
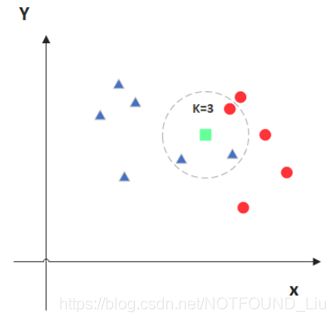
简化的KNN原理
KNN的原理就是当预测一个新的值x的时候,根据它距离最近的K个点是什么类别来判断x属于哪个类别。
距离的计算
通常KNN算法采用的是欧式距离。以二维空间为例,公式如下:
自己实现KNN代码
import numpy as np
import matplotlib.pyplot as plt
data_X = np.random.rand(10, 2)
data_y = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
print(data_X)
X_train = data_X
y_train = np.array(data_y)
#绘制散点图
plt.scatter(X_train[y_train==0, 0], X_train[y_train==0, 1], color='g')
plt.scatter(X_train[y_train==1, 0], X_train[y_train==1, 1], color='r')
plt.show()
#制造一个测试点
x = np.array([0.8, 0.7])
#将测试点也绘制进散点图
plt.scatter(X_train[y_train==0, 0], X_train[y_train==0, 1], color='g')
plt.scatter(X_train[y_train==1, 0], X_train[y_train==1, 1], color='r')
plt.scatter(x[0], x[1], color='b')
plt.show()
#计算距离
from math import sqrt
distances = []
for x_train in X_train:
d = sqrt(np.sum((x_train - x)**2))
distances.append(d)
#distances = [sqrt(np.sum((x_train-x)**2)) for x_train in X_train]与上面for循环等价的写法
nearest = np.argsort(distances)#计算距离
k = 6
nearest_k_y = [y_train[neighbor] for neighbor in nearest[:k]]
from collections import Counter
votes = Counter(nearest_k_y)
votes.most_common(1)#找出票数最多的一个元素
predict_y = votes.most_common(1)[0][0]
print(predict_y)
使用scikit-learn实现简单的KNN
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
data_X = np.random.rand(10, 2)
data_y = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
X_train = data_X
y_train = np.array(data_y)
x = np.array([0.7, 0.8]).reshape(1, -1)#不reshape会报错
KNN_classifier = KNeighborsClassifier(n_neighbors=6)#实例化一个分类器
KNN_classifier.fit(X_train, y_train)
y_predict = KNN_classifier.predict(x)
y_predict[0]
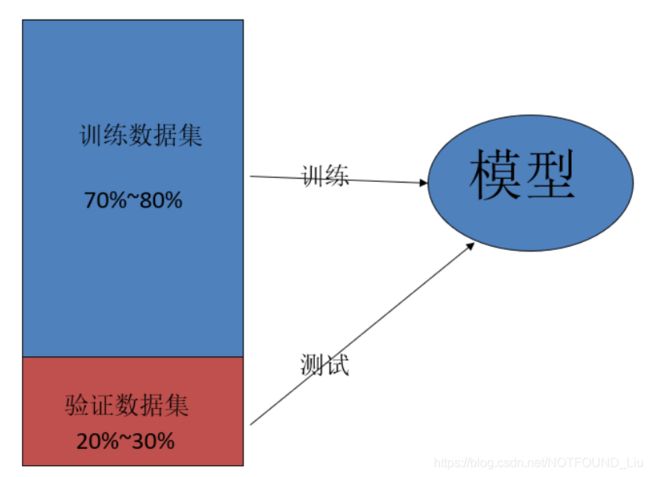
划分训练集和验证集
当模型在验证数据集上表现得不错时,这个模型才可能是可用的。
底层实现:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
iris = datasets.load_iris()#载入鸢尾花数据集
print(iris.keys())
X = iris.data
y = iris.target
#划分数据集
shuffled_indexes = np.random.permutation(len(X))#打乱索引
test_ratio = 0.2
test_size = int(len(X) * test_ratio)
test_indexes = shuffled_indexes[:test_size]
train_indexes = shuffled_indexes[test_size:]
X_train = X[train_indexes]
y_train = y[train_indexes]
X_test = X[test_indexes]
y_test = y[test_indexes]
print(X_train.shape)
print(y_train.shape)
print(X_test.shape)
print(y_test.shape)
使用sklearn实现:
from sklearn.model_selection import train_test_split
X_train1, X_test1, y_train1, y_test1 = train_test_split(X, y, test_size=0.2, random_state=5)
print(X_train1.shape)
print(y_train1.shape)
print(X_test1.shape)
print(y_test1.shape)
数据预处理
在机器学习领域中,不同评价指标往往具有不同的量纲和量纲单位,这样的情况会影响到数据分析的结果,为了消除指标之间的量纲影响,需要进行数据标准化处理,以解决数据指标之间的可比性。原始数据经过数据标准化处理后,各指标处于同一数量级,适合进行综合对比评价。
底层实现归一化:
import numpy as np
from sklearn import datasets
#最值归一化
x = np.random.randint(0, 100, 100)#生成100个数
x = (x - np.min(x)) / (np.max(x) - np.min(x))
print(x[:10])
#均值方差归一化
X2 = np.random.randint(0, 100, (50, 2))#生成50行2列的数组
X2 = np.array(X2, dtype=float)
print(X2[:10,:])
X2[:,0] = (X2[:,0] - np.mean(X2[:,0])) / np.std(X2[:,0])
X2[:,1] = (X2[:,1] - np.mean(X2[:,1])) / np.std(X2[:,1])
print(X2[:10, :])
使用sklearn进行预处理:
iris = datasets.load_iris()
X = iris.data
y = iris.target
print(x[:10, :])
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=666)
from sklearn.preprocessing import StandardScaler
standardScalar = StandardScaler()
standardScalar.fit(X_train)
standardScalar.mean_
standardScalar.scale_
print(X_train[:10,:])#此事并未对数据进行归一化
X_train = standardScalar.transform(X_train)#归一化处理
print(X_train[:10,:])
X_train = standardScalar.transform(X_train)
print(X_train[:10,:])
from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier(n_neighbors=3)
knn_clf.fit(X_train, y_train)
knn_clf.score(X_test_standard, y_test)
knn_clf.score(X_test, y_test)#错误示范,需要将归一化后测试集传入才行
补充:使用KNN解决回归问题
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
boston = datasets.load_boston()#导入波士顿房价数据集
X = boston.data
y = boston.target
X = X[y < 50.0]
y = y[y < 50.0]
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y)
from sklearn.preprocessing import StandardScaler
standardScaler = StandardScaler()
standardScaler.fit(X_train, y_train)
X_train_standard = standardScaler.transform(X_train)
X_test_standard = standardScaler.transform(X_test)
from sklearn.neighbors import KNeighborsRegressor
knn_reg = KNeighborsRegressor()
knn_reg.fit(X_train_standard, y_train)
knn_reg.score(X_test_standard, y_test)
简单的线性回归
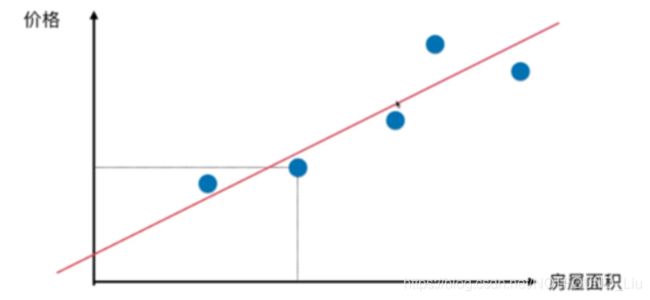
一元线性回归的原理
简而言之,我们通过拟合出一条直线以达到预测的效果。只需要找出一条直线,它预测出来的值与已知的值的误差尽可能小。
明确我们的目标
使用sklearn迅速实现简单的线性回归
import numpy as np
from sklearn import datasets
boston = datasets.load_boston()
X = boston.data
y = boston.target
X = X[y<50.0]
y = y[y<50.0]
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=6)
standardScalar = StandardScaler()
standardScalar.fit(X_train)
X_train = standardScalar.transform(X_train)
X_test_standard = standardScalar.transform(X_test)
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)
lin_reg.coef_
lin_reg.intercept_
lin_reg.score(X_test_standard, y_test)
ar.fit(X_train)
X_train = standardScalar.transform(X_train)
X_test_standard = standardScalar.transform(X_test)
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)
lin_reg.coef_
lin_reg.intercept_
lin_reg.score(X_test_standard, y_test)