机械手机基础（4）之机械手的两个雅可比矩阵（图像雅克比矩阵与机器人雅克比将矩阵）
机器人的两个雅可比矩阵
------前面的机械手基础（1）-（3），我们分别讲了机械手的相机模型，机械手的正逆运动学分析，机械手的基于位置和基于图像的视觉伺服控制方法。
------在这三个部分，我们似乎知道了的主要控制控制策略，那就是：
1）标定相机及机械手末端工具；
2）计算图像点到空间点坐标之间的转换关系；
3）估算机械手期望的末端位姿；
4）利用估算的期望末端位姿计算机械手各关节变量；
5）驱动机械手运动。
-------其中如何建立图像驱动机械关节运动这个环节还没打通，因此，在本节，我们将通过两个雅可比矩阵来说明其中的关系。
首先总结一下：
------机器人雅克比矩阵描述了机械手在真实三维空间中的末端工具的运动速度与关节角速度的线性转换关系，可以看作是从关节空间到机械手工作空间的比例关系。
------图像雅克比矩阵描述了摄像机图像特征空间速度与机械手末端工具运动速度的近似线性变换关系，从而建立了机械手末端操作空间与图像特征空间之间近似线性的非线性映射关系。
1. 机器人雅克比矩阵
------在向量微分学中，以一阶偏导数排列成的矩阵叫雅克比矩阵(Jacobian Matrix)。在数学中，微小的变化可以用微分变化来表达，所以雅克比矩阵的重要性在于它体现了一个可微分方程与给出点的最优线性逼近。
------假设 : f : R n → R m f:\mathbb{R}^{n}\rightarrow \mathbb{R}^{m} f:Rn→Rm是一个从n维欧氏空间映射到 m 维欧氏空间的线性的或者非线性函数。这个函数由m 个实函数组成： y 1 ( x 1 , . . . , x n ) , . . . , y m ( x 1 , . . . , x n ) y_{1}(x_{1},...,x_{n}),...,y_{m}(x_{1},...,x_{n}) y1(x1,...,xn),...,ym(x1,...,xn)，这些函数的偏导数可以组成一个 m × n m\times n m×n的矩阵，如下式所示。
-------------------------------------------------------------------------------(1)
------J 就是雅克比矩阵，它表从 R n \mathbb{R}^{n} Rn到 R m \mathbb{R}^{m} Rm的线性映射，其作用就是它表现了一个多变数的向量函数的最佳线性逼近。机器人雅克比矩阵描述了机械手在真实三维空间中的工作速度与关节角速度的线性转换关系。可以看作是从关节空间到机械手工作空间的比例关系，机械手的运动学方程为：
--------------------------------------------------------------------(2)
------上式代表机械手操作空间r与关节空间q 之间的位移关系，对上式求偏导就得到r 和q 之间的微分关系。
----------------------------------------------------------------------------(3)
------其中 r ˙ ∈ R m \dot{r}\in \mathbb{R}^{m} r˙∈Rm是末端在笛卡尔空间中的速度， q ˙ ∈ R n \dot{q}\in \mathbb{R}^{n} q˙∈Rn是关节速度， J r ( q ) ∈ R m × n J_{r}(q)\in \mathbb{R}^{m \times n} Jr(q)∈Rm×n是机器人雅克比矩阵，其具体表达形式如下。
------对端部位姿求微分，可写为 r ˙ = ( d x , d y , d z , w x , w x , w x ) \dot{r}=({d_{x},d_{y},d_{z},w_{x},w_{x},w_{x}}) r˙=(dx,dy,dz,wx,wx,wx) 。其中 d x , d y , d z d_{x},d_{y},d_{z} dx,dy,dz为末端沿xyz轴的微分运动， w x , w x , w x w_{x},w_{x},w_{x} wx,wx,wx为末端绕xyz的微分旋转。而我们也已经知道端部位姿矩阵关于关节变量的方程，例如
2. 图像雅可比矩阵
------关于图像雅可比矩阵，我们在第三讲的机器人基础（3）之基于图像的视觉伺服和基于位置的视觉伺服中讲到过。与机器人雅可比矩阵类似，图像雅可比矩阵是建立的是机械手末端瞬时速度与图像特征变化之间的关系（参见机器人基础（3）里面的公式3）。而机器人雅可比矩阵则建立的是操作空间速度与关节空间速度之间的线性变换。
------图像雅可比矩阵描述了摄像机图像特征空间速度与机械手末端操作空间运动微分 r ˙ \dot{r} r˙的近似线性变换关系，从而建立了机械手末端操作空间与图像特征空间之间近似线性的非线性映射关系，其微分关系如下式所示。
-------------------------------------------------------------(4)
------其中表示图像特征的变化速度， J i ( r ) ∈ R l × m J_{i}(r)\in \mathbb{R}^{l \times m} Ji(r)∈Rl×m 是图像雅克比矩阵，其表达式如下式 (5) 所示。
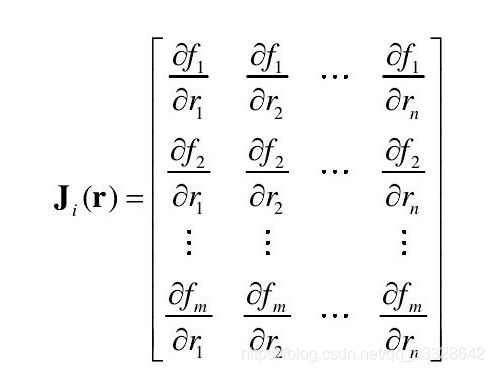------------------------------------------------------------------------------------------------------(5)
------图像雅克比矩阵描述了摄像机图像特征空间速度与机械手末端操作空间的近似线性变换关系，从而建立了机械手末端操作空间与图像特征空间之间近似线性的非线性映射关系，其微分关系如下式所示。
------------------------------------------------------------------(6)
通过式 (4)和式 (6)，可以得到图像特征空间与机械手关节空间之间线性变换关系，如下式 (7)所示。 J i ( q ) ∈ R l × n J_{i}(q)\in \mathbb{R}^{l \times n} Ji(q)∈Rl×n 建立了关节角变化到图像特征变化之间的近似线性化映射模型，同时也称为图像雅克比矩阵。
3. 他们是如何打通机械手的控制的
-----------------------------------------------------------------------------------------------(7)
------对于机械手视觉伺服，需要求解上面的逆过程，即知道图像特征变化，需要得到机械手末端工具的姿态变化；知道机械手末端工具的姿态变化，需要得到关节角变化，上述过程可以对机器人雅克比矩阵和图像雅克比矩阵求逆得到。
------摄像机小孔成像模型描述了如何把三维空间信息映射到二维图像平面，
------机械手运动学模型解决了机械手在笛卡尔空间中各关节之间的运动关系。
------机器人雅克比矩阵和图像雅克比矩阵模型分别描述了机械手关节空间与笛卡尔工作空间之间、笛卡尔工作空间与图像特征空间之间的微分线性变换关系。