ChatGPT通俗笔记:从GPT-N、RL之PPO算法到instructGPT、ChatGPT
前言
自从我那篇BERT通俗笔记一经发布,然后就不断改、不断找人寻求反馈、不断改,其中一位朋友倪老师(之前我司NLP高级班学员现课程助教老师之一)在谬赞BERT笔记无懈可击的同时,给我建议到,“后面估计可以尝试尝试在BERT的基础上,讲一讲prompt学习了”,然后我看了下prompt学习,一看果然牛..
再然后,当我还在各种改BERT笔记的时候,12月初突然出来了一个ChatGPT刷爆朋友圈,即便很多之前不接触AI的朋友也在问ChatGPT这种类似聊天机器人却远胜一般聊天机器人各种问题(上一次出现这种盛况的还是16年的AlphaGo)。
据我观察,大家问ChatGPT的问题千奇百怪,比如给他任意一段代码,要求它解释或添加对应的注释(这可不是单纯的翻译问题,需要有类似人的提炼、概括、总结能力),甚至有人让其根据要求排查代码bug,要知道此前debug想寻求帮助
- 要么问人(问熟人用社交软件,问陌生人则类似那种问答网站,持续问一般得付费,毕竟没人乐意持续免费答疑大量技术难题)
- 要么Google搜有没人遇到类似的问题(但别人遇到的问题很难与你的百分百一致)
所以ChatGPT就相当于你写代码或各类问题的私人顾问,而这个私人顾问能瞬间、精准理解你的意图,不会让你像用以前那种聊天机器人经常觉得智障甚至对牛弹琴,加之其背后依托的是人类级百科全书式的资料库,所以有人惊呼:ChatGPT会不会替代Google这类搜索引擎。
虽然大部分技术者对待ChatGPT还是比较冷静的,毕竟它给的答案不像权威技术专家那样具备足够的公信力,也不像Google给出来源从而不能比较好的验证其正确程度(注意我这里的措辞:“不能比较好的”、“正确程度”,^_^),但最近遇到的几件事改变了我的一些看法
- 这两天我刷到一条新闻:微软欲用 ChatGPT 扶必应“上位”,对抗 Google,导致即便很多技术从业者也不一定淡定了,当然,依然会有不少人始终淡定如一
- ChatGPT直接让其所在的公司OpenAI估值翻倍,而我司七月在线的最新一期NLP大课,NLP11也加入了ChatGPT的原理解析
- 因为ChatGPT太火,技术朋友经常会转发一些解释ChatGPT原理的资料,目前看到的资料里,先不说英文原始论文,中文资料里,现在各方面的知识、书籍、课程、资料很多,但真正能让人一看就懂的非常非常少
- 当少数文章具备比较好的可读性之后,你又会发现一旦涉及算法细节就千篇一律的泛泛而谈,如果不是泛泛而谈的,则更多堆砌概念和公式,总之中文资料里,可能因为instructGPT/ChatGPT刚出来不久的缘故,兼顾可读性和细节性的文章少的可怜
本篇ChatGPT笔记会全力做到,通俗易懂且循序渐进(另,本文配图均来自文末的参考文献,可以认为是针对文末参考文献的学习笔记)
- 一方面,对于想了解ChatGPT背后原理和如何发展而来的,逐一阐述从GPT/GPT2/GPT3到强化学习、PPO算法,最后再到instructGPT、ChatGPT、SeqGAN
且本文之前,99%的文章都不会把PPO算法从头推到尾,本文会把PPO从零推到尾,按照“RL-策略梯度-重要性采样(重要性权重)-TRPO(增加KL散度约束和信任区域)-PPO(解决TRPO计算量大的问题)”的顺序逐步介绍每一步推导(此部分内容核心参考自Easy RL教程,但为让初学者更好懂,补充了大量的解释说明,且倪老师帮拆解了部分公式) - 二方面,为彻底照顾初学者,本文会解释/说明清楚每一个公式甚至符号,包括推导过程中不省任何一个必要的中间推导步骤,以及必要的背景知识,十步推导绝不略成三步
本笔记从1.6日开始写(1.15日完成初稿,之后反复修改,春节期间基本成型,预计1月底完全成型,届时质量将是1.15日初稿的1.5-2倍),ChatGPT之后,再下一篇笔记应该是强化学习极简入门了。
第一部分 从GPT/GPT2到GPT3:微调到prompt学习的过渡
1.1 GPT:基于Transformer Decoder预训练 + 微调/Finetune
在上一篇BERT笔记中,我们已经了解到:GPT是“Generative Pre-Training”的简称,从名字看其含义是指的生成式的预训练。
GPT也采用两阶段过程,第一个阶段是利用语言模型进行预训练,第二阶段通过Fine-tuning的模式解决下游任务。
下图展示了GPT的预训练过程,其实和ELMO是类似的,主要不同在于两点:
- 首先,特征抽取器不是用的LSTM,而是用的Transformer,毕竟它的特征抽取能力要强于LSTM,这个选择很明显是很明智的;
- 其次,GPT的预训练虽然仍然是以语言模型作为目标任务,但是采用的是单向的语言模型
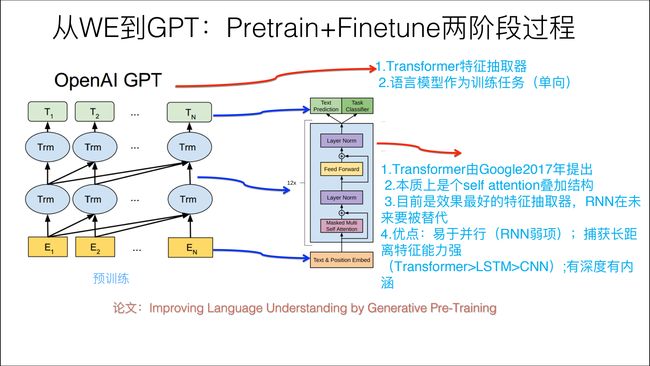
有两点值得提一下
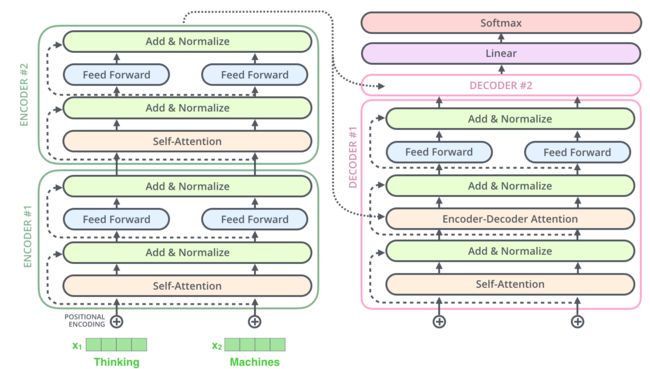
- 作为侧重生成式任务的GPT选择了Transformer Decoder部分作为核心架构(Decoder具备文本生成能力,故GPT在Transformer Decoder的基础上搭建语言模型Transformer Block:前馈神经网络feed forward + 自注意力机制self attention + 求和与归一化的前置LN层 + 残差)
- 关于Transformer 原理细节可以参看上一篇笔记BERT笔记(介绍的很细致),至于GPT的代码实现,网上有不少资料可以参看,比如GitHub
1.2 GPT2:舍弃微调,直接干zero-short learning
很多同学一看到DL,便会想到大数据,而数据量一大,还用CPU处理的话很可能训练一个小任务都得半天,而如果用GPU跑,可能一两分钟就出来了。于此,在深度学习大火的那几年,特别是AlphaGo出来的16年起,我司七月在线便分别为VIP、AI系统大课、在职提升大课、求职/论文/申博/留学1V1辅导提供GPU云平台进行实战训练。
然很多情况下,高质量数据的获取是比较困难的,比如医疗数据,那怎么办呢?既然暂时改变不了高质量数据匮乏的现状,那就改变模型! 如此,让模型能从少量样本中学习规律并具备推理能力便显得至关重要了。
最终,针对小样本/零样本的N-shotLearning应运而生,分为如下三种
- Zero-shot Learning (零样本学习),是指在没有任何训练样本进行微调训练的情况下,让预训练语言模型完成特定任务
- One shot Learning (单样本学习),顾名思义,是指在一个训练样本进行微调训练的情况下,预训练语言模型完成特定任务
- Few-shot Learning (少样本或小样本学习),类似的,是指在只有少量样本进行微调训练的情况下,预训练语言模型完成特定任务
而GPT-2不再使用二阶段训练模式(预训练+微调),而是彻底放弃了微调阶段,仅通过大规模多领域的数据预训练,让模型在Zero-shot Learming的设置下自己学会解决多任务的问题,而且效果还不错(虽然GPT2通过Zero-shot Learming在有些任务的表现上尚且还不如SOTA模型,但基本超越了一些简单模型,说明潜力巨大),你说神不神奇?
而GPT2在GPT1的基础上规模更大、模型更复杂。至于小样本学习的具体应用可以看下参考文献6。
1.3 GPT3:开启NLP新范式prompt从而实现小样本学习
GPT3简单来说,就是规模大、有钱多金、效果出奇好,具体而言,它的参数规模达到了1750亿,并且使用45TB数据进行训练,其预训练任务就是“句子接龙”,给定前文持续预测下一个字,而且只要有少量的文本数据就能作为模型的训练数据。
总之,只需将自然语言的提示信息(prompt)和任务示例(demonstration)作为上下文输入给GPT-3,它就可以在零样本或小样本的情况下执行任何NLP任务,包括所谓的完形填空任务,比如举个例子
比如,假如我要判断“我喜欢这个电影" 这句话的情感(“正面" 或者 "负面"),原有的任务形式是把他看成一个分类问题
输入:我喜欢这个电影
输出:“正面" 或者 "负面"
而如果用Prompt Learning去解决的话,任务可以变成“完形填空",
输入:我喜欢这个电影,整体上来看,这是一个 __ 的电影
输出:“有趣的" 或者 "无聊的"
言外之意即是,即便是面对完形填空似的任务,也能很好的解决
正因为GPT3首次把模型的规模带到了千亿级别,开辟了大模型赛道,其次也为NLP带来了一种新的范式prompt,prompt为GPT3带来了0样本、单样本、小样本的学习能力。而且更为关键的是,在小样本的情况下,其性能表现一度超越SOTA模型。
可想而知,prompt learning在GPT3中起到了一种极其关键的作用。所谓Prompt就是提示的意思。
例如我们有人忘记了某个事情,我们给予特定的提示,他就可以想起来,例如我们说:白日依山尽,大家自然而然地会想起来下一句诗:黄河入海流。
亦或者,搜索引擎,可以根据我们的输入,进行输出的提示:
那么在NLP中 Prompt 代表的是什么呢? prompt 就是给预训练语言模型的一个线索/提示,帮助它可以更好的理解人类的问题,这一创举揭开了GPT3在对话生成领域火力全开的序幕。
更多细节参见参考文献7。
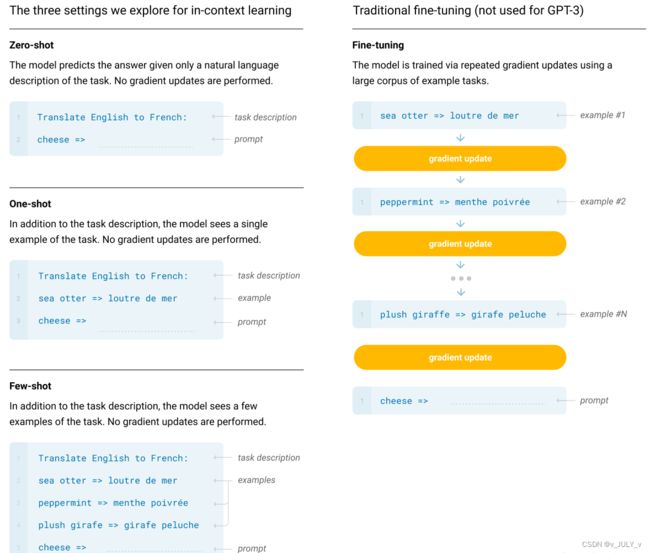
为形象描述,举一个GPT-3在只有少量样本下的机器翻译使用范例,如下图
- 图中右侧是普通模型微调的过程,模型通过大量训练预料进行训练,然后基于特定的任务数据进行梯度迭代更新(gradient update),训练至收敛后的模型才具备良好的翻译能力
- 图中左侧是GPT3分别在0样本(只给出任务描述)、单样本(只给出任务描述+一个翻译样本)、小样本(给出任务描述+少量样本)的情况下所展示出的能力,即便是小样本的情况下,也远少于微调过程所需要的训练数据
说白了,就是在同等训练数据下,GPT的性能远高于微调模式的SOTA模型
至此,我们对比下Fine-tuning和prompt learning的区别就是从Pre-train、Fine-tune到Pre-train、Prompt、Predict的过程
- Fine-tuning中:是预训练语言模型“迁就“各种下游任务。具体体现就是通过引入各种辅助任务loss,将其添加到预训练模型中,然后继续pre-training,以便让其更加适配下游任务。总之,这个过程中,预训练语言模型做出了更多的牺牲
- Prompting中,是各种下游任务“迁就“预训练语言模型。我们需要对不同任务进行重构,使得它达到适配预训练语言模型的效果。总之,这个过程中,是下游任务做出了更多的牺牲
1.4 GPT3.5:爆火ChatGPT所基于的GPT模型
考虑到下文要讲的instructGPT和ChatGPT分别预计GPT3、GPT3.5,所以本文还得再讲下GPT3.5相比GPT3的差别。
粗略的讲,GPT-3.5 模型使用与 GPT-3 相同的预训练数据集,但进行了额外的微调,从而更擅长以下两点
考虑到本文的主旨核心ChatGPT用到了RLHF和PPO,所以本文的第二部分将从强化学习讲到PPO算法。
第二部分 从RL、策略梯度到PPO算法、逆强化学习
2.1 强化学习必须掌握的基础
2.1.1 什么是强化学习
强化学习里面的概念、公式,相比ML/DL特别多,初学者刚学RL时,很容易被接连不断的概念、公式给绕晕,而且经常忘记概念与公式符号表达的一一对应,为此,我建议学习RL的第一步就是一定要扎实关于RL的一些最基本的概念、公式(不要在扎实基础的阶段图快或图囵吞枣,不然后面得花更多的时间、更大的代价去弥补),且把概念与公式的一一对应关系牢记于心,这很重要。
当然,为最大限度的提高本文的可读性,我会尽可能的多举例、多配图。
但RL之外,像高等数学里的什么叫导数、多元函数、偏导数、以及AI一些最基本的概念比如损失函数、梯度/梯度下降等,可以直接Wikipedia上查看相关概念,本文则不赘述了,毕竟可以为通俗而增加篇幅,但不为了介绍而介绍式的增加篇幅,避免影响完读率,^_^。话休絮烦,下面开始正题。
强化学习(reinforcement learning,RL),基于智能体(agent)在复杂、不确定的环境(environment)中最大化它能获得的奖励,从而达到自主决策的目的。
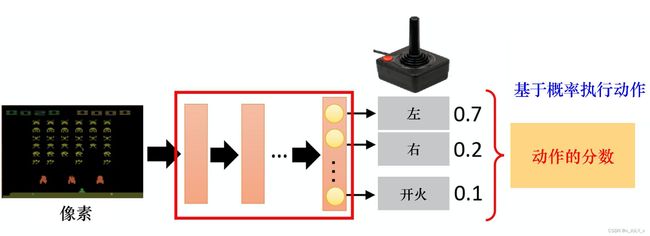
经典的强化学习模型可以总结为下图的形式(你可以理解为任何强化学习都包含这几个基本部分:智能体、行为、环境、状态、奖励):
一般的文章在介绍这些概念时很容易一带而过,这里我把每个概念都逐一解释下
- Agent,一般译为智能体,就是我们要训练的模型,类似玩超级玛丽的时候操纵马里奥做出相应的动作,而这个马里奥就是Agent
- action(简记为
 ),玩超级玛丽的时候你会控制马里奥做三个动作,即向左走、向右走和向上跳,而马里奥做的这三个动作就是action
),玩超级玛丽的时候你会控制马里奥做三个动作,即向左走、向右走和向上跳,而马里奥做的这三个动作就是action - Environment,即环境,它是提供reward的某个对象,它可以是AlphaGo中的人类棋手,也可以是自动驾驶中的人类驾驶员,甚至可以是某些游戏AI里的游戏规则
- reward(简记为
 ),这个奖赏可以类比为在明确目标的情况下,接近目标意味着做得好则奖,远离目标意味着做的不好则惩,最终达到收益/奖励最大化,且这个奖励是强化学习的核心
),这个奖赏可以类比为在明确目标的情况下,接近目标意味着做得好则奖,远离目标意味着做的不好则惩,最终达到收益/奖励最大化,且这个奖励是强化学习的核心 - State(简介为
 ),可以理解成状态或环境状态
),可以理解成状态或环境状态
总的而言,Agent通过感知环境Environment从而获取环境的状态state,进而依据策略决策从而执行动作action,最后得到奖励reward,然后再继续按此流程“感知状态-依据策略执行动作-得到奖励”循环进行。
另外,有两点值得一提
- 第一,不同状态出现的概率不一样(比如明天是天晴还是下雨不一定,即便看了天气预报也只是预测大概率是天晴而已),同一状态下执行不同动作的概率也不一样(比如即便在明天是天晴的概率下,你大概率不会带伞,但依然不排除你可能会防止突然下雨而带伞)
- 第二,另外,值得一提的是,人的一言一行会受到评估好优化言行,对于智能体也类似,比如有状态则有对状态的评估,有状态下执行的动作则有对状态下执行动作的评估,那怎么评估状态的价值、怎么评估状态下动作的价值呢?
于此,也就出来了所谓的状态价值函数、动作价值函数
最终一切评估结合奖励,毕竟我们的目的是需要最大化奖励,从而不断采取最优的策略,所谓最优策略就是在同一环境或不同环境下采取的最佳动作实践
进一步,具体而言,“感知状态-依据策略执行动作-得到奖励”的整个过程分为两步
- 第一步,它会根据当前状态State来采取动作action
我们会通过“状态价值函数”对当前状态进行评估,用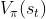 表示状态
表示状态 在策略
在策略 下的价值
下的价值
其中,采取什么样的动作就涉及到策略policy,策略函数可以表述为 函数(当然,这里的
函数(当然,这里的 跟圆周率没半毛钱关系),从而可得
跟圆周率没半毛钱关系),从而可得 ,意味着输入状态
,意味着输入状态 ,策略函数
,策略函数 输出动作
输出动作
此外,还会有这样的表述,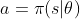 ,在输入状态
,在输入状态 确定的情况下,输出的动作
确定的情况下,输出的动作 只和后面的参数
只和后面的参数 有关,这个
有关,这个 就是策略函数
就是策略函数 的参数
的参数
再比如这种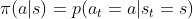 ,而这相当于输入一个状态
,而这相当于输入一个状态 下,智能体采取某个动作的概率,这个啥意思呢?意思是在状态
下,智能体采取某个动作的概率,这个啥意思呢?意思是在状态 确定之下,智能体采取不同动作的概率是不同的,比如当到了中午吃饭的时刻但家里没有食材了,这个时候你可能有50%的概率去买食材,也可能有30%的概率直接订外卖,最后有20%的概率到冰箱里随便找点吃的
确定之下,智能体采取不同动作的概率是不同的,比如当到了中午吃饭的时刻但家里没有食材了,这个时候你可能有50%的概率去买食材,也可能有30%的概率直接订外卖,最后有20%的概率到冰箱里随便找点吃的 - 第二步,记录被反馈的奖励reward,以便下次再到相同状态时能采取更优的动作
所谓奖励reward是指我们在当前状态采取了某个动作,可以得到多大的奖励
奖励函数是状态和动作的函数,即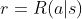 ,如果和这个公式结合起来
,如果和这个公式结合起来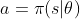 ,就是
,就是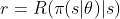 ,当然,当前状态的奖励一般看平均值即期望:
,当然,当前状态的奖励一般看平均值即期望: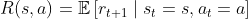
此外,实际中,因为一个状态可以得到的奖励是持久的(只是越往后某个事给的回报率越低,也即奖励因子越小,用折扣因子 表示)
表示)
举个例子,一个少年在面对“上大学、去打工、在家啃老”这三种状态,哪一种更能实现人生的价值呢?
相信很多人为长远发展都会选择上大学,因为身边有太多人因为上了大学,而好事连连,比如读研读博留学深造、进入大厂、娶个漂亮老婆、生个聪明孩子
当然了,上大学好处肯定多多,但上大学这个状态对上面4件好事所给予的贡献必然是逐级降低,毕竟越往后,越会有更多或更重要的因素成就后面的好事,总不能因为所有好事都百分百归功于最开头选择了“上大学”这个状态/决策嘛
且即便同一种状态下,不同策略下也会采取不同的动作,比如我希望最短时间内把柴砍完,如果我鼠目寸光可能会选择不磨刀直接砍,看似一开始柴被一个个劈开了 好像很快,但因为刀口有绣,实际全部砍完可能花了30分钟,但如果我明白磨刀不误砍柴工,则我可能花了1分钟磨刀,然后再用10分钟就把柴砍完了
这就涉及到“动作价值函数”对动作的评估,可以用 表示为状态
表示为状态 在策略
在策略 下选取动作
下选取动作 的价值,这就是大名鼎鼎的
的价值,这就是大名鼎鼎的 函数,得到
函数,得到 函数后,进入某个状态要采取的最优动作便可以通过Q函数得到,即
函数后,进入某个状态要采取的最优动作便可以通过Q函数得到,即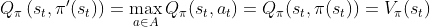
2.1.2 RL与监督学习的区别和RL方法的分类
此外,RL和监督学习(supervised learning)的区别:
- 监督学习有标签告诉算法什么样的输入对应着什么样的输出(譬如分类、回归等问题,一开始的分类不准没关系,通过建立损失函数+反向传播不断调整优化)
所以对于监督学习,目标是找到一个最优的模型函数,使其在训练数据集上最小化一个给定的损失函数,相当于最小化预测误差
最优模型 = arg minE_{(特征,标签)-数据分布} [损失函数(标签,模型(特征)]
RL没有标签告诉它在某种情况下应该做出什么样的行为,只有一个做出一系列行为后最终反馈回来的reward,然后判断当前选择的行为是好是坏
相当于RL的目标是最大化智能体策略在和动态环境交互过程中的价值,而策略的价值可以等价转换成奖励函数在策略的占用度量期望,即最大化累计下来的奖励期望
最优策略 = arg maxE(状态,动作)-策略的占用度量 [奖励函数(状态,动作)]
注,所谓占用度量是为了衡量一个智能体决策与动态环境的交互过程中,采样到一个具体的动作状态对(state-action pair)的概率分布 - 监督学习如果做了比较坏的选择则会立刻反馈给算法
RL的结果反馈有延时,有时候可能需要走了很多步以后才知道之前某步的选择是好还是坏 - 监督学习中输入是独立分布的,即各项数据之间没有关联
RL面对的输入总是在变化,每当算法做出一个行为,它就影响了下一次决策的输入
进一步,RL为得到最优策略从而获取最大化奖励,有
- 基于值函数的方法,通过求解一个状态或者状态下某个动作的估值为手段,从而寻找最佳的价值函数,找到价值函数后,再提取最佳策略
比如Q-learning、DQN等,适合离散的环境下,比如围棋和某些游戏领域
BTW,因为本文主旨ChatGPT用的RL算法是PPO,和Q-learning没有最直接的联系,所以本文不阐述Q-learning,但下一篇笔记强化学习极简入门会仔细讲 - 基于策略的方法,一般先进行策略评估,即对当前已经搜索到的策略函数进行估值,得到估值后,进行策略改进,不断重复这两步直至策略收敛
比如策略梯度法:PG算法policy gradient,适合连续动作的场景,比如机器人控制领域
以及Actor-Criti(一般被翻译为演员-评委算法),既学习价值函数,有学习策略函数,不过,Actor-Criti本质上是属于基于策略的算法,毕竟算法的目标是优化一个带参数的策略,只是会额外学习价值函数,从而帮助策略函数更好的学习
此外,还有对策略梯度算法的改进,比如TRPO算法、PPO算法,当然也有的文章会把PPO算法称之为是一种Actor-Critic架构,本文会重点阐述
2.1.3 RL的两个关键概念:马尔科夫、KL散度
RL通常是一个马尔科夫决策过程,但何谓马尔科夫呢?据强化学习2一书的第47页所说
在马尔科夫决策过程中,
和
的每个可能的值出现的概率只取决于前一个状态
和前一个动作
,并且与更早之前的状态和动作完全无关,这个限制不是针对决策过程,而是针对状态的,状态必须包括过去智能体和环境交互的方方面面的信息,这些信息会对未来产生一定影响,这样,状态就被认为具有马尔科夫性。
换言之,下一步的状态取决于当前的状态以及当前采取的动作。它由状态转移概率和奖励函数两个部分组成
- 状态转移概率即
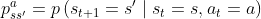
- 奖励函数即
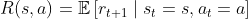
当我们有了策略、价值函数和模型3个组成部分后,就形成了一个马尔可夫决策过程(Markov decision process)。如下图所示,这个决策过程可视化了状态之间的转移以及采取的动作。
接下来,再介绍下KL散度,KL 散度衡量两个数据分布![]() 和
和![]() 之间的差异。
之间的差异。
![]()
我们将其重新用于衡量两个分布之间的差异
2.3 策略梯度与其两个问题:采样效率低下与步长难以确定
2.3.1 什么是策略梯度和梯度计算/更新的流程
本节推导的核心内容参考自Easy RL教程等资料(但修正了原教程上部分不太准确的描述,并补充了大量的解释说明和部分公式的拆解细节)。另,都说多一个公式则少一个读者,本文要打破这点,虽然本节推导很多,但每一步推导都有介绍到,不会省略任何一步推导,故不用担心看不懂(对本文任何内容有任何问题,都欢迎随时留言评论)。
策略梯度的核心算法思想是:参数为![]() 的策略
的策略![]() 接受状态
接受状态![]() ,输出动作概率分布,在动作概率分布中采样动作,执行动作(形成运动轨迹
,输出动作概率分布,在动作概率分布中采样动作,执行动作(形成运动轨迹![]() ),得到奖励
),得到奖励![]() ,跳到下一个状态。在这样的步骤下,我们可以使用策略
,跳到下一个状态。在这样的步骤下,我们可以使用策略![]() 收集一批样本,然后使用梯度下降算法学习这些样本,不过当策略
收集一批样本,然后使用梯度下降算法学习这些样本,不过当策略![]() 的参数更新后,这些样本不能继续被使用,还要重新使用策略
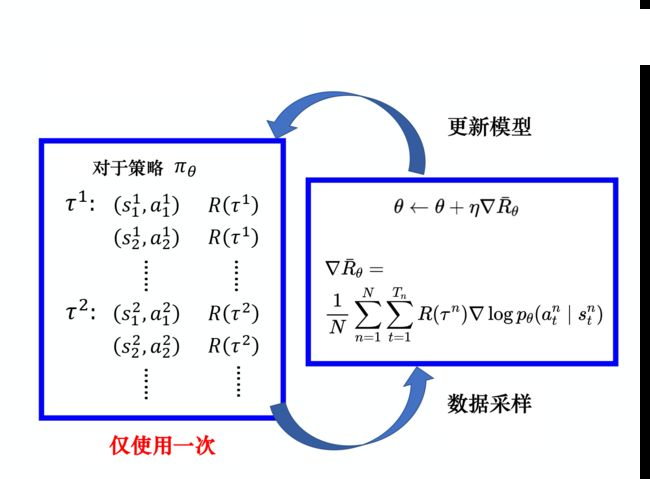
的参数更新后,这些样本不能继续被使用,还要重新使用策略![]() 与环境互动收集数据。类似下图所示(下图以及本节大部分配图/公式均来自easy RL教程)
与环境互动收集数据。类似下图所示(下图以及本节大部分配图/公式均来自easy RL教程)
接下来,详细阐述。首先,我们已经知道了策略函数可以如此表示:![]() ,如何评价策略的好坏呢?
,如何评价策略的好坏呢?
假设机器人在策略![]() 的决策下,形成如下的运动轨迹(类似你玩三国争霸时,你控制角色在各种不同的游戏画面/场景/状态下作出一系列动作,而当完成了系统布置的某个任务时则会得到系统给的奖励,如此,运动轨迹用
的决策下,形成如下的运动轨迹(类似你玩三国争霸时,你控制角色在各种不同的游戏画面/场景/状态下作出一系列动作,而当完成了系统布置的某个任务时则会得到系统给的奖励,如此,运动轨迹用 ![]() 表示,从而
表示,从而![]() 表示为一个状态
表示为一个状态![]() 、动作
、动作![]() 、奖励值
、奖励值![]() 不断迁移的过程)
不断迁移的过程)
![]()
给定智能体或演员的参数![]() ,我们可以计算某一条轨迹
,我们可以计算某一条轨迹![]() 发生的概率为
发生的概率为
那策略的评价函数便可以设为(以![]() 为参数的策略
为参数的策略![]() 的条件下,产生一系列奖励值,且为客观综合起见,最终取的是多个策略的平均值,即总奖励
的条件下,产生一系列奖励值,且为客观综合起见,最终取的是多个策略的平均值,即总奖励![]() 的数学期望
的数学期望![]() )
)
![]()
其中,![]() 可以理解为一个我们所熟知的神经网络
可以理解为一个我们所熟知的神经网络
- 当你对神经网络有所了解的话,你一定知道通过梯度下降求解损失函数的极小值(忘了的,可以复习下:首先通过正向传播产生拟合值,与标签值做“差”计算,产生误差值,然后对误差值求和产生损失函数,最后对损失函数用梯度下降法求极小值,而优化的对象就是神经网络的参数
 )
) - 类比到
 这个问题上,我们现在是正向传播产生动作,然后动作在环境中产生奖励值,通过奖励值求和产生评价函数,气氛都到这了,此时是不可以针对评价函数做梯度上升(gradient ascent)呢?毕竟能求极小值,便能求极大值,正如误差能最小化,奖励/得分就能最大化
这个问题上,我们现在是正向传播产生动作,然后动作在环境中产生奖励值,通过奖励值求和产生评价函数,气氛都到这了,此时是不可以针对评价函数做梯度上升(gradient ascent)呢?毕竟能求极小值,便能求极大值,正如误差能最小化,奖励/得分就能最大化
好手段,接下来我们把上面的![]() 改写一下。由于每一个轨迹
改写一下。由于每一个轨迹 ![]() 都有一个概率,所以我们要计算总奖励便得穷举所有可能的轨迹
都有一个概率,所以我们要计算总奖励便得穷举所有可能的轨迹 ![]() ,然后对所有
,然后对所有![]() 出现的概率进行加权并求和出总期望值:
出现的概率进行加权并求和出总期望值:
上述整个过程如下图所示
通过上文我们已经知道,想让奖励越大越好,可以使用梯度上升来最大化期望奖励。而要进行梯度上升,我们先要计算期望奖励![]() 的梯度。
的梯度。
我们对 ![]() 做梯度运算(其中,只有
做梯度运算(其中,只有 ![]() 与
与 ![]() 有关。Em,忘了什么是梯度的,可以通过这个梯度的Wikipedia页面复习下)
有关。Em,忘了什么是梯度的,可以通过这个梯度的Wikipedia页面复习下)
![]()
考虑到![]() ,可得
,可得
从而进一步转化,可得![]()
Em,怎么来的?别急,具体推导是,第一步 先分母分子都乘以一个
,第二步 把上面公式代入计算,第三步 做个简单转换
然不巧的是,期望值 ![]() 无法计算,所以我们只能用采样的方式采样 N 个
无法计算,所以我们只能用采样的方式采样 N 个![]() 并计算每一个的值,再把每一个的值加起来,如此得到梯度,即
并计算每一个的值,再把每一个的值加起来,如此得到梯度,即
任何必要的中间推导步骤咱不能省,所以还是要说明下。即,其中
的具体计算过程是
完美!我们可以直观地理解上面![]() 的梯度计算公式
的梯度计算公式
- 即在我们采样到的数据里面,采样到在某一个状态
 要执行某一个动作
要执行某一个动作 ,
,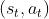 是在整个轨迹
是在整个轨迹 的里面的某一个状态和动作的对
的里面的某一个状态和动作的对 - 假设我们在
 执行
执行 ,最后发现
,最后发现 的奖励是正的,我们就要增加在
的奖励是正的,我们就要增加在  执行
执行  的概率。反之,如果在
的概率。反之,如果在 执行
执行  会导致
会导致  的奖励变成负的, 我们就要减少在
的奖励变成负的, 我们就要减少在  执行
执行  的概率。这怎么实现呢?
的概率。这怎么实现呢? - 我们用梯度上升来更新参数,原来有一个参数
 ,把
,把  加上梯度
加上梯度 ,当然我们要有一个学习率
,当然我们要有一个学习率  ,学习率也是要调整的,可用 Adam、RMSProp 等方法来调整学习率,即
,学习率也是要调整的,可用 Adam、RMSProp 等方法来调整学习率,即
![]()
总之,至此,我们已经得到了
的梯度计算的公式
有一点值得说明的是...,为了提高可读性,还是举个例子来说明吧。
比如到80/90后上大学时喜欢玩的另一个游戏CF(即cross fire,10多年前我在东华理工的时候也经常玩这个,另一个是DNF),虽然玩的是同一个主题比如沙漠战场,但你每场的发挥是不一样的,即便玩到同一个地方(比如A区埋雷的地方),你也可能会控制角色用不同的策略做出不同的动作,比如
- 在第一场游戏里面,我们在状态
采取动作
,在状态
采取动作
。且你在同样的状态
下,不是每次都会采取动作
的,所以我们要记录,在状态
采取
、在状态
采取
等,整场游戏结束以后,得到的奖励是
- 在第二场游戏里面,在状态
采取
,在状态
采取
,我们采样到的就是
,得到的奖励是
这时我们就可以把采样到的数据用梯度计算公式把梯度算出来
2.3.2 重要性采样(为采样q解决p从而增加重要性权重):解决策略梯度采样效率低下
这显然是非常花时间的,怎么解决这个问题呢?
首先,我们先来明确两个概念:
- 如果要学习的智能体和与环境交互的智能体是相同的,我们称之为同策略
- 如果要学习的智能体和与环境交互的智能体不是相同的,我们称之为异策略
回到策略梯度这个采样到的数据只能使用一次的问题,是否可以把同策略模式转变成异策略模式呢?
- 想要从同策略变成异策略,这样就可以用另外一个策略
 、另外一个演员
、另外一个演员 与环境交互(
与环境交互( 被固定了),用
被固定了),用 采样到的数据去训练
采样到的数据去训练
- 假设我们可以用
 采样到的数据去训练
采样到的数据去训练 ,我们可以多次使用
,我们可以多次使用 采样到的数据,可以多次执行梯度上升(gradient ascent),可以多次更新参数, 都只需要用
采样到的数据,可以多次执行梯度上升(gradient ascent),可以多次更新参数, 都只需要用 采样到的同一批数据
采样到的同一批数据
这个过程具体的做法就叫重要性采样,即通过使用另外一种分布,来逼近所求分布的一种方法。
为备忘,我把2.3.1节得出的
梯度计算的公式再贴一下
基于重要性采样的原则,我们用另外一个策略![]() ,它就是另外一个演员,与环境做互动采样数据来训练
,它就是另外一个演员,与环境做互动采样数据来训练![]() ,从而间接计算
,从而间接计算![]()
但具体怎么操作呢?为说明怎么变换的问题,再举一个例子。
假设有一个函数
,
需要从分布
中采样,我们应该如何怎么计算()的期望值呢?
如果分布
不能做积分,那么只能从分布
尽可能多采样更多的
,然后全都代入到
,取它的平均值就可以得到近似()的期望值:
当不能在分布
中采样数据,而只能从另外一个分布
中去采样数据时(
可以是任何分布),就需要做些变换。
整理下可得(左边是分布
,右边是分布
):
如此,我们便就可以从
里面采样
,再计算
,再取期望值。所以就算我们不能从
里面采样数据,但只要能从
里面采样数据,就可以计算从
采样
然后代入
以后的期望值。
类似的,当转用![]() 去采样数据训练
去采样数据训练![]() 后,得在
后,得在![]() 的基础上补上一个重要性权重:
的基础上补上一个重要性权重:![]() ,相当于原来的
,相当于原来的![]() 分布相当于变成了
分布相当于变成了![]() 。这个重要性权重针对某一个轨迹
。这个重要性权重针对某一个轨迹![]() 用
用![]() 算出来的概率除以这个轨迹
算出来的概率除以这个轨迹![]() 用
用![]() 算出来的概率。
算出来的概率。
最终加上重要性权重之后,可得
怎么来的?完整推导如下
梯度的计算好像差不多了?但实际在做策略梯度的时候,并不是给整个轨迹![]() 都一样的分数,而是每一个状态-动作的对会分开来计算,那具体怎么抽样呢?
都一样的分数,而是每一个状态-动作的对会分开来计算,那具体怎么抽样呢?
实际上更新梯度的时候,如下式所示( 我们用演员![]() 去采样出
去采样出![]() 跟
跟![]() ,采样出状态跟动作的对
,采样出状态跟动作的对![]() ,并计算这个状态跟动作对的优势
,并计算这个状态跟动作对的优势![]() )
)
![]()
其中,![]() 要估测的是在状态
要估测的是在状态![]() 采取动作
采取动作![]() 是好的还是不好的:即如果
是好的还是不好的:即如果![]() 是正的,就要增加概率;如果是负的,就要减少概率。
是正的,就要增加概率;如果是负的,就要减少概率。
不过,![]() 是演员
是演员![]() 与环境交互的时候计算出来的,基于重要性采样的原则,现在当从
与环境交互的时候计算出来的,基于重要性采样的原则,现在当从 ![]() 换到
换到 ![]() 的时候,就需要在
的时候,就需要在
![]()
基础上, ![]() 变换成
变换成![]() ,一变换便得加个重要性权重(即把
,一变换便得加个重要性权重(即把![]() 、
、![]() 用
用![]() 采样出来的概率除掉
采样出来的概率除掉 ![]() 、
、![]() 用
用![]() 采样出来的概率),公式如下(Easy RL原书上把下面公式中的
采样出来的概率),公式如下(Easy RL原书上把下面公式中的![]() 写成了
写成了![]() )
)
接下来,我们可以拆解![]() 和
和![]() ,即
,即
于是可得公式
这里需要做一件事情,假设模型是![]() 的时候,我们看到
的时候,我们看到![]() 的概率,跟模型是
的概率,跟模型是![]() 的时候,看到
的时候,看到![]() 的概率是差不多的,即
的概率是差不多的,即![]() 。
。
为什么可以这样假设呢?一种直观的解释就是
很难算,这一项有一个参数
,需要拿
去跟环境做互动,算
出现的概率。 尤其是如果输入是图片的话,同样的
根本就不会出现第二次。我们根本没有办法估这一项,所以就直接无视这个问题。
但是
是很好算,我们有
这个参数,它就是个网络。我们就把
带进去,
就是游戏画面。 我们有个策略的网络,输入状态
,它会输出每一个
的概率。所以,我们只要知道
和
的参数就可以算
。
所以,实际上在更新参数的时候,我们就是按照下式来更新参数:
所以实际上,我们可以从梯度![]() 来反推目标函数,当使用重要性采样的时候,要去优化的目标函数如下式所示,我们把它记
来反推目标函数,当使用重要性采样的时候,要去优化的目标函数如下式所示,我们把它记![]()
终于大功告成!
2.3.3 重要性采样的问题:无法解决两个分布差距大的问题
好巧不巧,看似大功告成了,但重要性采样还是有个问题。具体什么问题呢,为更好的说明这个问题,我们回到上文的那个例子中。
还是那两个分布:
、
,不能从
里面采样数据,但只要能从
里面采样数据基于重要性采样的原则,虽然我们可以把
换成任何的
,但是在实现上,
和
的差距不能太大。差距太大,会出问题。
比如,虽然上述公式成立,但如果不是计算期望值,而是计算方差,
和
是不一样的。因为两个随机变量的平均值相同,并不代表它们的方差相同。此话怎讲?以下是推导过程:
我们可以将
、分别
代入方差的公式
,则分别可得(且考虑到不排除会有比初级更初级的初学者学习本文,故把第二个公式拆解的相对较细)
所以结论就是,如果我们只要对分布![]() 采样足够多次,对分布
采样足够多次,对分布![]() 采样足够多次,得到的期望值会是一样的。但是如果我们采样的次数不够多,会因为它们的方差差距可能是很大的,所以就可能得到差别非常大的结果。
采样足够多次,得到的期望值会是一样的。但是如果我们采样的次数不够多,会因为它们的方差差距可能是很大的,所以就可能得到差别非常大的结果。
那怎么办呢?这就引出了:为解决两个分布差距大的问题,TRPO/PPO都增加了一个KL散度约束。
2.3.4 基于KL散度和信任区域的TRPO:解决两个分布相差大和步长难以确定的问题
考虑到重要性采样有一个问题:如果 ![]() 与
与 ![]() 相差太多,即这两个分布相差太多,重要性采样的结果就会不好。怎么避免它们相差太多呢?这就是TRPO算法所要解决的
相差太多,即这两个分布相差太多,重要性采样的结果就会不好。怎么避免它们相差太多呢?这就是TRPO算法所要解决的
2015年John Schulman等人提出了信任区域策略优化(trust region policyopimization, TRPO),本质上,TRPO的出现解决了两个问题,一个解决重要性采样中两个分布差距太大的问题,一个是解决策略梯度算法中步长难以确定的问题
- 关于前者,在2.3.2节得到的目标函数基础上(下图第一个公式),增加了一个KL散度约束(如下图第二个公式)
至此采样效率低效的问题通过重要性采样(重要性权重)、以及增加KL散度约束解决了(关于KL散度约束的意义会在下文2.4节深入阐述) - 关于后者,具体而言,当策略网络是深度模型时,沿着策略梯度更新参数,很有可能由于步长太长,策略突然显著变差,进而影响训练效果
这是2.3.1节,我们已经得到的梯度计算和梯度更新公式

针对这个问题,我们考虑在更新时找到一块信任区域(trust region),在这个区域上更新策略时能够得到某种策略性能的安全性保证,这就是TRPO算法的主要思想
为进一步阐述后者,举个例子,比如爬两面都是悬崖的山。你首先选择最陡峭的方向,然后向前移动一个步长。如果步长太小,则需要很长时间才能到达峰值。但如果它太大,我们就会掉下悬崖。
信任域中的最大步长是多少?在信赖域方法中,我们从初始猜测开始可选地,然后动态地重新调整区域大小。例如,如果新政策和当前政策的差异越来越大,我们可以缩小信赖区域。
所以TRPO就是考虑到连续动作空间无法每一个动作都搜索一遍,因此大部分情况下只能靠猜。如果要猜,就最好在信任域内部去猜。而TRPO将每一次对策略的更新都限制了信任域内,从而极大地增强了训练的稳定性。
至此,PG算法的采样效率低下、步长难以确定的问题都被我们通过TRPO给解决了。但TRPO的问题在哪呢?
TRPO的问题在于把 KL 散度约束当作一个额外的约束,没有放在目标里面,导致TRPO很难计算,总之因为信任域的计算量太大了,John Schulman等人于2017年又推出了TRPO的改进算法:PPO
2.4 近端策略优化PPO:解决TRPO的计算量大的问题
2.4.1 什么是近端策略优化PPO
如上所述,PPO算法是针对TRPO计算量的大的问题提出来的,和TRPO一样也用上了KL散度约束,但PPO的改进在于把KL散度约束直接放在了目标函数里。
- PPO 需要优化目标函数
 ,让其最大化
,让其最大化
但是这个目标函数又牵涉到重要性采样。在做重要性采样的时候, 不能与
不能与 相差太多。做示范的模型不能与真正的模型相差太多,相差太多,重要性采样的结果就会不好
相差太多。做示范的模型不能与真正的模型相差太多,相差太多,重要性采样的结果就会不好 - 所以在训练的时候,应多加一个约束(constrain):Jθ′(θ)=Jθ′(θ)−βKL(θ,θ′)。这个约束是
 与
与  输出的动作的 KL 散度(KL divergence),这一项用于衡量
输出的动作的 KL 散度(KL divergence),这一项用于衡量  与
与  的相似程度。我们希望在训练的过程中,学习出的
的相似程度。我们希望在训练的过程中,学习出的  与
与  越相似越好。因为如果
越相似越好。因为如果  与
与  不相似,最后的结果就会不好。
不相似,最后的结果就会不好。
所以在 PPO 里面有两项:一项是优化本来要优化的![]() ,另一项是一个约束。这个约束就好像正则化(regularization)的项(term) 一样,它所做的就是希望最后学习出的
,另一项是一个约束。这个约束就好像正则化(regularization)的项(term) 一样,它所做的就是希望最后学习出的 ![]() 与
与 ![]() 相差不大,如下所示
相差不大,如下所示
当然,你也也可以把上述那两个式子合二为一为(可以更直观的看出,PPO把约束作为惩罚项放在目标函数中,从而可以用梯度上升的方法去最大化它。
2.4.2 PPO算法的两个主要变种:PPO-penalty与PPO-clip
PPO 算法有两个主要的变种:近端策略优化惩罚(PPO-penalty)和近端策略优化裁剪(PPO-clip)。
我们先来看下近端策略优化惩罚PPO-penalty
- 它先初始化一个策略的参数
 。在每一个迭代里面,我们用前一个训练的迭代得到的actor的参数
。在每一个迭代里面,我们用前一个训练的迭代得到的actor的参数 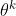 与环境交互,采样到大量状态-动作对。
与环境交互,采样到大量状态-动作对。 - 根据
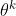 交互的结果,我们估测
交互的结果,我们估测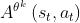
- 最后我们使用 PPO 的优化公式:
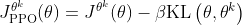
上文有一个细节并没有讲到,即![]() 是怎么取值的呢,关于
是怎么取值的呢,关于![]() 的设置有一个动态调整
的设置有一个动态调整![]() 的方法,具体而言
的方法,具体而言
- 我们先设一个可以接受的 KL 散度的最大值。假设优化完
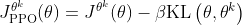 以后,KL 散度的值太大,这就代表后面惩罚的项
以后,KL 散度的值太大,这就代表后面惩罚的项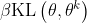 没有发挥作用,我们就把
没有发挥作用,我们就把 增大
增大 - 我们设一个 KL 散度的最小值。如果优化完式
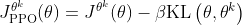 以后,KL 散度比最小值还要小,就代表后面这一项的效果太强了,我们怕他只优化后一项,使
以后,KL 散度比最小值还要小,就代表后面这一项的效果太强了,我们怕他只优化后一项,使 与
与 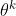 一样,这不是我们想要的,所以我们要减小
一样,这不是我们想要的,所以我们要减小 。
。
综上,![]() 是可以动态调整的,因此我们称之为自适应KL惩罚(adaptive KL penalty)。最后,总结一下自适应KL惩罚:
是可以动态调整的,因此我们称之为自适应KL惩罚(adaptive KL penalty)。最后,总结一下自适应KL惩罚:
- 如果
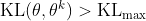 ,增大
,增大  ;
; - 如果
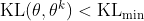 ,减小
,减小  。
。
近端策略优化惩罚可表示为
最后,如果我们觉得计算 KL散度很复杂,那么还有一个 PPO2算法,PPO2 即近端策略优化裁剪。近端策略优化裁剪的目标函数里面没有 KL 散度,其要最大化的目标函数为
整个目标函数在![]() 这个大括号里有两部分,最终对比两部分那部分更小,就取哪部分的值,这么做的本质目标就是为了让
这个大括号里有两部分,最终对比两部分那部分更小,就取哪部分的值,这么做的本质目标就是为了让![]() 和
和![]() 可以尽可能接近,不至差距太大。
可以尽可能接近,不至差距太大。
第一部分我们已经见过了,好理解,咱们来重点分析公式的第二部分
- 首先是
 括号里的部分,如果用一句话简要阐述下其核心含义就是:如果
括号里的部分,如果用一句话简要阐述下其核心含义就是:如果 和
和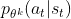 之间的概率比落在范围
之间的概率比落在范围 和
和 之外,
之外, 将被剪裁,使得其值最小不小于
将被剪裁,使得其值最小不小于 ,最大不大于
,最大不大于
- 然后是
 括号外乘以个状态-动作对
括号外乘以个状态-动作对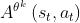 ,如果
,如果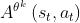 大于0,则说明这是好动作,需要增大
大于0,则说明这是好动作,需要增大 ,但
,但 最大不能超过
最大不能超过 ;如果
;如果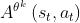 小于0,则说明该动作不是好动作,需要减小
小于0,则说明该动作不是好动作,需要减小 ,但
,但 最小不能小过
最小不能小过
具体而言,针对目标函数
反之,如果
小于0,则最终目标函数的取值为了更小则和
大于0时反过来,毕竟加了个负号自然一切就不同了,为方便初学者一目了然,咱们还是把计算过程列出来,即
2.5 从RL到逆强化学习:聊天对话等场景中不好定义reward
强化学习理论上可以不需要大量标注数据,然而实际上它所需求的reward存在一些缺陷,这导致强化学习策略很难推广:
-
reward的制定非常困难,比如说游戏AI中,可能要制定成百上千条游戏规则,这并不比标注大量数据来得容易
-
部分场景下reward的效果不好,比如说自动驾驶的多步决策(sequential decision)场景中,学习器很难频繁地获得reward,容易累计误差导致一些严重的事故
-
再比如聊天机器人方面,我们不好定义什么是好的对话、什么是不好的对话,但我们可以收集很多人类的对话当做范例,如此,模仿学习(Imitation Learning)应运而生。
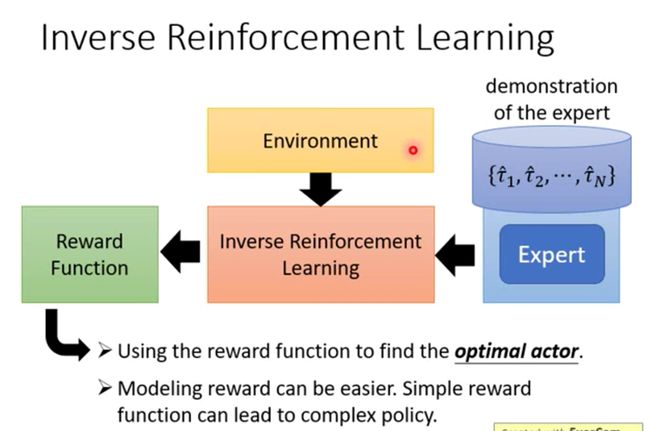
模仿学习的思路是不让模型在人类制定的规则下自己学习,而是让模型模仿人类的行为。而逆强化学习就是模仿学习的其中一种,何谓逆强化学习呢?
- 原来的强化学习里,有Environment和Reward Model,但逆强化学习刚好是相反的,它没有奖励函数,只有一些人类/专家的示范,当然,它还是有环境的
- 换言之,逆强化学习将强化学习的Environment替换成一个Reward Model,而这个RM是通过人类标注数据去训练得到
- 进一步,有了环境和人类标注数据以后,可以反推出奖励函数
总之,强化学习是由奖励函数推出什么样的动作/策略是最好的,逆强化学习则反过来
- 我们有人类标注数据,我们相信它是不错的,我就反推,人类因为什么样的奖励函数才会采取这些行为
- 有了奖励函数以后,接下来,我们就可以使用一般的强化学习的方法去找出最优策略/动作
所以逆强化学习是先找出奖励函数,找出奖励函数以后,再用强化学习找出最优策略/动作。
第三部分 instructGPT/ChatGPT的训练三阶段到多轮对话应用
3.1 InstructGPT训练三阶段
3.1.1 ChatGPT的前身之InstructGPT:基于RLHF手段微调的GPT
根据instructGPT的原始论文可知,InstructGPT的训练分为三个阶段(总体上结合了监督学习和强化学习,先是监督学习让GPT3有一个大致的微调方向,然后用RL中的PPO算法来更新微调过的GPT3的参数):
![]()
-
阶段1:利用人类的标注数据(demonstration data)去对GPT3进行有监督训练
首先,OpenAI是先设计了一个prompt dataset,里面有大量的提示样本,给出了各种各样的任务描述
其次,找了一个标注团队对这个prompt dataset进行标注(本质就是人工回答问题)
最后,用这个标注过的数据集微调GPT3,这个微调好的GPT3我们称之为SFT模型(监督微调,全称Supervised fine-tuning,简称SFT),具备了最基本的预测能力
BTW,相信你还记得上文1.3节所说的GPT3通过prompt learning在小样本下令人惊艳的表现,另再说句题外话,咱们训练的最终目标就是通过不断缩小instructGPT与人类预测之间的差距,从而不断提高instructGPT的预测能力 -
阶段2:训练奖励模型RM
把微调好的SFT模型去回答prompt dataset某个问题,然后通过收集4个不同的SFT输出而获取4个回答,接着人工对这4个回答的好坏进行标注且排序,排序的结果用来训练一个奖励模型RM,具体做法就是学习排序结果从而理解人类的偏好 -
阶段3:通过训练好的RM模型预测结果且通过PPO算法优化SFT模型策略
具体做法是,再次让SFT模型去回答prompt dataset某个问题,然后此时不再让人工评估好坏,而是让阶段2训练好的奖励模型去给SFT模型的预测结果进行打分排序
就这样,一个初始的语言模型SFT模型来生成文本,以及一个奖励模型(RM)来判断模型生成的文本是否优质(迎合人类偏好),然后不断生成、不断评估,交替进行
此外,可能有读者疑问,InstructGPT为什么要做这样的改进,或者说它的novelty是什么?
- 事实上,这个改进思路,一方面是为了尽可能地对齐(Alignment)GPT的输出与对用户友好的语言逻辑,即微调出一个用户友好型GPT。以往的GPT训练,都是基于大量无标注的语料,这些语料通常收集自充斥大量“行话”、“黑话”的互联网中,这样训练出来的语言模型,它可能会有虚假的、恶意的或者有负面情绪等问题的输出,二方面,为了更好的理解人类的意图
- 因此,一个直接的思路就是通过人工干预微调GPT,使其输出对用户友好(避免乱说话),且更好的理解人类意图并和人类对话
所以,对InstructGPT的简单理解,可以是基于人类反馈的强化学习(RLHF)手段微调的GPT。
值得一提的是,这个训练过程是不和我们逆向强化学习很熟?
为什么呢,因为强化学习是利用奖励学习策略,而所谓的逆向强化学习一般是从策略中反推奖励函数,对应到这个instructGPT的训练过程中,它通过人类专家的行为逆向强化学习出一个奖励函数,最后再利用这个奖励函数进行强化学习训练,这不是很眼熟
这里先提一嘴,下文会再具体阐述
3.1.2 ChatGPT与InstructGPT的差别:基于GPT3还是GPT3.5微调
而通过OpenAI公布的ChatGPT训练图可知,ChatGPT的训练流程与InstructGPT是一致的,差异只在于
- InstructGPT是在GPT-3上做Fine-Tune
- ChatGPT是在GPT-3.5上做Fine-Tune(GPT3.5是OpenAI在2021年Q4训练的InstructGPT模型,在自动编写代码方面有较强的能力)
接下来,我们分别具体阐述上面的阶段2、阶段3。
这里插个观点。自AlphaGo使得强化学习猛然进入大众视野以来,大部分对于强化学习的理论研究都将游戏作为主要实验平台,这一点不无道理,强化学习理论上的推导看似逻辑通顺,但其最大的弱点在于,基于人工评判的奖励 Reward 的获得,让实验人员守在电脑前对模型吐出来的结果不停地打分看来是不现实的,游戏系统恰恰能会给出正确客观的打分(输/赢 或 游戏Score)。
基于RL的对话生成同样会面对这个问题,研究人员采用了类似AlphaGo的实现方式(AI棋手对弈)——同时运行两个机器人,让它们自己互相对话,同时,使用预训练(pre-trained)好的“打分器”给出每组对话的奖励得分
,关于这个预训练的“打分器” R ,可以根据实际的应用和需求自己DIY,是否通顺是否辞不达意是否总说重复的废话
3.1.3 instructGPT训练阶段2:如何对多个输出排序及如何训练RM模型
可能又有读者有疑问了,即instructGPT中,人类对模型的多个输出做个排序,为什么就能够提供监督信号,或者说在训练RM时如何怎么做到loss的梯度回传?
训练RM的核心是由人类对SFT生成的多个输出(基于同一个输入)进行排序,再用来训练RM。按照模仿学习的定义,直观上的理解可以是,RM在模仿人类对语句的排序思路,或者按照参考文献,即Google DeepMind和OpenAI团队2017年的论文《Deep reinforcement learning from human preferences》的说法是,模仿人类的偏好(Preference)。
那么到底是如何模仿的呢,或者说如何实现梯度回传?
这里我们代入一个场景,假设你向一个六岁小孩解释什么是登陆月球或什么是RL,如下图
- SFT生成了ABCD四个回答语句,然后人类对照着Prompt输入(即提问)来对4个回答的好坏做出合适的排序,如D>C>A=B
- 这里的排序实质是人类分别给4个回答语句打分,比如对D打了7分,C打了6分,A和B打了4分
- 为了让RM学到人类偏好(即排序),可以四个语句两两组合分别计算loss再相加取均值,即分别计算
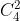 个即6个loss,具体的loss形式如下图:
个即6个loss,具体的loss形式如下图:
针对这个损失函数需要逐一说明的是
- 这是一个常见的排序模型,其中
 是提示Prompt输入,
是提示Prompt输入,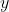 是SFT的预测输出,因为答案得跟着问题,所以问题答案的输出是一对输出,比如(
是SFT的预测输出,因为答案得跟着问题,所以问题答案的输出是一对输出,比如( ,
,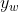 )、(
)、( ,
, ),
),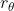 是RM模型,K是对多少个答案进行排序,实际处理是针对每个prompt生成
是RM模型,K是对多少个答案进行排序,实际处理是针对每个prompt生成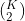 个比较,比如4个输出有6次比较,9个输出有36次比较,
个比较,比如4个输出有6次比较,9个输出有36次比较, 是人类比较的数据集。
是人类比较的数据集。
有一点要提下的是,RLHF中的rank就好比监督学习中的弱标注——它并不提供直接的监督信号。但通过学习简单的排序,RM可以学到人类的偏好
为何是排序,而非直接打分呢,道理很简单,排序相比打分更容易接近客观事实,即不同的标注员,打分的偏好会有很大的差异(比如同样一段精彩的文本,有人认为可以打1.0,但有人认为只能打0.8),而这种差异就会导致出现大量的噪声样本,若改成标注排序,则不同的标注员的排序一致性相比打分一致性就大大提升了
再打个比方,有一家冰箱工厂生产了好几种类型的冰箱,虽然这些客户中没有一个懂得如何造冰箱的(或者说他们不需要懂),但他们可以通过消费者的各类行为(点赞/评价、复购等),让厂商明白消费者对冰箱类型的“偏好”,从而引导冰箱厂商生产销量更好的冰箱
所以说,一个非专家的普通人类无法向一个6岁小孩解释清楚什么是RL,但他总能从多个备选答案判断出哪一个答案更好吧,毕竟选择比创造更容易啊!多么有创造性的解决方案 - 首先把你的问题
 和答案
和答案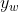 放进奖励函数r中,再把问题
放进奖励函数r中,再把问题 和
和 也放进奖励函数
也放进奖励函数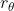 中,然后分别输出,假定
中,然后分别输出,假定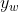 是语句组合对中相对
是语句组合对中相对 打分更高的,所以两者一减(这里面使用的是交叉熵损失函数,奖励的差异表示一种应答比另一种应答更受人类标注者青睐的对数概率),我们希望相减的结果越大越好
打分更高的,所以两者一减(这里面使用的是交叉熵损失函数,奖励的差异表示一种应答比另一种应答更受人类标注者青睐的对数概率),我们希望相减的结果越大越好 - 最后通过Logitech函数变成一个loss函数,而因为loss函数最前面加了一个负号,相当于最大化上面第2点最后相减的结果
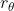 (
( ,
,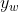 ) −
) − 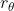 (
( ,
, )等于是最小化这个loss函数
)等于是最小化这个loss函数
如此,通过这种形式的梯度回传,RM逐渐学会了给D这类语句打高分,给A、B这类语句打低分,从而模仿到了人类偏好。到了这一步,不妨可以这么简单理解RLHF:所谓的人类反馈的强化学习,某种意义上来说,就是由人类的打分来充当reward。
3.1.4 instructGPT训练阶段3:如何通过PPO算法进一步优化策略模型
instructGPT原始论文中的目标函数如下图所示
![]()
大部分文章在分析这个目标函数时基本都是人云亦云、一带而过,在这里,我们逐一拆接下这个目标函数,分为三个部分
- 第一部分是
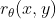 ,相当于根据人类偏好的学习出来的RM模型
,相当于根据人类偏好的学习出来的RM模型 - 第二部分则是用KL散度对比RL学到的策略模型
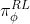 和原始策略模型
和原始策略模型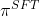 的某种差距,一开始时,
的某种差距,一开始时,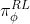 的初始化值就是
的初始化值就是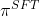 ,且咱们希望它俩之间的差距不至于太大(为啥?步子太大容易扯到那啥..)
,且咱们希望它俩之间的差距不至于太大(为啥?步子太大容易扯到那啥..)
这个时候你就可以用到PPO算法了,还记得PPO算法的用途么?
“我们可以通过重要性采样把同策略换成异策略,但重要性采样有一个问题:如果 与
与  相差太多,即这两个分布相差太多,重要性采样的结果就会不好。 怎么避免它们相差太多呢?这就是PPO要做的事情。”
相差太多,即这两个分布相差太多,重要性采样的结果就会不好。 怎么避免它们相差太多呢?这就是PPO要做的事情。”
顺带,你可以对比下PPO算法的优化函数、和约束条件(别忘了,KL散度可以衡量两个分布之间相似程度)
其中, KL奖励系数 控制 KL 惩罚
控制 KL 惩罚 - 第三部分是加在最后边的偏置项,其中,
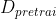 是预训练分布,预训练损失系数
是预训练分布,预训练损失系数 控制预训练梯度的强度,且
控制预训练梯度的强度,且 设置为0则称为PPO模型,否则称为PPO-ptx模型
设置为0则称为PPO模型,否则称为PPO-ptx模型
之所以加最后的这个偏置项,是防止ChatGPT在RL的训练过程中过渡优化,从而避免过于放飞自我,通过某种刁钻的方式取悦人类,而不是老老实实地根据人类的问题给出正确答案
最终,迭代式的更新奖励模型RM和策略模型SFT,让奖励模型对模型输出质量的刻画愈加精确,使得输出文本变得越来越符合人的认知
3.2 instructGPT:如何基于RLHF运用到多轮对话场景中
既然RLHF能很好地解决RL甚至IL的一些问题,也在InstructGPT中取得了很好的效果。那么,是否可以顺理成章地将之迁移到多轮对话场景中呢?或者说,ChatGPT是如何将这一套框架应用到多轮对话场景中的?
无限风光在险峰,故继续攀登,继续深入。
我们可以从强化学习的假设出发去理解这个问题。事实上,以PPO为代表的强化学习模型,基于马尔可夫性的假设。简单理解马尔科夫性就是,它将来的状态只取决于现在,与过去无关。也就是说,马尔可夫性有一个很重要的特点:无记忆性。
然而,在多轮人机对话场景中,模型却应该具备部分可观测马尔可夫性,即要求语言模型有“记忆性”。毕竟在多轮对话场景里,存在某一轮对话中的代词指向上一轮对话中的某个人或物的可能,假如模型不具备记忆性,那就无法很好地处理这种问题。显然,强化学习的假设与多轮对话场景的相背,不做一些优化的话很难直接应用。
那么进一步的问题来了,InstructGPT/ChatGPT是如何做优化的呢?
- 这里我们先从自然语言任务中最基本的语言模型简单说起。一个语言模型大概是说,当你给定前面的若干个词后,它会给你下一个词;而当你有了下一个词后,它会再给你接一个词,以此递推。
- 这就好比我们使用手机输入法,你打出一些词句后,输入法会提供若干个候选词——这里的手机输入法其实就是一个语言模型。那么我们如何利用这个最基本的语言模型来建模多轮对话问题呢?
- 实际上,我们向ChatGPT提出的问题,可以看成一句话,或者说是下图的输入
 。然后我们可以将ChatGPT给出的答案,抽象成下图的输出
。然后我们可以将ChatGPT给出的答案,抽象成下图的输出 。而ChatGPT这类语言模型,提供了若干个类似手机输入法的“候选句”,每个候选句对应的概率不一。所谓的语言模型的训练,其实就是让模型调整候选句对应的概率,使我们人类希望输出的候选句的概率尽可能大,而不希望输出的概率尽可能小。
。而ChatGPT这类语言模型,提供了若干个类似手机输入法的“候选句”,每个候选句对应的概率不一。所谓的语言模型的训练,其实就是让模型调整候选句对应的概率,使我们人类希望输出的候选句的概率尽可能大,而不希望输出的概率尽可能小。
那么这个语言模型和强化学习又有什么样的联系呢?在强化学习中,我们有智能体/模型(Agent)和环境(Environment)交互这样的范式。但是在ChatGPT所使用的训练方式中,环境从某种意义上说被直接被奖励模型RM取代了,如下图
- 图中的状态State是之前提到的输入语句
 ,而当智能体拿到一个
,而当智能体拿到一个 ,它给出的动作action其实是下一个单词
,它给出的动作action其实是下一个单词 。注意,GPT确实可以输出一整句话
。注意,GPT确实可以输出一整句话 ,但其实要完成这个最终的输出,需要做若干次如图所示的action。
,但其实要完成这个最终的输出,需要做若干次如图所示的action。 - 当环境(或RM)接收到它给出的单词
 后,会把这个单词放到已有的单词序列
后,会把这个单词放到已有的单词序列 末尾,然后再把这个新的单词序列还给智能体,之后依次类推
末尾,然后再把这个新的单词序列还给智能体,之后依次类推 - 打个比方,这里的智能体就是手机输入法,而环境就是使用输入法的用户。用户所做的事情,就是当输入法给出一系列候选词后,基于某种偏好选择某个词,然后让手机输入法再去猜下一个词,直到输入法把整个句子猜出来为止
这里我们明白了在语言模型场景下,强化学习的状态和动作对应什么,那么奖励Reward呢?由于上文已经分析过instructGPT的目标函数了,这里就不再赘述,直接上图:
至此,还有一个细节问题,即这个奖赏函数是对整个输入语句![]() 和整个输出语句
和整个输出语句![]() 而言的,而我们又在之前讨论过,智能体是根据一个一个词来去拼凑出整个回答的。图中的奖赏函数只能给出完整回答的奖赏,那么在智能体生成回答的过程中,每个动作action给出的词
而言的,而我们又在之前讨论过,智能体是根据一个一个词来去拼凑出整个回答的。图中的奖赏函数只能给出完整回答的奖赏,那么在智能体生成回答的过程中,每个动作action给出的词![]() 对应的奖赏是什么呢?
对应的奖赏是什么呢?
这个细节在InstructGPT中并没有给出。幸运的是,OpenAI团队2020年的另一篇论文《Learning from summarize from Human feedback》中的一个引脚标注给出了关于这个疑问的答案。作者说,奖赏模型只在最终生成回答之后才给出奖赏,在中间的过程中是不给出奖赏的。在这里作者没有使用回答一词,而是使用总结一词,因为它的任务是将一篇长文章进行归纳总结。
同时,还有一个意外收获,发现这篇论文里就已经提出了instructGPT/chatgpt类似的训练模式:1 根据人来标注数据微调监督模型,2 训练一个奖励函数,3 通过PPO优化原始监督模型的策略
顺着这位作者的思路,只有在ChatGPT输出了EOS token的时候,整个轨迹才结束(EOS token是自然语言处理中用来表示一段话结束的标志)。
最后再让我们回顾梳理下这个问题:RLHF是如何运用到ChatGPT中的多轮对话场景中的?
- 由于多轮对话要求语言模型有记忆性,因此无法直接使用强化学习。这里的矛盾具体体现在了奖赏函数中:ChatGPT的奖赏函数是针对GPT的一整个输入语句
 和一整个输出语句
和一整个输出语句 而言的;
而言的; - 而ChatGPT的语言模型在强化学习的训练策略中,每个action其实输出的是一个个词语。因此,OpenAI的团队可能是采取不对序列的中间生成给予reward的方式解决上文提到的矛盾,而这种解决方式十分接近SeqGAN的思路
问题又来了,什么是SeqGAN(Sequence Generative Adversarial Nets with Policy Gradient)呢?
第四部分 扩展:SeqGAN——NLP下对抗思想与RL的碰撞
4.1 SeqGAN模型:改进GAN只能处理图像数据
4.1.1 从GAN到SeqGAN:把GAN用到NLP领域里
非连续性序列生成,比如说文本生成(注意,图像和文本的核心区别在于图像的Pixel表示是连续的,而文本是由离散的token组成),为什么单纯的使用GAN没有取得很好的效果呢?主要的屏障有两点:
- 在GAN中,Generator 用于生成文本的,而Discriminator则判别文本是真实的还是生成的
一开始,Generator通过随机抽样作为开始,然后根据模型的参数进行确定性的转化。通过generative model G的输出,discriminative model D计算的损失值,根据得到的损失梯度(即把生成文本与真实文本之间的差异转化为loss)去指导generative model G做轻微改变,从而使G产生更加真实的数据
但在文本生成任务中,G通常使用的是LSTM,那么G传递给D的是一堆离散值序列,即每一个LSTM单元的输出经过softmax之后再取argmax,或者基于概率采样得到一个具体的单词,这使得梯度下降很难处理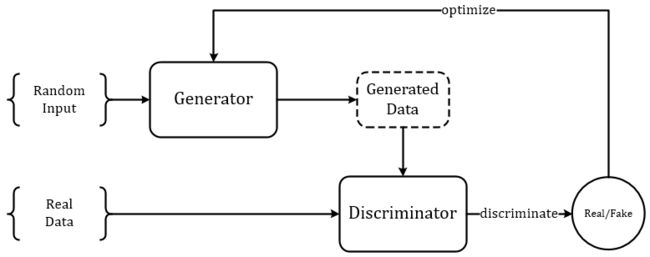
说白了,就是在处理离散数据时,判别器难以使用SGD直接将梯度信息传递给生成器,从而G和D都无法进行更新 - GAN只能评估出整个生成序列的score/loss,不能够细化到去评估当前生成token的好坏和对后面生成的影响
说白了,就是判别器只能针对于完整的序列数据给出判别结果
如果有办法解决上面的两个问题,便可以尝试将GAN用于NLP中。SeqGAN就提供了一种很巧妙的思路来解决这两个问题:
- 再回想一下Policy Gradient的基本思想,即通过reward作为反馈,增加得到reward大的动作出现的概率,减小reward小的动作出现的概率,如果我们有了reward,就可以进行梯度训练,从而更新参数
相当于如果GAN结合Policy Gradient后,当G产生一个单词时,如果能够得到一个反馈的Reward,就能通过这个reward来更新G的参数,而不再需要依赖于D的反向传播来更新参数,因此较好的解决了上面所说的第一个屏障
换言之,无法直接使用常规的随机梯度下降进行参数的更新,那就使用强化学习中的策略梯度(policy gradient)
进一步讲,如果我们把Generator 看成是一个 Agent,他在每一 time step 上生成的 word token 作为 action,此前生成的所有 tokens 作为 state,我们就可以设计一个 reward function 来指导 Generator 生成更真实的句子。
因为 Discriminator 输出是真实句子的概率 0-1,直接拿来作为 reward,于是就有了下面的式子:
但是对于生成了一半的句子怎么评估其真实性呢?用蒙特卡洛(蒙特卡洛就是随机采样)搜索在一个 Generator 的拷贝上(为了避免搜索过程引入对梯度的影响)补全句子,然后再交给 Discriminator 评估。于是,完成的 Q function 如下: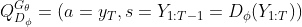
- 对于第二个屏障,当产生一个单词时,我们可以使用蒙塔卡罗树搜索(AlphoGo也运用了此方法)立即评估当前单词的好坏,而不需要等到整个序列结束再来评价这个单词的好坏
换言之,既然判别器无法直接处理部分生成的序列,那就使用蒙特卡洛搜索(Monte Carlo Search)来将已生成的序列补成完整的序列再给出得分
因此,强化学习和对抗思想的结合,理论上可以解决非连续序列生成的问题,而SeqGAN模型,正是这两种思想碰撞而产生的可用于文本序列生成的模型。
4.1.2 SeqGAN在对话聊天中的应用
其实早就有人将RL应用于对话生成的训练当中,因为对话生成任务本身非常符合RL的运行机理(让人类满意,拿奖励)。假设根据输入句子![]() ,返回的回答
,返回的回答 ![]() 从人类得到的奖励记为
从人类得到的奖励记为 ![]() ,而Encoder-Decoder对话模型服从的参数被统一记为
,而Encoder-Decoder对话模型服从的参数被统一记为![]() ,则基于RL的目标函数说白了就是最大化生成对话的期望奖励,其中
,则基于RL的目标函数说白了就是最大化生成对话的期望奖励,其中 ![]() 表示在参数
表示在参数 ![]() 下,一组对话
下,一组对话![]() 出现的概率。
出现的概率。
既然是一个最优化的问题,很直接地便想到使用基于梯度的优化方法解决。当然,在强化学习中,我们要得到的是最优策略![]() ,继而我们可以用策略梯度算法解决。
,继而我们可以用策略梯度算法解决。
具体做法和2.3.1节推导策略梯度计算的公式类似,再贴一下
引用参考文献44的推导过程,如下
所以,当我们把等式 argmaxθ(⋅) 中的右边项单独记为
,它表示对话模型找到最优参数时所得到的奖励期望。实际中,某句话的应答有N种可能性,则每组对话
出现的概率可视为服从均匀分布,故还可以进行如下变形:
在优化过程中,对话模型的权重
更新如下,
为所获奖励的变化梯度
借助复合函数的求导法则,继续推导奖励的变化梯度,
这样一来,梯度优化的重心就转化到了生成对话的概率上来,也就是说,通过对参数
进行更新,奖励会使模型趋于将优质对话的出现概率提高,而惩罚则会让模型趋于将劣质对话的出现概率降低。
SeqGAN的提出为GAN用于对话生成(Chatbot)完成了重要的铺垫,同样起到铺垫作用的还有另外一个GAN在图像生成领域的神奇应用——Conditional GAN[18~19],有条件的GAN,顾名思义就是根据一定的条件生成一定的东西,该工作根据输入的文字描述作为条件,生成对应的图像,比如:
对话生成可以理解为同样的模式,上一句对话作为条件,下一句应答则为要生成的数据,唯一的不同是需要生成离散的文本数据,而这个问题,SeqGAN已经帮忙解决了。权且称之为:Conditional SeqGAN。Conditional SeqGAN中的优化梯度可写成:
不难看出,此式子与上面的变化梯度仅一字之差,只是把“打分器”给出的奖励得分![]() 换成了鉴别器认为生成对话来自真人的概率得分
换成了鉴别器认为生成对话来自真人的概率得分![]() :
:
- 在原本的强化学习对话生成中,虽然采用了AI互相对话,并设定了 jugle 进行打分,但这个 jugle 是预训练好的,在对话模型的训练过程当中将不再发生变化;
- RL + GAN 的文本生成乃至对话模型则不同,鉴别器D与生成器G的训练更新将交替进行,此消彼长,故而给出奖励得分的鉴别器D在这里是动态的(dynamic)
总之,RL+ GAN 利用强化学习中的Reward机制以及 Policy Gradient 等技术,巧妙地避开了GAN面对离散数据时梯度无法BP的难题,在使用强化学习的方法训练生成器G的间隙,又采用对抗学习的原版方法训练判别器D。 在Conditional SeqGAN对话模型的一些精选结果中,RL+ GAN 训练得到的生成器时常能返回一些类似真人的逼真回答。
此外,值得一提的是,我们所熟知的Actor-Critic是不是也是一种更广义上的GAN呢?
4.2 逆强化学习就是GAN技术:ChatGPT = Transformer + SeqGAN
至此,我们总结下
- 我们可以将ChatGPT这种聊天机器人理解为模仿学习,在聊天机器人里面我们会收集到很多人交互对话的记录,这些就是所谓专家的示范
对于ChatGPT而言,什么可以被称为一个最好的奖励函数呢?最后我们学习出来的奖励函数应该是人类标注知识和ChatGPT本身在这个奖励函数上都会得到一样高的分数,最终的奖励函数无法分辨出谁应该会得到比较高的分数,也就是你不知道你在对话的背后到底是真实的人,还是只是机器ChatGPT了。 - SeqGAN对应逆强化学习,我们把逆强化学习的技术放在句子生成、聊天机器人里面,其实就是SeqGAN与它的种种变形
这里我们可以梳理下RLHF和GPT的本质关系。实际上,这里使用RLHF就是为了解决我们无法对一个离散的训练进行求导的问题。而使用强化学习来解决这个问题也不是ChatGPT的独创:早在2016年SeqGAN的作者就已经使用了这样的方法了。因此我们可以从问题本质的角度去这么理解ChatGPT:它就是把Transformer和“SeqGAN”结合在一起。
从问题本质上看,ChatGPT与之前的工作的最大不同,就体现在它使用了类似SeqGAN的方式进行微调:先通过基于人类偏好定义奖励函数,再基于奖励函数通过PPO持续优化。
参考文献与推荐阅读
- BERT通俗笔记:从Word2Vec/Transformer逐步理解到BERT,July
- 《预训练语言模型》,电子工业出版
- GPT,GPT-2,GPT-3 论文精读
- GPT到GPT2、GPT3各自对应的原始论文,可以在这里找到:https://beta.openai.com/docs/model-index-for-researchers
- prompt提示学习(一)简要介绍
- CMU刘鹏飞:近代自然语言处理技术发展的“第四范式”
- 大模型prompt Turing技术上,这是针对这次分享的解读
- NLP小样本学习:如何用20条数据完成文本分类,此外,小样本学习也是七月NLP高级班上重点讲的技术之一,最新一期NLP11则加入了ChatGPT背后原理的解析
- GPT-3.5 + ChatGPT: An illustrated overview - Life Architect
- 强化学习入门这一篇就够了
- 《白话强化学习与Pytorch》,此书让我1.6日起正式开启RL之旅,没看此书之前,很多RL资料都不好看懂
- 《Eazy RL强化学习教程》,基于台大李宏毅和UCLA周博磊等人的RL公开课所编著,其GitHub、其在线阅读地址
- 台大李宏毅RL公开课,这是其:视频/PPT/PDF下载地址
- UCLA周博磊RL公开课,这是其:GitHub地址
- 关于Q-leaning的几篇文章:1 如何用简单例子讲解 Q - learning 的具体过程? 2 莫烦:什么是 Q-Learning
- AlphaGo作者之一David Silver主讲的增强学习笔记1、笔记2,另附课件地址
-
huggingface的两篇RL教程:An Introduction to Deep Reinforcement Learning、GitHub:The Hugging Face Deep Reinforcement Learning Course
- TRPO原始论文:Trust Region Policy Optimization
- PPO原始论文:Proximal Policy Optimization Algorithms
- PPO算法解读(英文2篇):解读1 RL — Proximal Policy Optimization (PPO) Explained、解读2 Proximal Policy Optimization (PPO)
- PPO算法解读(中文3篇):Easy RL上关于PPO的详解、详解近端策略优化、详解深度强化学习 PPO算法
- PPO算法实现:https://github.com/lvwerra/trl
- 如何选择深度强化学习算法?MuZero/SAC/PPO/TD3/DDPG/DQN/等
- Google搜索:instructGPT如何基于PPO算法进行训练,出来的一系列文章
- InstructGPT原始论文(确实有68页,^_^):Training language models to follow instructions with human feedback,这是翻译版之一,这是翻译之二
- InstructGPT 论文精读,来自动手学深度学习一书作者李沐的解读
- ChatGPT: Optimizing Language Models for Dialogue,OpenAI关于ChatGPT的官方发布页面
- ChatGPT会取代搜索引擎吗,张俊林
- Illustrating Reinforcement Learning from Human Feedback (RLHF),另这是中文翻译版之一
- OpenAI联合DeepMind发布全新研究:根据人类反馈进行强化学习
- 基于人类偏好的深度强化学习(Deep reinforcement learning from human preferences),这是翻译版之一,这是解读之一
- 《Learning from summarize from Human feedback》,OpenAI团队2020年的文章,说明2020年便已经开始研究RLHF了
- HuggingFace的视频分享:RL from Human Feedback- From Zero to chatGPT
- OpenAI's InstructGPT: Aligning Language Models with Human Intent
- 不忽悠的ChatGPT,作者Ben
- 别光顾着玩,让我来告诉你ChatGPT的原理,来自B站UP主弗兰克甜
- 浅析ChatGPT的原理及应用
- 如何通俗理解隐马尔可夫模型HMM?
- HMM学习最佳范例
- GAN之父在NIPS 2016上做的报告:两个竞争网络的对抗(含译文下载)
- AAAI 2017 《SeqGAN: Sequence Generative Adversarial Nets with Policy Gradient》
- SeqGAN —— GAN + RL +NLP
- 对抗思想与强化学习的碰撞-SeqGAN模型原理和代码解析
- Role of RL in Text Generation by GAN(强化学习在生成对抗网络文本生成中扮演的角色)
- 抱抱脸:ChatGPT背后的算法——RLHF
后记:下一篇笔记RL极简入门
事实上,可能很多朋友也已经意识到,本文的前大部分内容里,GPT-N理解起来相对轻松,而instructGPT/ChatGPT的整体架构思想也不算复杂,但其中涉及到的强化学习部分则让想深挖细节的初学者变得立马吃力起来(除非你已“入一定门”,或者你有课程/老师可以不断问),看似就两个概念,一个RLHF,一个PPO算法,但要真正把这两个概念讲清楚、讲透彻则没那么容易了,特别是PPO算法。
所以1.6日决定只是想写个ChatGPT通俗导论,但为了讲清楚其中的PPO算法,更考虑到ChatGPT笔记之后,再下一篇是强化学习极简入门,故中途花了大半时间去从头彻底搞懂RL,最终把网上关于RL的大部分中英文资料都翻遍之外(详见参考文献与推荐阅读),还专门买了这几本强化学习中文书以系统学习
- 第1本(1.7下午-1.8日),《白话强化学习与pytorch》,偏通俗,对初学者最友好,可以最快最短时间内入门RL,缺点是对部分前沿/细节比如PPO算法阐述不足,毕竟19年出版的了
- 第2本(1.9-1.10凌晨),《Eazy RL强化学习教程》,基于台大李宏毅等人的公开课,对于初学入门不错的,入门之后可以看下面的第4~6本
- 第3本,《深度强化学习图解》,偏图表示例
- 第4本,《动手学强化学习》,张伟楠等人著,偏代码实现
- 第5本,《深度强化学习》,王树森等人著,偏原理讲解,此书对于已对RL有一定了解的是不错的选择,对于尚未了解RL的则如果能再通俗易懂些会更好
- 第6本,《强化学习2》,权威度最高但通俗性不足,当然 也看人,没入门之前你会觉得此书晦涩,入门之后你会发现经典还是经典、不可替代,另书之外可配套七月的强化学习2带读课
总之,RL里面的概念和公式很多(相比ML/DL,RL因为想要机器/程序具备更高、更好的自主决策能力),而绝大部分的资料:没有站在初学者的角度去通俗易懂化、没有把概念形象具体化、没有把公式拆解举例化(如果逐一做到了这三点,何愁写不出通俗易懂的文章/书籍/课程)。
以下是本文自1.15发布初稿之后的修改记录:
- 1.16,修正第一部分GPT-N几个笔误,且考虑到不排除会有比初级更初级的初学者阅读本文,补充第二部分2.3.3节部分公式的拆解细节,微调第四部分关于SeqGAN的部分公式表述
- 1.17,先后修正了2.3节重要性采样与重要性权重的部分不准确的描述、修正个别公式的笔误,以及补充2.4.2中关于PPO-clip的细节阐述、优化第四部分的相关描述
- 1.18,








![\mathbb{E}_{x \sim p}[f(x)] \approx \frac{1}{N} \sum_{i=1}^N f(x^i)](http://img.e-com-net.com/image/info8/f1596b9fd65c4e679818387e3fccc861.gif)