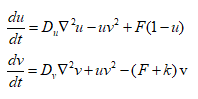使用python实现图灵斑图（以Gray-Scott为例）

这几天在学习斑图动力学，对于一个计算机菜鸡来说搞这个难度真的是颇大哦！看概念和公式真的是一遍又一遍，难受≧ ﹏ ≦。。。

哈哈，废话不多说了！对于matlab，我猜可能好多程序员都是抵触的吧（反正我是这样）！但是斑图的实现基本都是matlab来实现的，找了半天都没找到python版的！本来想着从程度角度来理解一下斑图（可能这就是程序员的思维吧，哈哈！），这下没得办法了，只能自己来喽！

这回仿照了这边文章来写https://blog.csdn.net/weixin_30278943/article/details/112067158?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522161551707416780265433572%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=161551707416780265433572&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduend~default-1-112067158.first_rank_v2_pc_rank_v29&utm_term=%E5%9B%BE%E7%81%B5%E6%96%91%E5%9B%BEmatlab%E4%BB%A3%E7%A0%81

（突然发现自己写一遍大概可以了解斑图动力学的一点皮毛了哦！）

基础知识

反应扩撒方程的一般形式：

其中 U和V表示两种反应物，Du和Dv表示扩散系数，f(U,V)和g(U,V)表示两种物质的生成率，图灵认为这两项是二次多项式

Gray-Scott模型：

化学反应方程：

反应扩散方程：

上述方程中：

源代码：

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
File Name:    Gray-Scott.py
Author:       Wang_Huiyu
Email:        [email protected]
Time:         2021/3/12 10:52
"""


import matplotlib.pyplot as plt
import numpy as np
import random

def my_laplacian(In):
    Out = -1.0 * In + 0.20*(np.roll(In,1,axis=1)+np.roll(In,-1,axis=1)+np.roll(In,1,axis=0)+np.roll(In,-1,axis=0) ) + \
          0.05*(np.roll(np.roll(In,1,axis=0),1,axis=1)+np.roll(np.roll(In,-1,axis=0),1,axis=1)+np.roll(np.roll(In,1,axis=0),-1,axis=1)+np.roll(np.roll(In,-1,axis=0),-1,axis=1))
    return Out


def initial_conditions(n):
    A = np.ones((n,n),dtype=float)
    B = np.zeros((n,n),dtype=float)
    t=0

    for i in range(50, 60):
        for j in range(50, 70):
            B[i, j] = 1

    for i in range(60, 80):
        for j in range(70, 80):
            B[i, j] = 1

    return t,A,B


if __name__=="__main__":
    f = 0.055       #进料率
    k = 0.062       #去除率
    da = 1.0          #U的扩散率
    db = 0.5        #V的扩散率
    width = 128     #网格大小
    dt = 0.25       #每进行一需要0.25秒
    stoptime = 10000.0 #一共有5000秒模拟时间


    t,A,B = initial_conditions(width)

    nframes = 1

    while t < stoptime:
        anew = A + (da*my_laplacian(A) - A*(B*B) + f*(1-A))*dt
        bnew = B + (db*my_laplacian(B) + A*(B*B) - (k+f)*B)*dt

        A=anew
        B=bnew
        t=t+dt
        nframes=nframes+1

    fig, ax0 = plt.subplots()
    f = ax0.pcolor(B)
    fig.colorbar(f, ax=ax0)

    plt.show()

A对应与反应物U，B对应于反应物V

函数my_laplacian(In)

应该就是表示传说中的拉普拉斯算符！（这个真的是醉了，百度了半天也没有搞懂公式中的大名鼎鼎的拉普拉斯算符！这里我的理解是就类似一个交警，可以帮你指挥反应物如何扩散到附近位置的这么一个东西！哈哈哈，可能不准确哦，以后回来再改！）

我们可以想象一下计算机画图的网格是上下和左右连城一体的！就比如说我靠近左边界的反应物可以直接扩撒到右边界，上边界的反应物可以直接扩撒到下边界！

函数initial_conditions(n):

初始化反应物浓度！

这里表示反应物U是均匀分布的，即A是全1的矩阵；反应物V是在两块长方形区域内均匀分布，具体就是B中元素为1的区域，其他区域没有反应物

对应扩散方程的代码：

 while t < stoptime:
        anew = A + (da*my_laplacian(A) - A*(B*B) + f*(1-A))*dt
        bnew = B + (db*my_laplacian(B) + A*(B*B) - (k+f)*B)*dt

哇！这里原文上使用了matlab的点乘幂，结果我写成了B*2，结果怎么都结果不对，难定哦！

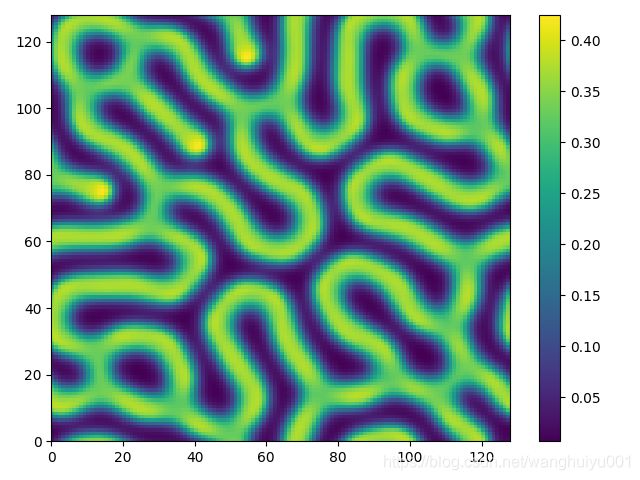
生成的斑图：

stoptime=1000 时的斑图