机器学习(八):CS229ML课程笔记(4)——生成学习,高斯判别分析,朴素贝叶斯
到目前为止,我们主要学习了学习算法模型:![]() ,在给定以θ为参数的x时y的分布。比如说逻辑回归模型:
,在给定以θ为参数的x时y的分布。比如说逻辑回归模型:![]() ,g是sigmoid function。今天我们学的是一种不同的学习算法——生成学习算法。
,g是sigmoid function。今天我们学的是一种不同的学习算法——生成学习算法。
Part4 生成模型、高斯判别分析、朴素贝叶斯
1.判别学习算法和生成学习算法
① 判别学习算法(discriminative learning algorithm):训练出一个总模型,把新来的样本放到这个总模型中,直接根据总模型输出结果对新样本进行判断。
比如前面的二类分类,在解空间寻找一条直线把样例分开,对于新样本直接判断它在直线的哪边即可。
(P(Y|X)是条件概率,在已知X发生概率下,Y发生的概率.P(Y|X)=P(A和B)/P(A)
P(X,Y)说明该事件与两个因素有关)
形式化:判别学习方法是对后验概率P(y|x)进行建模或者直接学习输入空间到输出空间的映射关系,x表示的是输入样例的特征,y表示输入样例的分类标记。
② 生成学习算法(generate learning algorithm):对两个类别分别进行建模,用新的样例去匹配两个模型,匹配度高的作为新样例的类别。
比如先训练出一个良性肿瘤的模型,再训练出一个恶性肿瘤的模型。把新来的样本分别放到良性肿瘤的模型和恶性肿瘤的模型里,看它生成的概率分别是多少。选择生成的概率比较大的一个模型,就即为新样本的类别。
形式化:生成学习方法是对P(x|y)(条件概率)和P(y)(先验概率)进行建模,然后按照贝叶斯法则求出后验概率P(y|x):![]()
使得后验概率最大的类别y即是新样例的预测值:
(先建立的两个P(yi|x)求概率的模型,因为在对比模型哪个概率大的过程中,x样本是一样的,yi是两个类别。上述的p(x)先验概率是一样的所以才可以那样简化)
2. 高斯判别分析:(Gaussian Discriminant analysis)
GDA不是判别算法而是生成算法,在了解这个算法之前我们要先熟悉一下多元正态分布。
2.1 多元正态分布:(the multivariable normal distribution)
多元正态分布也叫多元高斯分布,是正态分布在多维变量的扩展,它的参数是一个均值向量(mean vector)![]() 和一个协方差矩阵(covariance matrix)
和一个协方差矩阵(covariance matrix)![]() ,其中n表示多维变量的向量长度,
,其中n表示多维变量的向量长度,![]() 是对称正定矩阵。多元正态分布也可以写成
是对称正定矩阵。多元正态分布也可以写成![]() ,它的密度函数可以表示为:
,它的密度函数可以表示为:
其中![]() 表示矩阵的绝对值。
表示矩阵的绝对值。
对于一个服从多元正态分布的随机变量x,均值可以表示为:
一个向量值随机变量Z的协方差被定义为:
对于一个服从多元正态分布的随机变量x,协方差可以表示为:
![]()
下面来看看二元高斯分布的概率密度函数的样子
(a) (b) (c)
其中(a)表示的是均值为0(2×1矩阵),协方差矩阵为单位矩阵的情况![]() (2×2矩阵),这也被叫做标准正态分布;(b)表示的是均值为0(2×1矩阵),协方差矩阵
(2×2矩阵),这也被叫做标准正态分布;(b)表示的是均值为0(2×1矩阵),协方差矩阵![]() ;(c)表示的是均值为0(2×1矩阵),协方差矩阵
;(c)表示的是均值为0(2×1矩阵),协方差矩阵![]() 我们可以发现,当协方差∑越小,高斯分布越“peaked”(越陡峭),协方差∑越大,分布越 “spread-out”(扁平的)
我们可以发现,当协方差∑越小,高斯分布越“peaked”(越陡峭),协方差∑越大,分布越 “spread-out”(扁平的)
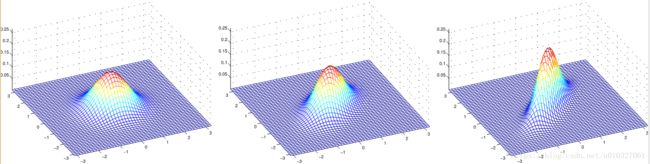
2.1.1 协方差矩阵∑进行改变对二元高斯分布的影响(决定投影椭圆的朝向和大小):
(a) (b) (c)
其对应的协方差分别是:
(a)是我们熟悉的标准正态分布,当我们增加协方差矩阵的非对角线数值的大小时,我们可以看到分布在x1=x2的方向的改变。(相关度越高)
我们再看一个例子,方便我们的理解:
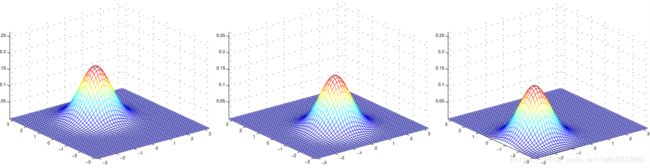
2.1.2 均值改变对二元高斯分布的影响(决定投影中心位置)
对应的均值:
2.2 高斯判别分析模型:(Gaussian Discriminant analysis model)
GDA解决的是连续型随机变量的分类问题。也就是训练集的特征值x是随机连续值。
(什么是连续型随机变量呢?举两个例子:
公交车15分钟一趟,某人的等车时间x是区间[0,15)中的一个数,x是连续型随机变量,可以取小数甚至无理数。 再比如说,抛20枚硬币,硬币朝上的数量x只能取0~20之间的整数,不能取0.1,根号3这样的小数或者无理数,所以这里的x是离散型随机变量。
概率论基础知识:
概率分布函数为:F(x);概率密度函数为:f(x);二者的关系为:f(x) = dF(x)/dx,即:密度函数f 为分布函数 F 的一阶导数。或者分布函数为密度函数的积分。
理解:
只有连续型随机变量的概率密度函数可以积分,得到分布函数,这样才能用多元高斯分布对p(x∣y)建模,进而使用高斯判别式。)
进入正题:
假设p(x|y)满足多元正态分布,即:
则其概率密度函数为:
而这些分布里面一共有ϕ,μ0,μ1,Σ4个参数,φ是训练样本中标签为1的训练样本所占的比例。注意μ0,μ1是不同模型的均值矩阵,表示在不同的结果模型下,特征均值不同,但我们假设协方差相同。反映在图上就是不同模型中心位置不同,但形状相同。这样就可以用直线来进行分隔判别。
之后我们得到数据集的最大似然函数的对数(m是样本数),求的是“log联合概率(joint likelihood)”:
我们再次回顾一下逻辑回归:
来自:机器学习(六):CS229ML课程笔记(2)——逻辑回归
逻辑回归求的是条件概率(conditional likelihood)。
再回到联合概率:
根据最大似然估计(对L函数对相应的参数求导=0解求各参数的值)得到使L函数最大时候各个参数:
(1{⋅}表示逻辑判断,真就输出1 ,反之输出0。)
φ是训练样本中标签为1的训练样本所占的比例。
μ0的分母表示训练集合中标签为0的样本数目,分子表示只有标签样本数为0,分括号才输出为1,再乘以x(i)相加,总体分子就表示对标签为0的所有样本的x(i)之和。样本标签为0的x(i)之和除以总样本数,也就是x(i)的平均值就是u0.
μ1就不难理解了。
predict:
在找到这些参数之后我们现在要开始做预测了,当得到一个新的x:
(再次温习生成学习模型的原理( ):这里有先验概率p(y)(因为是伯努利分布,所以y的取值是0或者1),具体猜测的似然性p(x∣y=0)与p(x∣y=1),在生成模型中,会对p(y=n)p(x∣y=n)进行计算,分别得到输入x被分类为0与被分类为1的概率,然后再对这两个概率进行比较,取较大的那个最为分类结果。)
):这里有先验概率p(y)(因为是伯努利分布,所以y的取值是0或者1),具体猜测的似然性p(x∣y=0)与p(x∣y=1),在生成模型中,会对p(y=n)p(x∣y=n)进行计算,分别得到输入x被分类为0与被分类为1的概率,然后再对这两个概率进行比较,取较大的那个最为分类结果。)
(argmax表示使后面式子求最大的时候y的值)
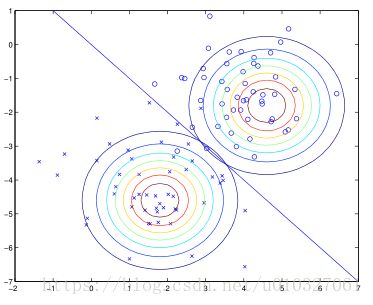
最后用图像展示分类结果:
在直线所示的部分,P(y=1|x)=P(y=0|x)=0.5
下边的大圆表示"x"正样本的高斯分布p(x|y=1),上面的大圆表示“o”样本的高斯分布p(x|y=0).用高斯判别分析得到了中间的蓝线。
2.3 关于GDA和逻辑回归的讨论
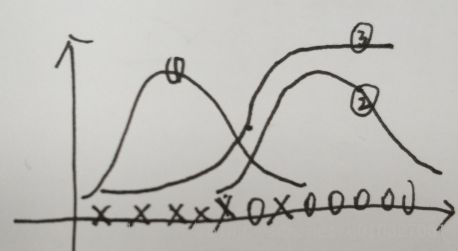
上面是吴恩达老师在公开课画出的图(我用手画的,有点丑):
其中①是“x”样本的高斯分布(P(x|y=0),②是“o”样本的高斯分布(P(x|y=1),③是我们画出的P(y=1|x)的曲线。(根据P(y=1|x)=(P(x|y=1)*P(y=1))/P(x)估计,P(x)=(P(x|y=0)*P(y=0)+(P(x|y=1)*P(y=1))
也就是在使用GDA模型的时候,其中P(x|y=1)属于高斯分布,当你用此计算P(y=1|x),发现这和逻辑回归的sigomid函数长的很相似,但是无论位置和陡峭程度都不完全一样。
逻辑回归和GDA在训练相同的数据集的时候会得到两种不同的决策边界,那么怎么样来进行选择模型呢?
上面提到如果p(x|y)是一个多维的高斯分布,那么p(y|x)可以推出一个logistic函数;反之则不正确,p(y|x)是一个logistic函数并不能推出p(x|y)服从高斯分布.这说明GDA比logistic回归做了更强的模型假设(高斯),而逻辑回归做出更少的假设构建模型(可能是高斯也可能是泊松),许多不同的假设能够推出logistic函数的形式,因此它在在建模方面有鲁棒性。但如果p(x|y)真的服从或者趋近于服从高斯分布,则GDA比logistic回归效率高,而且使用的样本数量很少效果也很好。
3. 朴素贝叶斯(Naive Bayes,NB)
在GDA中,特征向量x是连续的实数向量,NB针对的是特征向量x是离散值的问题.(对于特征是连续值的情况,我们也可以采用分段的方法来将连续值转化为离散值).
NB的标准应用也是最常见的的应用就是文本分类问题,邮件分类是文本分类(text classification )的一种应用。我们沿用对垃圾邮件进行分类的例子,区分邮件是不是垃圾邮件。
3.1 确定特征向量x(feature vector):
在此模型下,向量x是一本词典,它的每一个元素都是一个单词,对于词典中的每一个词都有一个向量中对应的元素xi作为标记,xi的取值为0或者1,1表示邮件中这个词出现过,0表示这个词没有出现过。(向量空间模型VSM,vector space model)
比如:
x的长度表示词典中所有词的总共个数,上面的x表示一封邮件中出现了a和buy这两个词。
3.2 构建判别模型 p(x|y)(多元伯努利事件模型(NB-MBEM,向量x表示一本词典))
假设字典中有50000个词,![]() (50000维的0和1组成的向量)。如果采用多项式建模,将会有
(50000维的0和1组成的向量)。如果采用多项式建模,将会有![]() 种结果,
种结果,![]() -1维的参数向量,这样明显参数过多。因此NB算法做了其他的假设。
-1维的参数向量,这样明显参数过多。因此NB算法做了其他的假设。
假设x的特征是条件独立的(![]() ),这个假设称为朴素贝叶斯假设(Naive Bayes (NB) assumption),这个算法就称为朴素贝叶斯分类(Naive Bayes classifier).
),这个假设称为朴素贝叶斯假设(Naive Bayes (NB) assumption),这个算法就称为朴素贝叶斯分类(Naive Bayes classifier).
(条件独立和独立不同,参考:https://blog.csdn.net/lanchunhui/article/details/53696550
无条件的独立是十分稀少的,因为大部分情况下,事件之间都是互相影响的。然而,通常这种影响又往往依赖于其他变量而不是直接产生。所以出现了条件独立。
条件独立:![]() 。X与 Y 的依赖关系借由 Z 产生。)
。X与 Y 的依赖关系借由 Z 产生。)
如果有一封垃圾邮件(y=1),在邮件中2087这个位置出现buy这个词和在它对39831这个位置是否出现price这个词都没有影响,我们可以这样表达p(x2087|y) = p(x2087|y, x39831),这个和x2087 and x39831 相互独立不同,如果相互独立,则可以写为p(x2087) = p(x2087|x39831),我们这里假设的是在给定y的情况下,x2087 and x39831 独立。
所以,在给定y的类别之后,特征向量的各个分量是相互独立的。因此:
第一个等号用到的是常用的概率的性质 链式法则,第二个等式用到的是朴素贝叶斯假设,朴素贝叶斯假设是约束性很强的假设,虽然在理论上这样的假设是有点问题的,比如说你在一个邮件里看到了课程的名字,就有很大的可能看到导师或者助教的名字。但是虽然假设有一定的错误性,但是朴素贝叶斯算法对于分类仍旧是个很好的算法。
下面开始构建模型,模型参数为:
φi|y=1 = p(xi= 1|y = 1)
φi|y=0 = p(xi = 1|y = 0)
φy = p(y = 1)
对于训练集{(x(i) , y(i)); i =1, . . . , m},根据生成学习模型规则,联合似然函数(joint likelihood)为:
(求联合似然函数操作:https://blog.csdn.net/expleeve/article/details/50466602)
![]() 得到最大似然估计值:
得到最大似然估计值:
![]()
φj|y=1 的分子表示,遍历所有样本,寻找标签y=1也就是垃圾邮件中j词语出现的次数,分母表示训练集合中垃圾邮件的总数。总的式子就表示在垃圾邮件中j词语出现的概率。
同理,φj|y=0 表示在非垃圾邮件中j词语出现的概率。
φy表示垃圾邮件占所有样本样件总数的比例。
其中的![]() 表示“and”。
表示“and”。
拟合好所有的参数后,如果我们现在要对一个新的样本进行预测,特征为x,则有:
实际上只要比较分子就行了,分母对于y = 0和y = 1是一样的,这时只要比较p(y = 0|x)与p(y = 1|x)哪个大就可以确定邮件是否是垃圾邮件。
3.3拉普拉斯平滑(Laplace smoothing)
朴素贝叶斯模型可以在大部分情况下工作良好。但是该模型有一个缺点:对数据稀疏问题敏感。
比如在邮件分类中,普通学生要在NIPS(顶尖机器学习会议)发文章不是很容易,邮件中可能没有出现过,现在新来了一个邮件"NIPS call for papers",假设NIPS这个词在词典中的位置为35000,然而NIPS这个词从来没有在训练数据中出现过,这是第一次出现NIPS,于是算概率时:
![]()
由于NIPS从未在垃圾邮件和正常邮件中出现过,所以结果只能是0了。于是最后的后验概率:
![]()
对于这样的情况,我们可以采用拉普拉斯平滑,是假设每个特征值都出现过一次,对于未出现的特征,我们赋予一个小的值而不是0。具体平滑方法为:
假设离散随机变量取值为{1,2,···,k},原来的估计公式(某个结果出现的次数在总试验次数中的比例)为:
![]()
使用拉普拉斯平滑后,新的估计公式为:
![]()
即每个k值出现次数加1,分母总的加k,类似于NLP中的平滑,具体参考宗成庆老师的《统计自然语言处理》一书。
对于上述的朴素贝叶斯模型,参数计算公式改为:
![]()
example:
A队和别人打比赛,在过去的样本中,A和B打了两次,输了两次,A和C打了两次,输了两次,A和D打了一次,输了一次,问现在A和E打赢得概率:
如果不用拉普拉斯平滑算出来最后A和E打肯定输,但是是不合常理的。我们进行平滑后的计算:
P(y=1)= (赢的概率)/(总场数输+赢)
平滑就是假设已经输了一局赢了一局,所以目前:
P(y=1)= 0+1/5+1+1=1/7.
3.4 多项式事件模型(NB-MEM(multinomial event model),向量x表示一个邮件)
对 3.2 提到的NB-MBEM模型目前有很多的扩展。比如将每个分量多值化,即将P(x|y)由伯努利分布扩展到多项式分布;再比如将连续变量值离散化(分段表示)。
目前将介绍第一种,也就是将P(x|y)由伯努利分布扩展到多项式分布。这是与多元伯努利事件模型(NB-MBEM)有较大区别的NB模型,即多项式事件模型(multinomial event model,NB-MEM)。
首先,NB-MBEM中的特种向量x的每个分量代表词典中该索引上的词语在本文中是否出现过,取值范围为{0,1},特征向量的长度为词典的大小;而在NB-MEM中,特征向量x的每个分量的值使文本中处于该分量的位置的词语在词典中的索引,其取值范围是{1,2,....|V|}.|V|表示词典的大小,特征向量的长度为相应样例文本中词语的数目。
example:
NB-MBEM:一篇文档的特征向量可能如下所示,表示一封邮件中出现了a和buy这两个词:
NB-MEM:向量可能如下,表示这封邮件的“the”在词典中的43000位置,“a”在词典中第一个位置:
所以,在此让i表示邮件中的第i个词,xi表示这个词在字典中的位置,那么xi取值范围为{1,2,…|V|},|V|是字典中词的数目。这样一封邮件可以表示成![]() ,n可以变化,因为每封邮件的词的个数不同。然后我们对于每个xi随机从|V|个值中取一个,这样就形成了一封邮件。这相当于重复投掷|V|面的骰子,将观察值记录下来就形成了一封邮件。当然每个面的概率服从p(xi|y),而且每次试验条件独立。这样我们得到的邮件概率是
,n可以变化,因为每封邮件的词的个数不同。然后我们对于每个xi随机从|V|个值中取一个,这样就形成了一封邮件。这相当于重复投掷|V|面的骰子,将观察值记录下来就形成了一封邮件。当然每个面的概率服从p(xi|y),而且每次试验条件独立。这样我们得到的邮件概率是![]() 。居然跟上面的一样,那么不同点在哪呢?注意第一个的n是字典中的全部的词,下面这个n是邮件中的词个数。上面xi表示一个词是否出现,只有0和1两个值,两者概率和为1。下面的xi表示|V|中的一个值,|V|个p(xi|y)相加和为1。是多值二项分布模型。上面的x向量都是0/1值,下面的x的向量都是字典中的位置。
。居然跟上面的一样,那么不同点在哪呢?注意第一个的n是字典中的全部的词,下面这个n是邮件中的词个数。上面xi表示一个词是否出现,只有0和1两个值,两者概率和为1。下面的xi表示|V|中的一个值,|V|个p(xi|y)相加和为1。是多值二项分布模型。上面的x向量都是0/1值,下面的x的向量都是字典中的位置。
形式化表示为:
m个训练样本表示为:![]()
![]()
![]()
表示第i个样本中,共有ni个词,每个词在字典中的编号为![]() 。
。
那么我们仍然按照朴素贝叶斯的方法求得最大似然估计概率为
其中P(y)表示是垃圾邮件的概率。在p(y)的前提下向你发送特殊关键词的概率。n表示的是邮件词的个数,m是总样本数。
解得,
![]()
φk|y=1表示某人向你发送垃圾邮件时,他们会选择垃圾邮件出现的下一个词是k的概率。分子表示在样本中词k出现在垃圾邮件的次数。分母表示样本邮件中垃圾邮件所有词的总数。
φk|y=0表示某人向你发送非垃圾邮件时,他们会选择非垃圾邮件出现的下一个词是k的概率。
φy垃圾邮件占总样本的比例。
举个例子:(http://www.cnblogs.com/jerrylead/archive/2011/03/05/1971903.html)
X1 |
X2 |
X3 |
Y |
1 |
2 |
- |
1 |
2 |
1 |
- |
0 |
1 |
3 |
2 |
0 |
3 |
3 |
3 |
1 |
此时|V|=3,n1=n2=2,n3=n4=3,m为总试验次数。
假如邮件中只有a,b,c这三词,他们在词典的位置分别是1,2,3,前两封邮件都只有2个词,后两封有3个词。
Y=1是垃圾邮件。
那么,
![clip_image084[6] clip_image084[6]](http://img.e-com-net.com/image/info8/2b94eb082c874f2badc5ca06cfa6b14a.png) (在y=1的情况下出现x1-x3特征的次数所占出现词总数的比例)
(在y=1的情况下出现x1-x3特征的次数所占出现词总数的比例)
 (在y=0的情况下出现x1-x3特征的次数所占出现词总数的比例)
(在y=0的情况下出现x1-x3特征的次数所占出现词总数的比例)
假如新来一封邮件为b,c那么特征表示为{2,3}。
那么
那么该邮件是垃圾邮件概率是0.6。
注意这个公式与朴素贝叶斯的不同在于这里针对整体样本求的![]() ,而朴素贝叶斯里面针对每个特征求的
,而朴素贝叶斯里面针对每个特征求的![]() ,而且这里的特征值维度是参差不齐的。
,而且这里的特征值维度是参差不齐的。
这里如果假如拉普拉斯平滑,得到公式为:
表示每个k值至少发生过一次。注意这里分母加的是字典的总数,表示这个词在这个字典中出现过一次。
另外朴素贝叶斯虽然有时候不是最好的分类方法,但它简单有效,而且速度快。



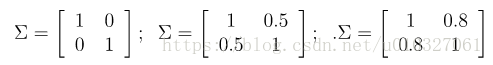





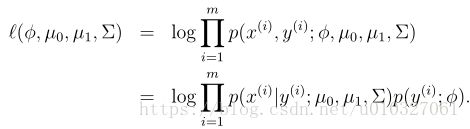
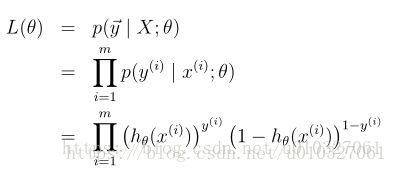






![clip_image081[6] 机器学习(八):CS229ML课程笔记(4)——生成学习,高斯判别分析,朴素贝叶斯_第17张图片](http://img.e-com-net.com/image/info8/6dcd8fec24fc42b8ac1e0f867065cc80.jpg)
![clip_image088[6] clip_image088[6]](http://img.e-com-net.com/image/info8/b360622c0af845c1b8c13d780eefd75e.png)
![clip_image090[6] clip_image090[6]](http://img.e-com-net.com/image/info8/830ee5f68265490da36b6db9af496147.png)
![clip_image097[6] 机器学习(八):CS229ML课程笔记(4)——生成学习,高斯判别分析,朴素贝叶斯_第18张图片](http://img.e-com-net.com/image/info8/d5752f7d236b451db0b558a19ef2282d.jpg)