形态学处理_木槿浅藏心_新浪博客

形态学处理

一. 实验目的

1.了解二值形态学的基本运算

2.掌握基本形态学图像的腐蚀、膨胀和开闭运算. 连接分量的标注的实现

3.了解形态操作的应用

二.实验基本原理

1.形态学

腐蚀和膨胀是数学形态学最基本的变换，数学形态学的应用几乎覆盖了图像处理的所有领域，给出利用数学形态学对二值图像处理的一些运算。膨胀就是把连接成分的边界扩大一层的处理。而收缩则是把连接成分的边界点去掉从而缩小一层的处理。

2.图像分割：

图像分割是图像处理的一个重要分支，研究为完成某一任务需要从图像中提取哪些有用的信息，以及如何利用这些信息解释图像。边缘检测技术对于处理数字图像非常重要，因为边缘是所要提取目标和背景的分界线，提取出边缘才能将目标和背景区分开来。在图像中，边界表明一个特征区域的终结和另一个特征区域的开始，边界所分开区域的内部特征或属性是一致的，而不同的区域内部的特征或属性是不同的，边缘检测正是利用物体和背景在某种图像特性上的差异来实现的，这些差异包括灰度，颜色或者纹理特征。边缘检测实际上就是检测图像特征发生变化的位置。图象边缘检测必须满足两个条件：一能有效地抑制噪声；二必须尽量精确确定边缘的位置

由于噪声和模糊的存在，检测到的边界可能会变宽或在某些点处发生间断，因此，边界检测包括两个基本内容：首先抽取出反映灰度变化的边缘点，然后剔除某些边界点或填补边界间断点，并将这些边缘连接成完整的线。边缘检测的方法大多数是基于方向导数掩模求卷积的方法。

导数算子具有突出灰度变化的作用，对图像运用导数算子，灰度变化较大的点处算得的值比较高，因此可将这些导数值作为相应点的边界强度，通过设置门限的方法，提取边界点集。

传统的边缘检测算法通过梯度算子来实现的，在求边缘的梯度时，需要对每个象素位置计算。在实际中常用小区域模板卷积来近似快速计算，简单有效，即梯度算子一般采用滤波算子的形式来完成，因此应用很广泛。模板是N*N的权值方阵，经典的梯度算子模板有：Sobel模板、Prewitt模板、Roberts模板、Laplacian模板等。拉普拉斯高斯（LoG）算法是一种二阶边缘检测方法。它通过寻找图像灰度值中二阶微分中的过零点（Zero Crossing）来检测边缘点。其原理为，灰度级变形成的边缘经过微风算子形成一个单峰函数，峰值位置对应边缘点；对单峰函数进行微分，则峰值处的微分值为0，峰值两侧符号相反，而原先的极值点对应二阶微分中的过零点，通过检测过零点即可将图像的边缘提取出来。

三．实验内容

1. 图像的腐蚀、膨胀和开闭运算

2. 连接分量的标注

3. 点/线的检测

4. 使用edge进行边缘检测（roberts/prewitt/sobel/LoG/Canny）

四、实验源代码及结果

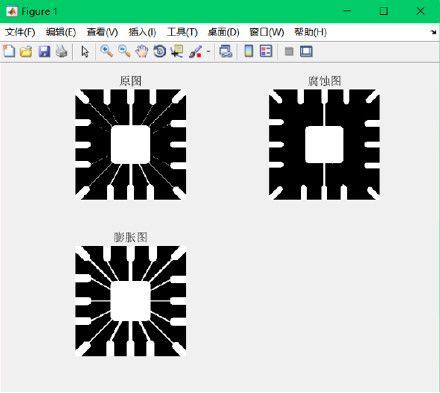
1.图像的腐蚀、膨胀:

clear;

close all;

SE=strel('rectangle',[5 5]);  %注意:结构元素必须具有适当的大小

BW1=imread('C:\Users\cs\Desktop\图片\结构.TIF')    

BW2=imerode(BW1,SE);    %腐蚀

BW3=imdilate(BW1,SE);    %膨胀

subplot(2,2,1),

imshow(BW1),title('原图');

subplot(2,2,2),

imshow(BW2),title('腐蚀图');

subplot(2,2,3),

imshow(BW3),title('膨胀图');

SE 不同，得到的效果也不同。

 

 

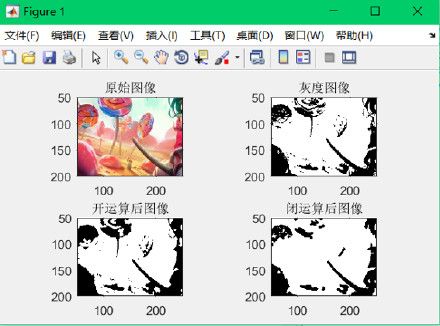
2.开闭运算：

I=imread('C:\Users\cs\Desktop\图片\波比.jpg');          %载入图像

subplot(2,2,1),imshow(I);

title('原始图像');

axis([50,250,50,200]);

axis on;                  %显示坐标系

I1=im2bw(I);

subplot(2,2,2),imshow(I1);

title('灰度图像');

axis([50,250,50,200]);

axis on;                  %显示坐标系 

%请改变结构元素大小，观察效果不同。如将半径改为5

se=strel('disk',2);     %采用半径为1的圆作为结构元素

I2=imopen(I1,se);         %开操作

I3=imclose(I1,se);        %闭操作

subplot(2,2,3),imshow(I2);

title('开运算后图像');

axis([50,250,50,200]);

axis on;                  %显示坐标系

subplot(2,2,4),imshow(I3);

title('闭运算后图像');

axis([50,250,50,200]);

axis on;                  %显示坐标系

结构参数设置不同，结果不一样。

 

 

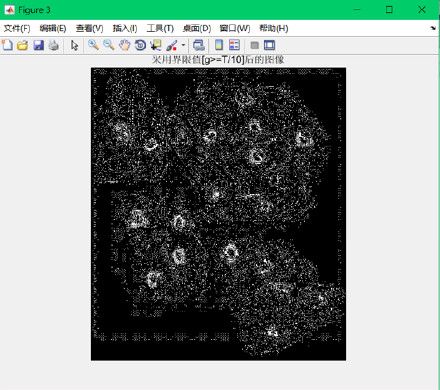
3.点检测：

clc

clear

f = imread(' C:\Users\cs\Desktop\图片\细胞.tif');

imshow(f)

title('原始图像')

w = [-1 -1 -1;

     -1  8 -1;

     -1 -1 -1];

g = abs(imfilter(double(f),w));

% **** 求矩阵最大值和对应坐标位置 ********

% [c1,i] = max(g);

% [c2,j] = max(c1);

% max_ans = g(i(j),j)      % 最大值

% max_location = [i(j),j]  % 最大值坐标位置

% **************************************

T = max(g(:));

g1 = g>=T/7;

% g2 = g>=T;

figure

imshow(g1)

title('采用界限值[g>=T/10]后的图像')

% figure

% imshow(g2)

% title('采用界限值[g>=T]后的图像')

 

4.线检测：

clc

clear

f = imread(' C:\Users\cs\Desktop\图片\X.TIF');

subplot(3,3,1),imshow(f)

title('原始连线掩模图像')

w = [2 -1 -1;

     -1 2 -1;

     -1 -1 2];

g = imfilter(double(f),w);

subplot(3,3,3),imshow(g,[])

title('-45度检测器处理后的图像')

gtop = g(1:120,1:120);

% gtop = pixeldup(gtop,4);

subplot(3,3,4),imshow(gtop,[])% imshow(gtop,'InitialMagnification','fit')

title('左上角的放大图')

%

gbot = g(end-119:end,end-119:end);

% gbot = pixeldup(gbot,4);

subplot(3,3,6),imshow(gbot,[])

title('右下角的放大图')

 

 5.边缘检测：

分别用Roberts,Sobel和拉普拉斯高斯算子对图像进行边缘检测。比较三种算子处理的不同之处；

I=imread(‘C:\Users\cs\Desktop\图片\.tif');

imshow(I)

BW1=edge(I,'roberts');

figure ,imshow(BW1),title('用Roberts算子')

BW2=edge(I,'sobel');

figure,imshow(BW2),title('用Sobel算子 ')

BW3=edge(I,'log');

figure,imshow(BW3),title('用拉普拉斯高斯算子')

得到：

比较提取边缘的效果可以看出，sober算子是一种微分算子，对边缘的定位较精确，但是会漏去一些边缘细节。而Laplacian-Gaussian算子是一种二阶边缘检测方法，它通过寻找图像灰度值中二阶过零点来检测边缘并将边缘提取出来，边缘的细节比较丰富。通过比较可以看出Laplacian-Gaussian算子比sober算子边缘更完整，效果更好。

 

五．实验总结（心得体会）

通过这次实验我明白了利用形态学的知识对图片进行处理，通过物体和结构元素的相互作用，得到更本质的形态，知道了形态运算是并行运算。