【书籍阅读 Ch4】Reinforcement Learning An Introduction, 2nd Edition
Chapter 4: Dynamic Programming
- 回顾与进入
- 4.1 Policy Evaluation
-
- RPage:74 式子4.5下
- 伪代码对应
- Figure 4.1
- 4.2 Policy Improvement
-
- 伪代码对应
- 4.3 Policy Iteration
-
- Example 4.2 car_rental
- 4.4 Value Iteration
-
- 伪代码对应
- All Exercise Part
前言:第1、2章点此进入;第3章点此进入
注:每一个目录对应的是在pdf的页数(如果LPage就是书左上角的页码 - 因为我发现后面我要在两页之间加空白页 做练习lol 例如:LPage28 就是左上角书页28页,RPage29就是右上角书页29页);【】这个括号之间有时候是我留的疑问,与一些关于方向上连接的想法 主要集中于无人驾驶的控制层,带问号结束的就是…我的疑问
更新时间:2021/01/14
推荐观看:
1.英文 - PDF链接
2 中文 - 官方京东书籍购买链接
代码参考:
1.github 关于整本书的图python代码
2.github 关于整本书的练习solution参考
回顾与进入
在上一章节中我们提出了怎样构建强化学习的MDP及数学公式的推导,那么怎样计算呢?从传统的方法首先是动态规划(Dynamic Programming) 局限性:
- their assumption of a prefect model (假设模型完整且拥有所有信息)
- their great computational expense (随着状态环境的复杂,需要很多算力)
The key idea of DP, and of reinforcement learning generally, is the use of value functions to organize and structure the search for good policies.
而这一节也就是怎样使用DP去计算第三章所提出的value function,其实DP就是一个迭代的方式,可以说是for-for 判断误差小于一定值
满足Bellman equation的 v ∗ v_* v∗ 和 q ∗ q_* q∗
v ∗ ( s ) = max a E [ R t + 1 + γ v ∗ ( S t + 1 ) ∣ S t = s , A t = a ] = max a ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v ∗ ( s ′ ) ] \begin{aligned} v_{*}(s) &=\max _{a} \mathbb{E}\left[R_{t+1}+\gamma v_{*}\left(S_{t+1}\right) \mid S_{t}=s, A_{t}=a\right] \\ &=\max _{a} \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{*}\left(s^{\prime}\right)\right] \end{aligned} v∗(s)=amaxE[Rt+1+γv∗(St+1)∣St=s,At=a]=amaxs′,r∑p(s′,r∣s,a)[r+γv∗(s′)]
4.1 Policy Evaluation
RPage:74 式子4.5下
为什么Clearly, v k = v π v_k=v_\pi vk=vπ is a fixed point for this update rule?式子4.5相对于式子4.4的迭代不仅仅只是state了value function的下标也从 π \pi π变到了k -> k+1。式子4.5等号前的下标k+1意味着? 疑惑点
自答:k表示不同时间对于state s的更新
伪代码对应
def compute_state_value(in_place=True, discount=1.0):
new_state_values = np.zeros((WORLD_SIZE, WORLD_SIZE))
iteration = 0
# Loop one
while True:
if in_place:
state_values = new_state_values #可以理解为地址的指向,所以会随着new变
else:
state_values = new_state_values.copy() #这种.copy的情况下 states_values是不会随着new的变化而变化的
old_state_values = state_values.copy()
# Loop two: for each s in States
for i in range(WORLD_SIZE):
for j in range(WORLD_SIZE):
value = 0
# every action in ACTIONS
for action in ACTIONS:
(next_i, next_j), reward = step([i, j], action)
value += ACTION_PROB * (reward + discount * state_values[next_i, next_j])
# V(s) update
new_state_values[i, j] = value
# /delta <- max(/delta,abs(v-V(s)))
max_delta_value = abs(old_state_values - new_state_values).max()
# until /delta < /theta
if max_delta_value < 1e-4:
break
iteration += 1
return new_state_values, iteration
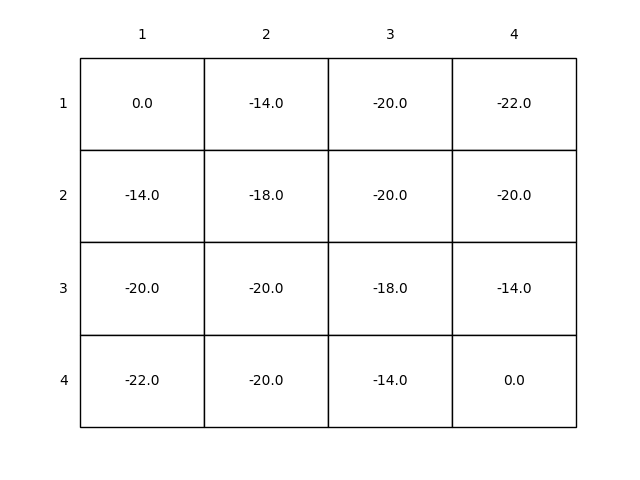
Figure 4.1
#######################################################################
# Copyright (C) #
# 2016-2018 Shangtong Zhang([email protected]) #
# 2016 Kenta Shimada([email protected]) #
# Permission given to modify the code as long as you keep this #
# declaration at the top #
#######################################################################
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.table import Table
# matplotlib.use('Agg')
WORLD_SIZE = 4
# left, up, right, down
ACTIONS = [np.array([0, -1]),
np.array([-1, 0]),
np.array([0, 1]),
np.array([1, 0])]
ACTION_PROB = 0.25
def is_terminal(state):
x, y = state
return (x == 0 and y == 0) or (x == WORLD_SIZE - 1 and y == WORLD_SIZE - 1)
def step(state, action):
if is_terminal(state):
return state, 0
next_state = (np.array(state) + action).tolist()
x, y = next_state
if x < 0 or x >= WORLD_SIZE or y < 0 or y >= WORLD_SIZE:
next_state = state
reward = -1
return next_state, reward
def draw_image(image):
fig, ax = plt.subplots()
ax.set_axis_off()
tb = Table(ax, bbox=[0, 0, 1, 1])
nrows, ncols = image.shape
width, height = 1.0 / ncols, 1.0 / nrows
# Add cells
for (i, j), val in np.ndenumerate(image):
tb.add_cell(i, j, width, height, text=val,
loc='center', facecolor='white')
# Row and column labels...
for i in range(len(image)):
tb.add_cell(i, -1, width, height, text=i+1, loc='right',
edgecolor='none', facecolor='none')
tb.add_cell(-1, i, width, height/2, text=i+1, loc='center',
edgecolor='none', facecolor='none')
ax.add_table(tb)
def compute_state_value(in_place=True, discount=1.0):
new_state_values = np.zeros((WORLD_SIZE, WORLD_SIZE))
iteration = 0
while True:
if in_place:
state_values = new_state_values
else:
state_values = new_state_values.copy()
old_state_values = state_values.copy()
for i in range(WORLD_SIZE):
for j in range(WORLD_SIZE):
value = 0
for action in ACTIONS:
(next_i, next_j), reward = step([i, j], action)
value += ACTION_PROB * (reward + discount * state_values[next_i, next_j])
new_state_values[i, j] = value
max_delta_value = abs(old_state_values - new_state_values).max()
if max_delta_value < 1e-4:
break
iteration += 1
return new_state_values, iteration
def figure_4_1():
# While the author suggests using in-place iterative policy evaluation,
# Figure 4.1 actually uses out-of-place version.
_, asycn_iteration = compute_state_value(in_place=True)
values, sync_iteration = compute_state_value(in_place=False)
draw_image(np.round(values, decimals=2))
print('In-place: {} iterations'.format(asycn_iteration))
print('Synchronous: {} iterations'.format(sync_iteration))
plt.savefig('../images/figure_4_1.png')
plt.close()
if __name__ == '__main__':
figure_4_1()
4.2 Policy Improvement
对应下面4.3伪代码的第三部分 policy improvement
伪代码对应
# policy improvement
policy_stable = True
for i in range(MAX_CARS + 1):
for j in range(MAX_CARS + 1):
old_action = policy[i, j]
action_returns = []
for action in actions:
if (0 <= action <= i) or (-j <= action <= 0):
action_returns.append(expected_return([i, j], action, value, constant_returned_cars))
else:
action_returns.append(-np.inf)
new_action = actions[np.argmax(action_returns)]
policy[i, j] = new_action
if policy_stable and old_action != new_action:
policy_stable = False
print('policy stable {}'.format(policy_stable))
4.3 Policy Iteration
Example 4.2 car_rental
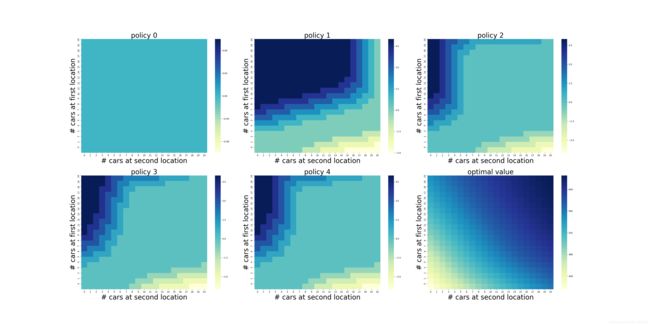
对于杰克租车问题,一开始一直没理解这个图是个啥意思,后面知道了 所以也算解释一下:
横纵坐标轴是在地点二、一的车辆数,比如我们看policy 1下,放大看哈,当地点一有四辆车(纵坐标),地点二没有车时(横坐标),整个策略是将地点一的一辆车移到地点二(热力图的对应点);问:那么现在可以看看policy 4时,当地点一有20辆车、地点二没有车时,我们的策略是?
答:+5:也就是从一移五辆车到二
#######################################################################
# Copyright (C) #
# 2016 Shangtong Zhang([email protected]) #
# 2016 Kenta Shimada([email protected]) #
# 2017 Aja Rangaswamy ([email protected]) #
# Permission given to modify the code as long as you keep this #
# declaration at the top #
#######################################################################
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from scipy.stats import poisson
matplotlib.use('Agg')
# maximum # of cars in each location
MAX_CARS = 20
# maximum # of cars to move during night
MAX_MOVE_OF_CARS = 5
# expectation for rental requests in first location
RENTAL_REQUEST_FIRST_LOC = 3
# expectation for rental requests in second location
RENTAL_REQUEST_SECOND_LOC = 4
# expectation for # of cars returned in first location
RETURNS_FIRST_LOC = 3
# expectation for # of cars returned in second location
RETURNS_SECOND_LOC = 2
DISCOUNT = 0.9
# credit earned by a car
RENTAL_CREDIT = 10
# cost of moving a car
MOVE_CAR_COST = 2
# all possible actions
actions = np.arange(-MAX_MOVE_OF_CARS, MAX_MOVE_OF_CARS + 1)
# An up bound for poisson distribution
# If n is greater than this value, then the probability of getting n is truncated to 0
POISSON_UPPER_BOUND = 11
# Probability for poisson distribution
# @lam: lambda should be less than 10 for this function
poisson_cache = dict()
def poisson_probability(n, lam):
global poisson_cache
key = n * 10 + lam
if key not in poisson_cache:
poisson_cache[key] = poisson.pmf(n, lam)
return poisson_cache[key]
def expected_return(state, action, state_value, constant_returned_cars):
"""
@state: [# of cars in first location, # of cars in second location]
@action: positive if moving cars from first location to second location,
negative if moving cars from second location to first location
@stateValue: state value matrix
@constant_returned_cars: if set True, model is simplified such that
the # of cars returned in daytime becomes constant
rather than a random value from poisson distribution, which will reduce calculation time
and leave the optimal policy/value state matrix almost the same
"""
# initailize total return
returns = 0.0
# cost for moving cars
returns -= MOVE_CAR_COST * abs(action)
# moving cars
NUM_OF_CARS_FIRST_LOC = min(state[0] - action, MAX_CARS)
NUM_OF_CARS_SECOND_LOC = min(state[1] + action, MAX_CARS)
# go through all possible rental requests
for rental_request_first_loc in range(POISSON_UPPER_BOUND):
for rental_request_second_loc in range(POISSON_UPPER_BOUND):
# probability for current combination of rental requests
prob = poisson_probability(rental_request_first_loc, RENTAL_REQUEST_FIRST_LOC) * \
poisson_probability(rental_request_second_loc, RENTAL_REQUEST_SECOND_LOC)
num_of_cars_first_loc = NUM_OF_CARS_FIRST_LOC
num_of_cars_second_loc = NUM_OF_CARS_SECOND_LOC
# valid rental requests should be less than actual # of cars
valid_rental_first_loc = min(num_of_cars_first_loc, rental_request_first_loc)
valid_rental_second_loc = min(num_of_cars_second_loc, rental_request_second_loc)
# get credits for renting
reward = (valid_rental_first_loc + valid_rental_second_loc) * RENTAL_CREDIT
num_of_cars_first_loc -= valid_rental_first_loc
num_of_cars_second_loc -= valid_rental_second_loc
if constant_returned_cars:
# get returned cars, those cars can be used for renting tomorrow
returned_cars_first_loc = RETURNS_FIRST_LOC
returned_cars_second_loc = RETURNS_SECOND_LOC
num_of_cars_first_loc = min(num_of_cars_first_loc + returned_cars_first_loc, MAX_CARS)
num_of_cars_second_loc = min(num_of_cars_second_loc + returned_cars_second_loc, MAX_CARS)
returns += prob * (reward + DISCOUNT * state_value[num_of_cars_first_loc, num_of_cars_second_loc])
else:
for returned_cars_first_loc in range(POISSON_UPPER_BOUND):
for returned_cars_second_loc in range(POISSON_UPPER_BOUND):
prob_return = poisson_probability(
returned_cars_first_loc, RETURNS_FIRST_LOC) * poisson_probability(returned_cars_second_loc, RETURNS_SECOND_LOC)
num_of_cars_first_loc_ = min(num_of_cars_first_loc + returned_cars_first_loc, MAX_CARS)
num_of_cars_second_loc_ = min(num_of_cars_second_loc + returned_cars_second_loc, MAX_CARS)
prob_ = prob_return * prob
returns += prob_ * (reward + DISCOUNT *
state_value[num_of_cars_first_loc_, num_of_cars_second_loc_])
return returns
def figure_4_2(constant_returned_cars=True):
value = np.zeros((MAX_CARS + 1, MAX_CARS + 1))
policy = np.zeros(value.shape, dtype=np.int)
iterations = 0
_, axes = plt.subplots(2, 3, figsize=(40, 20))
plt.subplots_adjust(wspace=0.1, hspace=0.2)
axes = axes.flatten()
while True:
fig = sns.heatmap(np.flipud(policy), cmap="YlGnBu", ax=axes[iterations])
fig.set_ylabel('# cars at first location', fontsize=30)
fig.set_yticks(list(reversed(range(MAX_CARS + 1))))
fig.set_xlabel('# cars at second location', fontsize=30)
fig.set_title('policy {}'.format(iterations), fontsize=30)
# policy evaluation (in-place)
while True:
old_value = value.copy()
for i in range(MAX_CARS + 1):
for j in range(MAX_CARS + 1):
new_state_value = expected_return([i, j], policy[i, j], value, constant_returned_cars)
value[i, j] = new_state_value
max_value_change = abs(old_value - value).max()
print('max value change {}'.format(max_value_change))
if max_value_change < 1e-4:
break
# policy improvement
policy_stable = True
for i in range(MAX_CARS + 1):
for j in range(MAX_CARS + 1):
old_action = policy[i, j]
action_returns = []
for action in actions:
if (0 <= action <= i) or (-j <= action <= 0):
action_returns.append(expected_return([i, j], action, value, constant_returned_cars))
else:
action_returns.append(-np.inf)
new_action = actions[np.argmax(action_returns)]
policy[i, j] = new_action
if policy_stable and old_action != new_action:
policy_stable = False
print('policy stable {}'.format(policy_stable))
if policy_stable:
fig = sns.heatmap(np.flipud(value), cmap="YlGnBu", ax=axes[-1])
fig.set_ylabel('# cars at first location', fontsize=30)
fig.set_yticks(list(reversed(range(MAX_CARS + 1))))
fig.set_xlabel('# cars at second location', fontsize=30)
fig.set_title('optimal value', fontsize=30)
break
iterations += 1
plt.savefig('../images/figure_4_2.png')
plt.close()
if __name__ == '__main__':
figure_4_2()
4.4 Value Iteration
Policy Iteration 策略迭代的缺点从伪代码中就可以看出 两次Loop 第一次Loop就已经是所有状态里找了,第二次还需要从所有状态里判断,而从图4.1我们可以看出 其实提前打断Policy evaluation 也不会对最终的最优policy有问题
一次遍历后即可停止策略评估的Loop 对每个状态都更新,也就是value iteration 价值迭代
v k + 1 ( s ) = max a E [ R t + 1 + γ v k ( S t + 1 ) ∣ S t = s , A t = a ] = max a ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v k ( s ′ ) ] \begin{aligned} v_{k+1}(s) &=\max _{a} \mathbb{E}\left[R_{t+1}+\gamma v_{k}\left(S_{t+1}\right) \mid S_{t}=s, A_{t}=a\right] \\ &=\max _{a} \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{k}\left(s^{\prime}\right)\right] \end{aligned} vk+1(s)=amaxE[Rt+1+γvk(St+1)∣St=s,At=a]=amaxs′,r∑p(s′,r∣s,a)[r+γvk(s′)]
伪代码对应
也就是在选择动作时 顺便直接选择最大value的max action

# value iteration
while True:
old_state_value = state_value.copy() #把所有的old states value都复制了
sweeps_history.append(old_state_value)
for state in STATES[1:GOAL]:
# get possilbe actions for current state
actions = np.arange(min(state, GOAL - state) + 1)
action_returns = []
for action in actions:
action_returns.append(
HEAD_PROB * state_value[state + action] + (1 - HEAD_PROB) * state_value[state - action])
new_value = np.max(action_returns) # 选取最大的a
state_value[state] = new_value # 赋值V(s)
delta = abs(state_value - old_state_value).max()
if delta < 1e-9:
sweeps_history.append(state_value)
break

