Reinforcement Learning: An Introduction Second Edition - Chapter 9

Part II Approximate Solution Methods

拥有任意大的状态空间的问题。目标：使用有限的计算资源找到一个比较好的近似解。

除了内存，还有时间和数据。从以往经历的与当前状态在某种程度上相似的状态中去归纳 $\to$ 泛化能力。

有很多泛化方法可以直接在强化学习中使用。函数逼近：从一个预期的函数(如价值函数)中获取实例，并试图对它们进行泛化来逼近整个函数。函数逼近是有监督学习的一个实例，是很多领域的基础方法。理论上，这些领域研究的任何方法都可以在强化学习算法中用作函数逼近器，尽管在实践中有些方法比其他方法更容易发挥这种作用。

带有函数逼近的强化学习会出现在传统的监督学习中通常不会出现的新问题。

9 On-policy Prediction with Approximation

Estimating the state-value function from on-policy data.

近似的价值函数是一个具有权值向量的参数化函数。例子：控制论，ANNs，决策树。通常权值数量远远小于状态数量（注：否则会过拟合）。改变一个权值将改变很多状态的估计值。

函数逼近有助于解决部分可观测问题。

9.1 Value-function Approximation

预测方法：对一个待估计的价值函数的更新。

更新某个状态时，其他状态的估计价值同样发生变化。有监督学习：拟合输入输出样例。当输出为数字是，这个过程被称为函数逼近。我们把每次的更新作为函数逼近的价值函数预测的训练样本，然后把产生的近似函数作为估计价值函数。

我们可以使用几乎所有的函数逼近方法来进行价值函数预测，但其实并不是所有的方法都适用于强化学习。对方法的要求：从逐步得到的数据中学习；能够处理非平稳目标函数。

9.2 The Prediction Objective ($\overline{VE}$)

对预测质量进行连续的衡量。根据假设，状态远远多于权值，所以一个状态的估计越准确，无一例外地意味着让其他状态的估计变得不那么准确。给出对每个状态的重视程度。一个自然的目标函数：均方价值误差，$\overline{VE}$。

通常权重 $\mu (s)$ 是在状态s上消耗的计算时间的比例。在同轨策略训练中，$\mu (s)$ 被称为同轨策略分布。在持续性任务中它是稳定分布。在分幕式任务中，$\mu (s)$ 与幕的初始状态的选取有关（注：在分幕式任务中，$\mu (s)$ 也是一个稳定分布，不过因为每幕都有起始状态，所以和持续性任务不同。以上讨论的前提是，状态转移函数不变(在目前的范畴中，问题的状态转移函数好像一直是不变的。非平稳RL问题仅仅指状态的收益随时间变化?)）。如果存在折扣，则应视其为一种终止形式（非平稳问题需要折扣。此时 $\mu (s)$ 是一个动态分布）。

在对近似求解进行正式分析中，持续性任务和分幕式任务应该分开讨论。

目前还不能确定 $\overline{VE}$ 是否是强化学习正确的性能目标。

全局最优的权值向量 ${\mathbf{w}}^{\ast }$ $\leftarrow$ simple function approximators: linear function approximators…
局部最优的权值向量 ${\mathbf{w}}^{\ast }$ $\leftarrow$ complex function approximators (nonlinear function approximators): artificial neural networks, decision trees…

许多强化学习案例仍然无法保证收敛到一个最优值，甚至最优值附近的某个边界距离内。

预测的框架：用强化学习方法的更新来生成函数逼近方法的训练数据。试图最小化的性能度量：$\overline{VE}$ 。

9.3 Stochastic-gradient and Semi-gradient Methods

注：梯度上升算法用来求函数的最大值， 梯度下降算法用来求函数的最小值。

一类用于价值函数预测的基于随机梯度下降(SGD)的函数逼近的学习方法，其特别适用于在线强化学习。

$\mathbf{w}$ 是由固定实数组成的列向量。即使我们获得了所有 $S_t$ 的价值函数，由于计算资源有限，我们也只能给出受限的精确度。一般不存在 $\mathbf{w}$ 可以使得价值函数精确计算所有状态，甚至所有样本。

假设样本中的分布 $\mu$ 与公式中的相同。SGD求所有偏导，所得的导数向量是函数关于 $\mathbf{w}$ 的梯度。注：可以使用一个一元一次函数的梯度下降的例子来理解。

小步长更新：我们不期望对每个状态都将误差消除为零。SGD方法的收敛性建立在 $\alpha$ 随时间减小的假设上（局部最优解）。

通用SGD方法：用一个近似值取代 $v(S_t)$。

梯度蒙特卡洛算法：蒙特卡洛状态价值函数预测的梯度下降版本。

使用自举估计值无法获得收敛性保证。自举目标 $U_t$ 是有偏的，SGD的目标必须与 ${\mathbf{w}}_{\mathbf{t}}$ 无关。自举法只考虑了改变权值向量 ${\mathbf{w}}_{\mathbf{t}}$ 对估计的影响，而忽略了 ${\mathbf{w}}_{\mathbf{t}}$ 对目标的影响。由于只含有一部分梯度，我们称之为半梯度方法。

由于一些优点，半梯度(自举法)方法通常是首选方案。它们的学习速度通常比较快；它们支持持续地在线地学习。一个典型的半梯度方法：半梯度TD(0)。

State aggregation：权值的一个维度分量，对应一组状态。

例 9.1 使用状态聚合的随机游走：the gradient Monte-Carlo algorithm with state aggregation (function approximation by state aggregation using the gradient Monte Carlo algorithm). 状态聚合的典型特征：阶梯效果。

9.4 Linear Methods

函数逼近最重要的特殊情况之一：近似函数是权值向量的线性函数。

状态 s 对应的一个函数值称作 s 的一个特征。对于线性方法，特征被称作基函数(basis functions)，它们构成了近似函数集合的一个线性基。构建 d 维特征向量以表示状态，与选择一组 d 个基函数是一样的。定义特征的多种方式，将在接下来的章节介绍一些方式。

在线性逼近中，近似价值函数关于 $\mathbf{w}$ 的梯度为向量 $\mathbf{x}(s)$。因为线性SGD非常简单，

在线性情况下，函数只存在一个最优值，因此很多方法可以自动地保证收敛到全局最优值。

半梯度TD(0)算法，其收敛到的权值向量不是全局最优，而是靠近局部最优的一点。

线性TD(0)收敛性证明：关键矩阵和矩阵 $\mathbf{A}$ 的正定性。

TD方法学习速度更快，MC方法长期性能更好。

同轨策略的自举法的误差边界。linear semi-gradient DP 也会收敛到TD不动点。One-step semi-gradient action-value methods, such as semi-gradient Sarsa(0)，也会收敛到类似的不动点和类似的误差边界。分幕式的情况有一个略微不同但相似的边界。

以上收敛的关键：状态是按照同轨策略分布来更新的。否则使用函数逼近的自举法可能发散到无穷大。

例 9.2 1000 状态随机游走任务上的自举法：状态聚合是线性函数逼近的一个特例。TD方法以及广义MC方法在学习速率方面仍然有很大的潜在优势。

练习 9.1：表格型方法是线性逼近法的状态减少到一定数量的一种特例；可以将表格型方法理解为每组只有一个状态的状态聚合；可以通过将线性方法的等式转化为表格型方法的等式来证明。此时特征向量是一个布尔型变量，状态为对应状态时其值为1，否则为0。

9.5 Feature Construction for Linear Methods

线性方法在数据和计算方面非常高效，但这很大程度上取决于状态如何用特征来表示。选择适合任务的特征是将先验知识加入强化学习系统的一个重要方式。直观地说，这些特征应该提取状态空间中最通用的信息。注：特征和状态的关系？状态对应的一个特征向量函数值，称作状态的一个特征。我们需要从状态中直接选择，或进行构造特征。状态的表达方式不同，特征的类型不同。不同类型的特征有不同的构造方式，本节会讨论各种类特征的表示/构造方法。

线性形式的一个局限性在于它无法表示特征之间的相互作用。它需要将相互作用的基本状态维度结合起来加入特征中。

9.5.1 Polynomial Basis

通过数字表达状态的问题。

n阶多项式基。

n阶多项式基的特征数量随着状态空间维度呈指数增长，通常选择一个子集进行函数逼近。可以根据待近似函数的性质的先验知识进行特征选择，也可以使用一些多项式回归中常用的特征自动选择方法，但需要针对强化学习进行一些调整。

练习 9.2：因为对于每个状态，都有 $n+1$ 阶可以选择。

练习 9.3：n=2，$c_{i,j}\in$ {0, 1, 2}。

9.5.2 Fourier Basis

傅里叶级数：将周期函数表示为正弦和余弦基函数(特征)的加权和。傅里叶变换。注：为什么多项式基的性能不如傅里叶基？因为多项式基想要十分逼近一个函数更加复杂？

首先考虑一维情况（基函数的输入是一维，即状态空间是一维；状态维度和特征数量不相关）。周期为 $\tau$ 的一维函数的傅里叶级数通常是正弦函数和余弦函数的线性组合，这些函数的周期可以被 $\tau$ 整除。对于有界区间内定义的非周期函数，也可以使用傅里叶基函数，并将周期设置为区间的长度。

将 $\tau$ 设置为感兴趣区间长度的两倍。

一维 n 阶傅里叶余弦基由 n+1 个特征构成。

多维情况下的傅里叶余弦级数近似。傅里叶基的这些特征可以被平移和缩放，以适应特定应用的有界状态空间。例子：根据图中标记的向量 $\mathbf{c}$ 可知，这是五阶甚至更高阶的傅里叶基。

在一些学习算法中使用傅里叶余弦特征时，不同的特征最好使用不同的步长参数。先设置一个基础的步长参数，对于每一个特征，步长参数根据基础参数和向量 $\mathbf{c}$ 进行调整。

傅里叶特征在不连续性方面存在问题。

状态维度小：使用所有 n 阶傅里叶特征，此时特征的选择或多或少是自动的(被动)。状态维度大：使用一个特征的子集，通过先验知识或自动选择方法(主动)选取被使用的特征。通过限制向量 $\mathbf{c}$ 的值，使近似值去除那些被认为是噪声的高频成分。由于傅里叶特征几乎是非零的，所以可以说它们表征了状态的全局特性，然而这使得表征局部特征变得困难。

一般不建议使用多项式基进行在线学习。

9.5.3 Coarse Coding

假设一个状态集在一个连续二维空间上。二值特征。基于二值特征s，粗略地对状态的位置进行编码。使用特征的这种重叠(不一定非是圆圈或二进制)来表示一个状态，被称为粗编码。

圆的大小和密度对SGD函数逼近的影响(圆的密度，即特征的密度)。每个圆对应权值向量的一个分量。泛化：训练一个状态使得所有相关的圆都受到影响，因此并集内所有状态的估计价值都会受到影响。

注：粗编码的基函数是什么？一个状态到布尔值的映射？即 $x_i(s)=1$，如果状态 s 在特征 $x_i$ 的范围内 ？这如何体现泛化，即对同特征状态的影响？答：同特征的状态价值是完全相等的。
注：特征过多，可能会造成过拟合。

感受野的形状对于泛化有着巨大的影响，但对于渐进解的质量影响很小。

9.5.4 Tile Coding

一种用于多维连续空间的粗编码（注：仍然是二维？）。对于时序数字计算机来说，它也许是最为实用的特征表达方式。仅使用一次 覆盖，我们得到的并不是粗编码而是状态聚合的一个特例。

相互重叠的感受野。特征向量x(s)在每个覆盖的每个瓦片上都有一个分量。

使用非对称偏移，使被训练状态的泛化更均匀，更接近球形。

覆盖的偏移量与瓦片宽度成比例。

不同的位移向量对瓦片编码的泛化能力的影响。

覆盖的个数和瓦片的形状。

不同的覆盖最好使用不同形状的瓦片。仅凭条形瓦片不可能学习到水平和垂直坐标的任意组合具有的独特的价值。覆盖的选择决定了泛化能力。

哈希如何保证每个状态激活的特征数相同？如果每个覆盖随机选取的瓦片的总面积是相等的，根据大数定律，能保证状态的特征数大致相等。

练习 9.4：应该采用沿着重要维度切割的条形瓦片的覆盖，以及正方形瓦片的覆盖的组合。这样就能兼顾重要维度上的泛化以及对特定坐标组合的价值的学习。

9.5.5 Radial Basis Functions

径向基函数(RBF)是粗编码在连续值特征中的自然推广。

在高维情况下，瓦片的边界更为重要，而响应函数的分级十分困难。

RBF网络和非线性RBF网络。

9.6 Selecting Step-Size Parameters Manually

练习 9.5：根据题意和公式(9.19)，我们只要得到特征向量的平方和的期望，就可以得到步长参数。当七维状态空间中有一维发生变化时，会有（$1\times 8+6\times 2$）个特征出席，因此我们可以得到，步长参数$\alpha =(10\ast 20{)}^{-1}$ 。

9.7 Nonlinear Function Approximation: Artificial Neural Networks

ANNs被广泛应用于非线性函数逼近。一个ANN是由相互连接的单元组成的网络。

前馈ANNs：网络中没有一个单元的输出可以影响它自身的输入。四个概念：输入、输出、隐层、权值。
循环ANNs：在网络的连接中至少有一个环。

ANNs的单元一般是半线性的，它首先计算输入信号的加权和，然后对结果应用非线性函数，激活函数，最后得到单元的输出。网络的输入层的激活依靠输入值。

对于回归问题，我们一般使用恒等函数作为输出单元的激活函数。网络的连接权值就是函数的参数。没有隐层；一个隐层。激活函数的非线性很重要：如果一个多层前馈ANN中的所有单元都是线性激活函数，那么整个网络就相当于一个没有隐藏层的网络（因为线性函数的线性函数仍然是线性的）。

虽然单隐藏层的ANN可以逼近任何函数，但是多隐藏层的ANN更容易逼近复杂函数，因为多层ANN可以产生抽象。深度架构可以将许多层低级抽象层次化组合为高级抽象，来帮助逼近复杂函数。深度ANN的每一个计算单元提供一个特征。

训练ANN的隐藏层是一种自动发现适合给定问题的特征的方法。它可以自动获得层次化的表征而不需要人工设计的特征。ANN一般用SGD方法训练。ANN需要一个最大化或最小化的目标函数来衡量性能。在强化学习中，ANN可以最小化TD误差，或者最大化期望收益，或者使用策略梯度算法。

求ANN梯度的方法：反向传播算法，交替进行前向和反向传播过程。

反向传播法可以很好地应用于含有1到2个隐藏层的网络中。训练深层次网络往往会得到更差的性能。问题：过拟合；偏导在反向计算中快速变大变小。解决这些问题的方法s，帮助深度ANN在最近取得了许多令人印象深刻的成果。

过拟合：任何函数逼近方法在有限数据上训练多自由度函数的常见问题。在线强化学习中过拟合并不突出，但有效泛化仍是一个重要问题；过拟合是ANN的普遍问题，在深度ANN中尤为突出。防止过拟合的方法：cross validation，regularization，引入权重之间的依赖关系以减小自由度(如参数共享)等。

一个防止深度ANN过拟合的特别有效的方法：the dropout method。这种方法可以显著提高泛化能力。它促使每个独立的隐层单元学到与其他特征的随机组合配合得很好的特征。

Hinton等人(2006)在如何训练深层的ANN方面取得了重要的进展：先使用无监督学习从网络最深层开始对每一层依次进行训练，将训练后的权值作为有监督学习的初始权值，然后根据目标函数利用反向传播算法继续调整权值[1]。对这种方法的一种解释是它可以把网络的权值预训练到一个比较适合梯度方法调整的区域。

Batch normalization: 提高学习率，不依赖初始值，抑制过拟合。思路：将输入的值归一化。在较深层的输出(mini-batches)在输入给下一层之前，进行归一化。

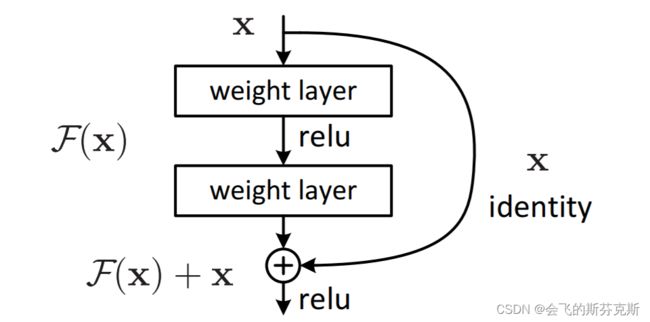
深度残差学习：帮助训练深度ANN，解决层数增加导致的网络性能退化。有时，学习一个函数和恒等函数的区别比学习这个函数本身更容易。我们把这个差值，或称残差函数，加到输入中，就产生了所需的函数（注：此时可以把输出理解为，残值函数+恒等函数）。下图为残差学习单元[2]。

深度卷积网络（deep convolutional networks，卷积神经网络CNN），一类典型的深度ANN。高维空间数据，如图像。由于它的特殊结构，深度卷积网络可以直接利用反向传播算法来优化，而不需借助前面介绍的训练深度层的各种方法。

相比于全连接的神经网络，深度卷积网络考虑了数据的形状[3]。卷积层的输入输出数据被称为“特征图”。同一特征图中的不同单元共享相同的权值。这意味着，无论特征图在输入阵列中位于何处，它都能检测到相同的特征。注：每一层有多个权值，产生多张特征图。

深度卷积网络的下采样层的作用是降低特征图的空间分辨率。下采样层中特征图的每一单元是前一个卷积层的特征图中感受野内的单元的平均。下采样层使得网络对特征所处的空间位置不敏感，即可以使网络的输出有空间不变性。

9.8 Least-Squares TD

一种线性函数逼近方法。之前的方法每一时刻需要正比于参数的计算量，而 Least-Squares TD 使用更多的计算得到了更好的效果。

不采取迭代法，而是根据数据，直接计算TD不动点。注：数据效率，即数据的利用率。

9.9 Memory-based Function Approximation

与参数化方法很不同，基于记忆的方法仅仅保存训练样本而不更新参数。每当查询估计值时从内存中找出样本的集合来计算查询状态的估计值。也称 lazy learning。

非参数化方法：不局限于一个固定的参数化的函数类，而是由训练样本以及将它们结合起来为查询状态输出估计值的方法共同决定。

不同基于记忆的方法：训练样本的选择和使用。local-learning：使用查询状态的相邻的状态来估计其价值函数的近似值。样本与查询状态的相关性取决于距离，距离有许多方法可以定义。

最近邻法。加权平均法。局部加权回归。

非参数化方法：不需要将近似值限制在预先指定的函数形式。基于记忆的局部近似法。轨迹采样。没有必要进行全局近似估计，因为状态空间中的许多区域永远不会被访问到。

避免全局估计是解决维度灾难的一种方法。基于记忆的方法的关键问题：能否足够快地回复对智能体有用的查询。

9.10 Kernel-based Function Approximation

核函数：为基于记忆的方法的样本分配权值的函数。更一般地，权值可以是基于一些其他衡量状态之间相似度的方法。

也可以理解核函数为泛化能力的度量。基于线性参数化函数逼近的泛化能力总能用核函数来表示。

核函数回归是一种基于记忆的方法，它使用所有样本计算加权平均。普通加权平均是它的一种特殊情况。

常用核函数：高斯径向基函数。Barring methods.

如果使用相同的特征向量以及相同的训练数据，采用核函数回归与线性参数化回归会得到相同的近似结果。对于可以表示为特征向量内积的核函数，其对于等价的参数化方法有着显著的优势。它支持在巨大高维特征空间中高效工作。

9.11 Looking Deeper at On-policy Learning: Interest and Emphasis

在某些场景中，我们对某些状态比对其他状态更感兴趣。通过更有目的性地利用函数逼近的资源，算法性能可以得到提升。

根据同轨策略分布进行更新。多个同轨策略分布：轨迹的初始化不同。

一个非负标量，随机变量，兴趣值 $I_t\in [0,1]$ 。兴趣值可以基于任何因果方式设定。我们现在定义 $\overline{VE}$ 中的 $\mu$ 为遵循目标政策时遇到的状态的以兴趣值为加权的分布。另一个非负标量，随机变量，强调值 $M_t$ 。它用来乘上学习过程中的更新量，因此决定了在 t 时刻强调或者不强调学习。由这两个定义我们可以得到更一般的 n 步学习法则。其中强调值由兴趣值递归地确定。

例 9.4：价值的近似值会受到参数化的约束，而使用兴趣值和强调值，可以根据我们的兴趣调整这种约束。

9.12 Summary

泛化(generalization)能力。

参数化函数逼近。均方价值误差。同轨策略分布。

随机梯度下降(SGD)。同轨策略预测。n步半梯度TD；梯度蒙特卡洛法；半梯度TD(0)。

线性函数逼近。特征。特征的选择。多项式基；傅里叶基；粗编码-瓦片编码-径向基函数。LSTD。非线性方法-ANNs。深度强化学习：一类使用非线性函数逼近方法的强化学习方法。

线性半梯度n步TD。

Bibliographical and Historical Remarks

泛化和函数逼近一直是强化学习的重要组成部分。

References

[1] Hinton, Geoffrey E., Simon Osindero, and Yee-Whye Teh. “A fast learning algorithm for deep belief nets.” Neural computation 18.7 (2006): 1527-1554.
[2] He, Kaiming, et al. “Deep residual learning for image recognition.” Proceedings of the IEEE conference on computer vision and pattern recognition. 2016.
[3] Saitoh, Koki. Deep Learning from the Basics: Python and Deep Learning: Theory and Implementation. Packt Publishing Ltd, 2021.