梯度下降算法
(一)梯度下降的原理:
梯度下降是一个一阶优化算法,又称为最速下降法。梯度下降法是最小化目标函数(假设为J(θ))的一种方法,其中θ为模型的参数,梯度下降法利用目标函数的梯度∇θJ(θ)的反方向来更新参数。学习率α 是指每次更新梯度时所指定的步长,η 的大小直接决定了函数最终会收敛于全局最小值还是局部最小值(待会儿笔者将详细介绍这里的最小值和极小值)。常见的梯度下降有三中形式,他们之间的区别在于计算目标函数梯度时用到多少数据。根据数据数量的不同,我们在参数更新的精度和更新过程的耗时不断权衡。
(二)梯度下降的数学模型
下面的h(x)是要拟合的函数,J(theta)损失函数,theta是参数,要迭代求解的值,theta求解出来了那最终要拟合的函数h(theta)就出来了。其中m是训练集的记录条数,j是参数的个数。这里J( θ)中的1/2是为了求导便利.
(三)梯度下降的三种形式
1 批梯度下降法(BDG,Batch Gradient Descent)
1,Vanilla梯度下降法,又称为批梯度下降法(batch gradient descent),在整个训练数据集上计算损失函数关于参数θ的梯度:
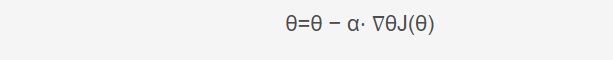 ,
,
2,因为在梯度更新的时候,我们需要再所有数据集上计算所有梯度,所以批量梯度下降算法的收敛速度会很慢,同时,批量梯度下降算法无法处理超出内存容量限制的数据集(每一个batch数据集过大),也没办法在线更新模型,即在运行的过程中无法新增样本。
批梯度下降法的代码如下所示:

3,对于给定的迭代次数,首先,我们利用全部数据集计算损失函数关于参数向量params的梯度向量params_grad。注意,最新的深度学习库中提供了自动求导的功能,可以有效地计算关于参数梯度。
4,然后,我们利用梯度的方向和学习率更新参数,学习率决定我们将以多大的步长更新参数。对于凸误差函数,批梯度下降法能够保证收敛到全局最小值,对于非凸函数,则收敛到一个局部最小值。
这里笔者需要阐述的是:
在BGD的运算过程中,我们使用的是全量样本,这是前提条件
如果目标函数本身是一个凸函数(假设为强凸函数),那么梯度下降终将收敛于目标函数的全局最小值,
众所周知,梯度下降算法是一个一阶优化算法,带入目标函数求每个点多负梯度时候,只需要求导一次,此时,我们每个点产生的拟合函数值只可能是一个极值(此时为极小值,因为负梯度)。一个函数的最小值可能是极小值,也可能不是。但由于此时目标函数为强凸函数,求导所得的点的函数值只有唯一 一个极小值,BGD又采用的是全局样本数据,所以,此时的极小值就是就是全局的最小值。如图:
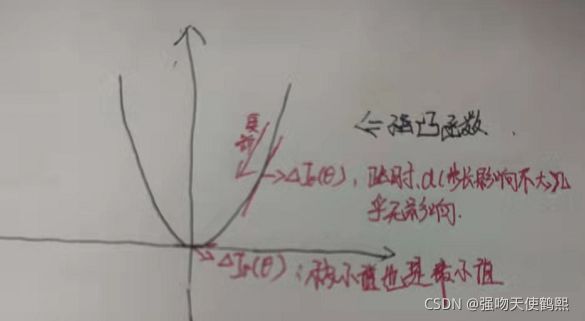
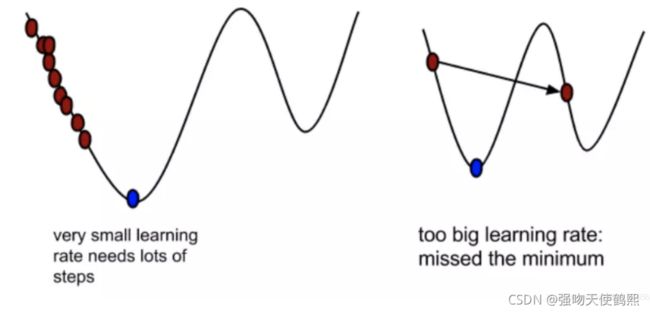
如果目标函数本身不是一个凸函数,那么梯度下降大概率将收敛于目标函数的局部最小值(步长跨过了函数最小值点,即在梯度下降没有在最小值点得到梯度。在工程实践中,一般都是收敛于局部最小值) ,当然也可能收敛于全局最小值(步长没有影响到最小值的梯度,即在一定步长下,梯度下降在最小值点取到了极值,也就是真正的最小值)。造成局部最小的主原因在于步长α,步长过大,则会错过全局极小值(也就是最终的全局最小值),步长过小,则会导致大量训练冗余。同样的计算流程,我们按照泰勒展开(也就是梯度下降的数学模型),对比全部的局部(或者全局)极小值,获得最终的局部(或全局)最小值。
2 随机梯度下降法(SDG Stochastic Gradient Descent)
1,上面的风险函数可以写成如下这种形式,损失函数对应的是训练集中每个样本的梯度,而上面批量梯度下降对应的是所有的训练样本:

每个样本的损失函数,对θ求偏导得到对应梯度,来更新θ:

其实目标函数数学模型上BGD与RGD是一样的。两者知识更行参数的方式不一样。
2,对于大数据集,因为批梯度下降法在每一个参数更新之前,会对相似的样本计算梯度,所以在计算过程中会有冗余。而SGD在每一次更新中只执行一次,从而消除了冗余。因而,通常SGD的运行速度更快,同时,可以用于在线学习。
SGD以高方差频繁地更新(在线更新算法),导致目标函数出现剧烈波动,与bdg的收敛会使得损失函数陷入局部最小值相比,由于SGD的波动,会使得目标函数跳到新的和潜在的局部最优,也就是可能会跳到全局最小值。但这个过程也会使得收敛到特定最小值的过程变得复杂,因为SGD一直在波动,就会造成大量的噪声数据,使得SGD并不是每次迭代都向着整体最优化方向进行。
然而,已经证明当我们缓慢减小学习率,SGD与批梯度下降法具有相同的收敛行为,对于非凸优化和凸优化,可以分别收敛到局部最小值和全局最小值。代码如下

3 ,对于上面的linear regression问题,与批量梯度下降对比,随机梯度下降求解的会是最优解吗?
(1)批量梯度下降—最小化所有训练样本的损失函数,使得最终求解的是全局的最优解,即求解的参数是使得经验风险最小化。
(2)随机梯度下降—最小化每条样本的损失函数,虽然不是每次迭代得到的损失函数都向着全局最优方向, 但是大的整体的方向是向全局最优解的,最终的结果往往是在全局最优解附近。即求解的参数是使得结构(泛化)风险最小化。
4,BDG和SDG的比较:
(1)梯度下降算法是批量更新算法,随机梯度下降算法是在线算法
(2)梯度下降算法优化的是经验风险最小化,而随机梯度下降优化的是泛化(结构)风险最小化
(3)梯度下降算法在损失函数非凸的情况下会陷入局部最优,而随机梯度下降算法则可以找到全局最优
(4)梯度下降算法对步长不敏感,而随机梯度算法对步长很敏感。
(5)梯度下降算法对初始点的选择敏感。而随机梯度算法不敏感。
3,小批量梯度下降算法(Mini-batch Gradient Descent)
小批量梯度下降算法综合了上述两种算法的优点,每次从训练样本集上随机抽取一个小样本集,使用抽取的样本集采用BDG的方式来更新权重参数,被抽出的小样本集所含样本点的个数称为batch_size
通常设置为2的幂次方,更有利于GPU加速处理。特别的,若batch_size=1,则变成了RDG;若batch_size=n,则变成了BDG

这种方法可以减少参数更新的方差,后期不需要逐步减小学习率也可以得到更加稳定的收敛效果,同时,作为深度学习中最常用的提督下降算法(尤其是在神经网络训练中),可以利用最新的深度学习库中高度优化的矩阵优化方法,高效地求解每个小批量数据的梯度,小批量数据的大小一般在50到256之间。

4 随机平均梯度下降算法(RVDG)
在RDG方法中,虽然避开了运算成本大的问题,但对于大数据训练而言,RDG效果常不尽如人意,因为每一轮梯度更新都完全与上一轮的数据和梯度无关。
随机平均梯度算法克服了这个问题,在内存中为每一个样本都维护一个旧的梯度,随机选择第i个样本来更新此样本的梯度,其他样本的梯度保持不变,然后求得所有梯度的平均值,进而更新了参数。
如此,每一轮更新仅需计算一个样本的梯度,计算成本等同于SG,但收敛速度快得多。
5,总结
1.批梯度下降每次更新使用了所有的训练数据,最小化损失函数,如果只有一个极小值,那么批梯度下降是考虑了训练集所有数据,是朝着最小值迭代运动的,但是缺点是如果样本值很大的话,更新速度会很慢。
2.随机梯度下降在每次更新的时候,只考虑了一个样本点,这样会大大加快训练数据,也恰好是批梯度下降的缺点,但是有可能由于训练数据的噪声点较多,那么每一次利用噪声点进行更新的过程中,就不定是朝着极小值方向更新,但是由于更新多轮,整体方向还是大致朝着极小值方向更新,又提高了速度。
3.小批量梯度下降法是为了解决批梯度下降法的训练速度慢,以及随机梯度下降法的准确性综合而来,但是这里注意,不同问题的batch是不样的
6 挑战
虽然Vanilla小批量梯度下降法并不能保证较好的收敛性,但是需要强调的是,这也给我们留下了如下的一些挑战:
1,选择一个合适的学习率可能是困难的。学习率太小会导致收敛的速度很慢,学习率太大会妨碍收敛,导致损失函数在最小值附近波动甚至偏离最小值。
2,学习率调整试图在训练的过程中通过例如退火的方法调整学习率,即根据预定义的策略或者当相邻两代之间的下降值小于某个阈值时减小学习率。然而,策略和阈值需要预先设定好,因此无法适应数据集的特点[4]。
3,此外,对所有的参数更新使用同样的学习率。如果数据是稀疏的,同时,特征的频率差异很大时,我们也许不想以同样的学习率更新所有的参数,对于出现次数较少的特征,我们对其执行更大的学习率。
4,高度非凸误差函数普遍出现在神经网络中,在优化这类函数时,另一个关键的挑战是使函数避免陷入无数次优的局部最小值。Dauphin等人[5]指出出现这种困难实际上并不是来自局部最小值,而是来自鞍点,即那些在一个维度上是递增的,而在另一个维度上是递减的。这些鞍点通常被具有相同误差的点包围,因为在任意维度上的梯度都近似为0,所以SGD很难从这些鞍点中逃开。
7, 梯度下降优化算法(拓展)
以下这些算法主要用于深度学习优化
动量法
其实动量法(SGD with monentum)就是SAG的姐妹版
SAG是对过去K次的梯度求平均值
SGD with monentum 是对过去所有的梯度求加权平均
Nesterov加速梯度下降法
类似于一个智能球,在重新遇到斜率上升时候,能够知道减速
Adagrad
让学习率使用参数
对于出现次数较少的特征,我们对其采用更大的学习率,对于出现次数较多的特征,我们对其采用较小的学习率。
Adadelta
Adadelta是Adagrad的一种扩展算法,以处理Adagrad学习速率单调递减的问题。
RMSProp
其结合了梯度平方的指数移动平均数来调节学习率的变化。
能够在不稳定(Non-Stationary)的目标函数情况下进行很好地收敛。
Adam
结合AdaGrad和RMSProp两种优化算法的优点。
是一种自适应的学习率算法
更多可参考该文章
8,梯度下降法和其他无约束优化算法的比较
在机器学习中的无约束优化算法,除了梯度下降以外,还有前面提到的最小二乘法,此外还有牛顿法和拟牛顿法。
梯度下降法和最小二乘法相比,梯度下降法需要选择步长,而最小二乘法不需要。梯度下降法是迭代求解,最小二乘法是计算解析解。如果样本量不算很大,且存在解析解,最小二乘法比起梯度下降法要有优势,计算速度很快。但是如果样本量很大,用最小二乘法由于需要求一个超级大的逆矩阵,这时就很难或者很慢才能求解解析解了,使用迭代的梯度下降法比较有优势。
梯度下降法和牛顿法/拟牛顿法相比,两者都是迭代求解,不过梯度下降法是梯度求解,而牛顿法/拟牛顿法是用二阶的海森矩阵的逆矩阵或伪逆矩阵求解。相对而言,使用牛顿法/拟牛顿法收敛更快。但是每次迭代的时间比梯度下降法长。



